2. Четность.

Опр. Функция наз. четной, если 1) симметрично относительно (0;0); 2)

Опр. Функция наз.нечетной, если 1) симметрично относительно (0;0); 2)

3. Периодичность.

Опр. Функция наз. периодической, , если : 1) ; 2)

4. ограниченность

Опр. Функция наз. ограниченной на , если - ограничена.

Опр. Функция наз. ограниченной сверху на , если - ограничена сверху, т.е.

Опр. Функция наз. ограниченной снизу на , если - ограничена снизу, т.е.

Опр. Функция наз. неограниченной , если

2. Предел и непрерывность функции в точке.

Опр.(Коши) Число в наз. пределом функции в точке а, если .

Опр.(Гейне) Число в наз. пределом функции в точке а, если .

Теорема. Если предел функции в точке сущ-ет, то он единственен.

Теорема. Если функция имеет конечный предел в точке а, то она ограничена в некоторой окрестности этой точки.

Д-во. .

ограничена .

Теорема Если на и , где

Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

1) Зам. предел:

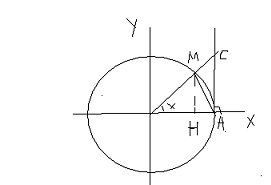
OA=1 – неподвижный радиус. ОМ – подвижный радиус. .

, , , , . , . По теореме о сжатой функции .

2) зам. предел:

3) непрерывность функции в точке.

Опр. Функция непрерывна в точке , если .

Св-ва функции непрерывной в точке.

1. Если ф. и 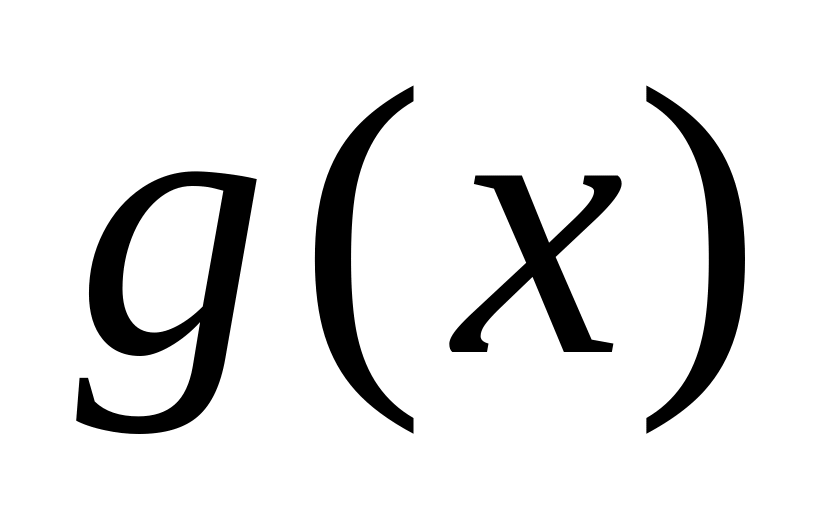непрерывны в т. , то непрер. , , ,

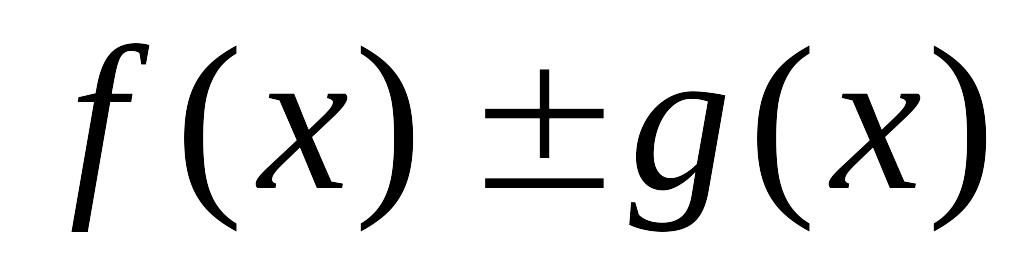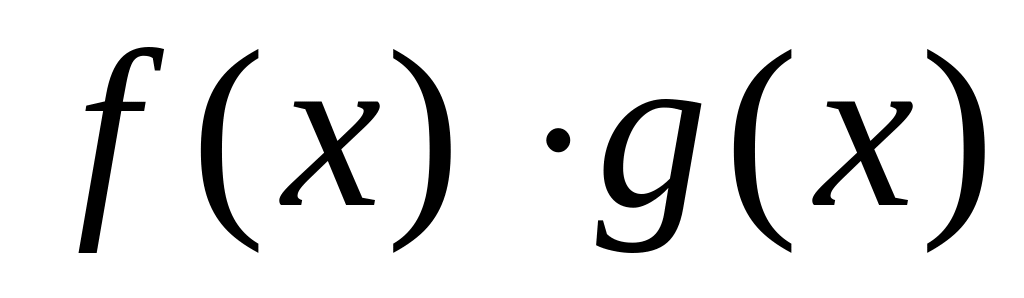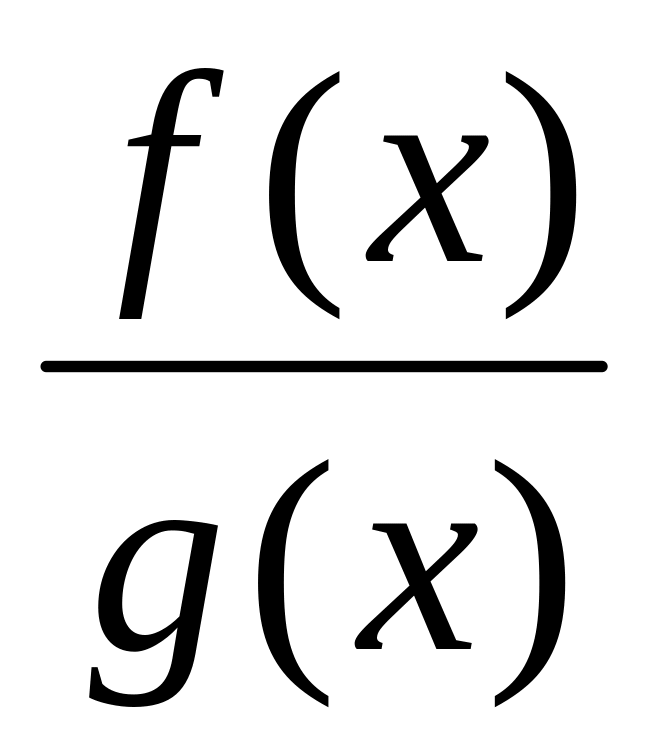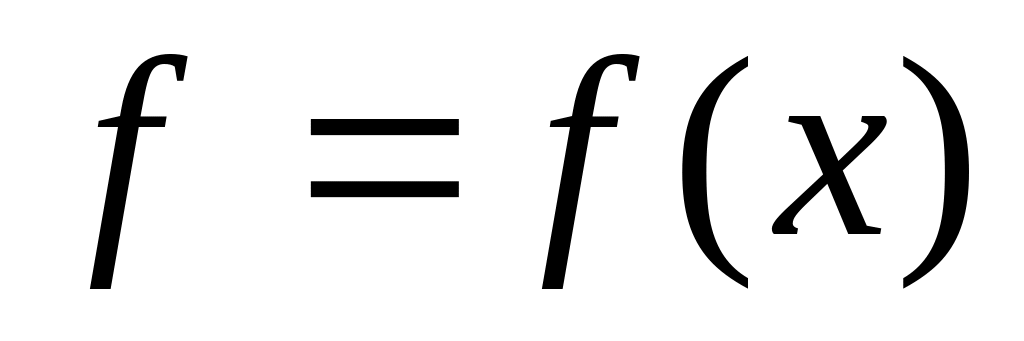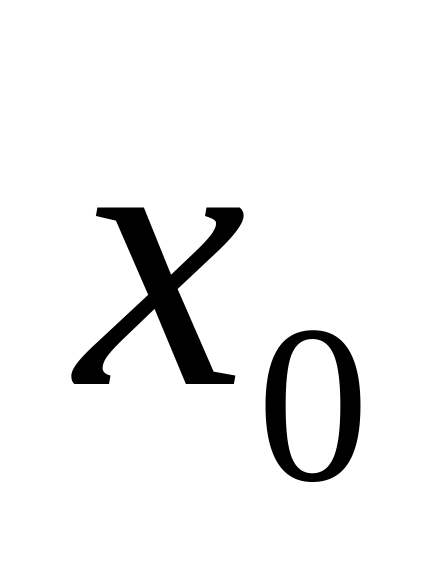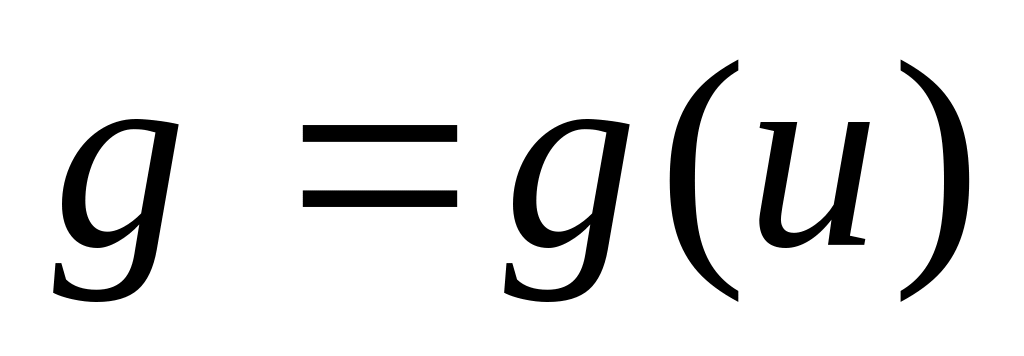2. Пусть непрер. в т. , - непрер. в т. 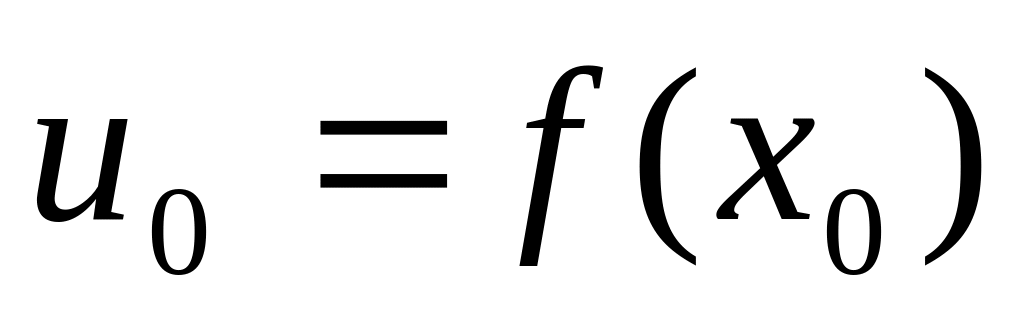, тогда композиция функций непрер. в т. .

3. Если непр. в т. , то непр. в т. и .

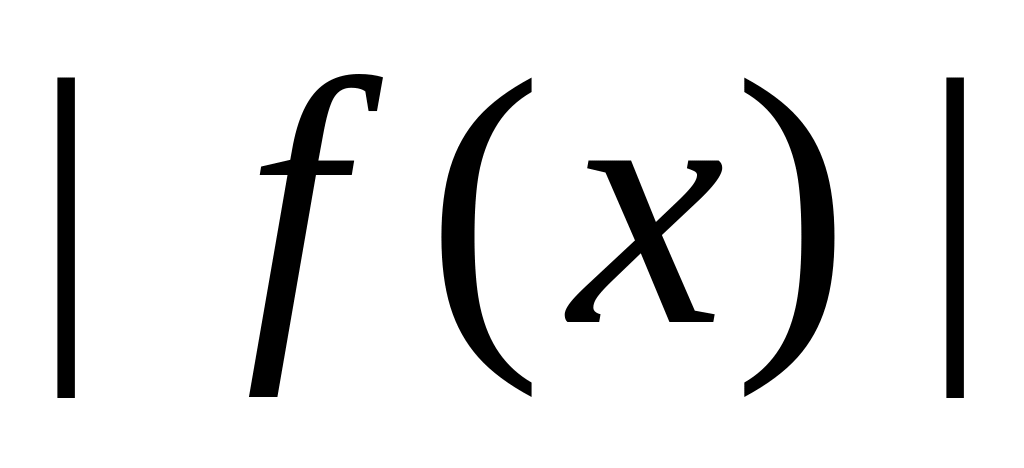Опр. Точка наз точкой разрыва , если неопределенна в т. или , если она определена в этой точке, но не явл. непрерывной в т .

Опр. Точка разрыва наз. точкой разрыва первого рода (скачком), если сущ-ет конечн. обл. одностор. предела функции в точке.

Опр. Точка 1 рода наз. устранимой точкой разрыва, если .

Опр. Точка разрыва функции наз. точкой разрыва второго рода, если хотя бы 1 из односторонних пределов функции либо конечен, либо не сущ-ет.

4. св-ва функций непрерывных на отрезке.

Опр. Функция , непрерывная в каждой точке множества, наз. непрерывной на множестве.

Теорема 2. Если функция y=f(x) строго возрастает (убывает) и непрерывна на промежутке I, то существует обратная функция x=f−1(y), которая определена на промежутке Ef=f(I) и является на Е, строго возрастающей (убывающей) и непрерывной.

Теорема (Коши) Если непрер. на [a;b], то

Теорема (Вейерштрасса) Всякая непр. на стр.ф. ограничена и достигает на этом отрезке своей верхней и нижней грани.

Опр. Функция наз. равномерно непрерывной на промежутке Х, если .

4. Непрерывность элементарных функций.

Теорема 1. Всякий многочлен непрерывен в любой точке.

Теорема 2. Всякая явл. непр. во всех точках, в которых .

Теорема 3. Показательная функция 1) , . 2) ; 3) ; 4) непрер. на всей числовой прямой.

Теорема 4. Логарифмическая функция опред. для и явл. строго возрастающей ( ), строго убывающей и непрерывной.

Теорема 5. Степенная функция непрерывна при всех .