Вопрос 1.
Множество элементов X,Y,Z… наз-ся множеством действительных чисел, если для этих элементов установлены следующие операции и отношения:
Операция сложения
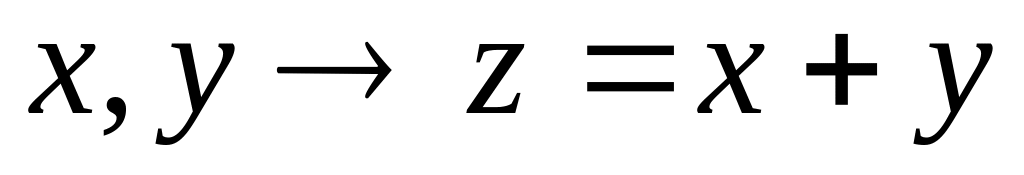
а)
б)
в)
г)
(противоположный):x+y=0
2.
Операция умножения
а)
б)
в)
г)
(обратный):xy=1
д)
3.Отношение
порядка
или
а)
;
и
,
то
б)
и
,
то
в)
,
:
г)
,
,
то
;
,
4. Аксиома о верхней грани: всякое ограниченное сверху множество обладает точной верхней гранью
Пусть множество А расположено слева от множества В. Тогда множество А ограничено сверху (любой элемент множества В является верхней границей для А), а значит, по аксиоме непрерывности, для него имеется наименьшая верхняя граница с. Это число с обладает следующим свойством: если а е Аи Ь е В, то а < с < Ъ. Значит, число с лежит как бы между множествами Аи В, разделяет эти множества. Поэтому его называют разделяющим числом.
пара (М,ρ)-метрическое пространство.
М=R, ρ(x,y)=|x-y|, (R,ρ)-пр-во действит.чисел
R2,
ρ(x,y)
.
(M,ρ)-метрич.пр-во, А подмн. М, х0єМ
Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления)
Отрицательные и нецелые (рациональные, вещественные, …) числа натуральными не являются.
Основные свойства
Коммутативность
сложения.
Коммутативность
умножения.
Ассоциативность
сложения.
Ассоциативность
умножения.
Дистрибутивность умножения относительно
сложения
Множество целых чисел
(от ср.-лат. cifra от араб. صفر
(ṣifr) «пустой,
нуль») —
,
определяется как замыкание множества
натуральных чисел
относительно арифметических операций
сложения (+) и вычитания (-). Таким образом,
сумма, разность и произведение двух
целых чисел дает снова целые числа. Оно
состоит из натуральных чисел (1, 2, 3),
чисел вида -n (
)
и числа нуль.
Q={ m/n, m-целое, n-натур }-мн-во рац.чисел
1. для любых а,в из Q имеет место хотя бы одно из трех соотношений a<b,a=b, a>b.
2. для любых a,b,c из Q, a<b, b<c, то a<c
3.
сумма, разн-ть, частное рац.чисел – число рациональное
4. между любыми рацион.числами а и b сущ-ет промежуточное число с=(a+b)/2 , a<c<b
Между любыми двумя рац.числами сущ-ет беск. мн-во рац.чисел. (Св-во плотности)
5. всякое рац.число можно представить в виде десятичной дроби.
J=R\Q (мн-во иррац. чисел)
Всякое действительное число можно представить в виде беск.десят.дроби, либо периодич., либо непериодич.
Мн-во счетно, если оно равномощно мн-ву натур-ых чисел.
Q – счетно, т.к. декартово произв. мн-в Z и N счетно.
R – не явл. счетным мн-ом.
Множество целых чисел счётно.
Мн-во чисел отрезка [0, 1] не явл. счетным
Мощностью континуума называется мощность отрезка [0, 1] c:=card[0, 1].
Мощность множества всех действительных чисел называется мощностью континуума.