
- •Необходимое условие перегиба.
- •Первое достаточное условие перегиба.
- •Второе достаточное условие перегиба.
- •Третье достаточное условие перегиба.
- •Метод замены переменной (метод подстановки)
- •Вычисление площадей плоских фигур.
- •Сходимость знакоположительных рядов
- •Признак Даламбера
- •Признак Коши
- •Линейные уравнения
- •[Править]Метод интегрирующего множителя
- •[Править]Метод вариации постоянной (метод Лагранжа)
- •18. Классическое определение вероятности.
- •19. Теоремы сложения и умножения вероятностей.
- •20.Формула полной вероятности
- •21.Формула бернулли
- •22. Дискретные и непрерывные случайные величины
- •23. Числовые характеристики дискретных случайных величин.
- •24. Задачи и основные понятия математической статистики
- •25. Статистическое распределение выборки.
- •26. Графическое изображение для выборки
- •27.Числовые характеристики для выборки и генеральной совокупности.
- •Линейная зависимость
- •Корреляционная зависимость. Коэффициент корреляции
- •Уравнение линейной регрессии
25. Статистическое распределение выборки.
Пусть изучается количественный признак Х генеральной совокупности из нее извлекается выборка объемом n при этом значение признака х1 n1; x2 n2; x3 n3;…; xk nk. Встречается значение признака nk раз.
Варианты- х1; x2; x3;…; xk ; Варианта- х1.
Частоты (числа наблюдений)- n1; n2; n3;…; nk
Относительная частота варианты = Wi=ni/n
Вариационный ряд- последовательность вариант записанных в порядке возрастания
Статистическое
распределение частот-
перечень вариант и их частот записанных
в виде таблицы

-
xi
x1
x2
…
xk
ni
n1
n2
…
nk
Статистическое
распределение относительных частот-
перечень вариант и соответствующих им
относительных частот записанных в виде
таблицы.
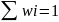
-
xi
x1
x2
…
xk
wi
w1
w2
…
wk
26. Графическое изображение для выборки
1)полигон частот- ломаная линия, отрезки которой соединяют точки с координатами
Так же и с полигоном относительных частот
В случае непрерывного признака лучше строить гистограмму, для этого интервал из значений разбивают на несколько интервалов одинаковой длинны и для каждого частичного интервала находят сумму частот вариант, попавших в данный интервал.
2)Гистограмма частот- ступенчатая фигура состоящая из прямоугольников основание которых служат частичные отрезки, а высотами отрезки длиной ni/h, где ni-число вариант попавших в данный интервал; h-длинна данного частичного интервала.
27.Числовые характеристики для выборки и генеральной совокупности.
Пусть дана ген.совокупность N
Генеральная средняя- среднее арифметическое значение генеральной совокупности.
Хг=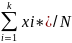
Дисперсия (
 )=
х2г-(хг)2;
х2г=
)=
х2г-(хг)2;
х2г=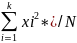
Генеральное среднее квадратическое отклонение σг=
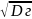
Также и для выборки
Выборочная средняя xв=
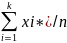
Выборочная дисперсия (
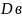 )=
х2в-(хв)2;
х2в=
)=
х2в-(хв)2;
х2в=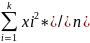
Выборочное среднее квадратическое отклонение σв=
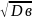
Исправленная S2=n/n-1 *
Исправленное выборочное среднее квадратическое отклонение S=
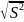
Размах варьирования R= xmax-xmin
Коэффициент вариации V= σв/ xв *100%
Мода mo- варианты с наибольшей частотой
Медиана mе- варианта которая делит вариационный ряд на 2 части равные по количеству вариант
Вопрос№ 29
ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ |
Из всех корреляционных зависимостей надо особо выделить линейную корреляцию, т.е. такую, когда точки регрессии располагаются вблизи некоторой прямой линии. В случае полной линейной корреляции приходится иметь дело с двумя видами регрессии:
1)
регрессия Y на X в виде функциональной
зависимости
2)
регрессия X на Y в виде функциональной
зависимости
Угловой
коэффициент Для определения параметров уравнения прямой линии регрессии Y на X с помощью метода наименьших квадратов получается система
в предположении, что значения X и соответствующие им значения Y наблюдались по одному разу. Запишем систему (8.1) так, чтобы она отражала данные корреляционной таблицы. Воспользуемся тождествами:
Подставив правые части тождеств в систему (8.1) и сократив обе части второго уравнения на n, получим:
Решив
эту систему, найдем параметры
Найдем
из системы (8.1) коэффициент регрессии,
учитывая, что
Умножим
обе части равенства на
Обозначим
правую часть равенства (8.4) через
Подставим
в
(8.4):
Замечание. 1. Аналогично находим выборочное уравнение прямой линии регрессии X на Y вида
где
2.
Коэффициент корреляции заключен между
–1 и 1: Если данные наблюдений над признаками X и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам:
где C1 – “ложный нуль” вариант X (новое начало отсчета): в качестве "ложного нуля" удобно принять варианту, расположенную примерно в середине вариационного ряда, имеющую наибольшую частоту; h1 – шаг, то есть разность между двумя соседними вариантами X; С2 – “ложный нуль” вариант Y; h2 – шаг вариант Y. В этом случае выборочный коэффициент корреляции
Величины
Зная эти величины, можно определить входящие в уравнения регрессии (8.5) и (8.6) величины по формулам:
|
Вопрос№ 30

 (8.1)
(8.1)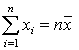 (следствие
из
(следствие
из 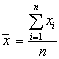 ),
),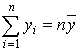 (следствие
из
(следствие
из 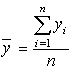 ),
), ),
),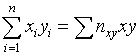 (учтено,
что пара чисел (x; y)
наблюдалась nxy раз).
(учтено,
что пара чисел (x; y)
наблюдалась nxy раз).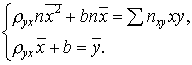 (8.2)
(8.2)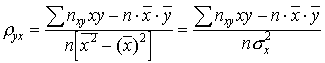 .
.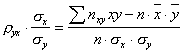 .
(8.4)
.
(8.4)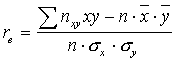 .
.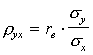 .
Подставим
.
Подставим 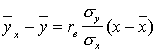 .
(8.5)
.
(8.5)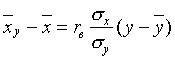 ,
(8.6)
,
(8.6) .
.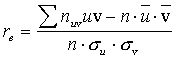 .
.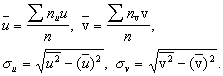
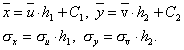 ,
,