
- •Необходимое условие перегиба.
- •Первое достаточное условие перегиба.
- •Второе достаточное условие перегиба.
- •Третье достаточное условие перегиба.
- •Метод замены переменной (метод подстановки)
- •Вычисление площадей плоских фигур.
- •Сходимость знакоположительных рядов
- •Признак Даламбера
- •Признак Коши
- •Линейные уравнения
- •[Править]Метод интегрирующего множителя
- •[Править]Метод вариации постоянной (метод Лагранжа)
- •18. Классическое определение вероятности.
- •19. Теоремы сложения и умножения вероятностей.
- •20.Формула полной вероятности
- •21.Формула бернулли
- •22. Дискретные и непрерывные случайные величины
- •23. Числовые характеристики дискретных случайных величин.
- •24. Задачи и основные понятия математической статистики
- •25. Статистическое распределение выборки.
- •26. Графическое изображение для выборки
- •27.Числовые характеристики для выборки и генеральной совокупности.
- •Линейная зависимость
- •Корреляционная зависимость. Коэффициент корреляции
- •Уравнение линейной регрессии
Сходимость знакоположительных рядов
Определение. Числовой
ряд ![]() называется
знакоположительным, если
называется
знакоположительным, если ![]() для
любого
для
любого ![]() .
.
Вопрос № 12
Признак Даламбера
Теорема (признак
Даламбера). Дан
ряд ![]() .
Пусть
.
Пусть ![]() ,
тогда
,
тогда
Если
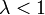 -
ряд сходится
-
ряд сходитсяЕсли
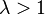 -
ряд расходится
-
ряд расходится
Признак Коши
Теорема. Дан
ряд ![]() ,
, ![]() .
Пусть
.
Пусть ![]()
тогда:
Если ряд сходится;
Если ряд расходится.
Вопрос № 13
Знакопеременные ряды. Абсолютная и условная сходимость |
|
Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда являетсязнакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки. Признак Лейбница Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть {an} является числовой последовательностью, такой, что 1. an+1 < an для
всех n;
2. Тогда
знакочередующиеся ряды Абсолютная и условная сходимость Ряд
называется абсолютно
сходящимся,
если ряд |
Пример 1 |
|
Исследовать
на сходимость ряд Решение. Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем поскольку |
Пример 2 |
|
Исследовать
на сходимость ряд Решение. Попробуем применить признак Лейбница: Видно, что модуль общего члена не стремится к нулю при n → ∞. Поэтому данный ряд расходится. |
Пример 3 |
Определить,
является ли ряд Решение. Применяя признак Даламбера к ряду, составленному из модулей соответствущих членов, находим Следовательно, данный ряд сходится абсолютно. |
Вопрос № 14
Дифференциальные уравнения первого порядка
[править]Уравнения с разделяющимися переменными
Дифференциальное
уравнение ![]() называется уравнением
с разделяющимися (отделяющимися)
переменными,
если его правая часть представима в
виде
называется уравнением
с разделяющимися (отделяющимися)
переменными,
если его правая часть представима в
виде ![]() .
Тогда, в случае
.
Тогда, в случае ![]() ,
общим решением уравнения является
,
общим решением уравнения является ![]() .
.
[править]Примеры физических задач, приводящих к уравнениям с разделяющимися переменными
[править]Охлаждение тела
Пусть ![]() —
температура тела,
—
температура тела, ![]() —
температура окружающей среды (
—
температура окружающей среды (![]() ).
Пусть
).
Пусть ![]() — количество
теплоты,
— количество
теплоты, ![]() —
удельная теплоёмкость.
Тогда количество теплоты, передаваемое
окружающей среде до выравнивания
температур, выражается формулой
—
удельная теплоёмкость.
Тогда количество теплоты, передаваемое
окружающей среде до выравнивания
температур, выражается формулой ![]() ,
или, в дифференциальной форме,
,
или, в дифференциальной форме, ![]() .
С другой стороны, скорость отдачи тепла
можно выразить в виде
.
С другой стороны, скорость отдачи тепла
можно выразить в виде ![]() ,
где
—
некий коэффициент пропорциональности.
Исключая из этих двух уравнений
,
где
—
некий коэффициент пропорциональности.
Исключая из этих двух уравнений ![]() ,
получаем уравнение с разделяющимися
переменными:
,
получаем уравнение с разделяющимися
переменными:
![]() .
.
Общим
решением этого
уравнения является семейство функций ![]() .
.

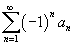 и
и  сходятся.
сходятся.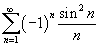 .
.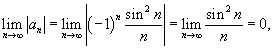
 .
.
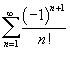 абсолютно
сходящимся, условно сходящимся или
расходящимся?
абсолютно
сходящимся, условно сходящимся или
расходящимся?