
- •Необходимое условие перегиба.
- •Первое достаточное условие перегиба.
- •Второе достаточное условие перегиба.
- •Третье достаточное условие перегиба.
- •Метод замены переменной (метод подстановки)
- •Вычисление площадей плоских фигур.
- •Сходимость знакоположительных рядов
- •Признак Даламбера
- •Признак Коши
- •Линейные уравнения
- •[Править]Метод интегрирующего множителя
- •[Править]Метод вариации постоянной (метод Лагранжа)
- •18. Классическое определение вероятности.
- •19. Теоремы сложения и умножения вероятностей.
- •20.Формула полной вероятности
- •21.Формула бернулли
- •22. Дискретные и непрерывные случайные величины
- •23. Числовые характеристики дискретных случайных величин.
- •24. Задачи и основные понятия математической статистики
- •25. Статистическое распределение выборки.
- •26. Графическое изображение для выборки
- •27.Числовые характеристики для выборки и генеральной совокупности.
- •Линейная зависимость
- •Корреляционная зависимость. Коэффициент корреляции
- •Уравнение линейной регрессии
1.Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума
Достаточное условие экстремума
1) Первое достаточное условие:
Если:
а)
f(x) непрерывная
функция
и определена в некоторой окрестности
точки![]() такой, что первая производная в
данной точке равна нулю или не существует.
такой, что первая производная в
данной точке равна нулю или не существует.
б) f(x) имеет конечную производную в окрестности задания и непрерывности функции
в)
производная сохраняет определенный
знак справа от точки
и слева от этой же точки, тогда точку
можно охарактеризовать следующим
образом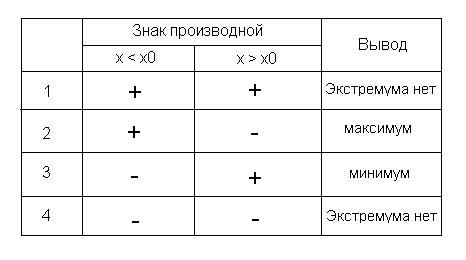
Это условие не очень удобное, так как нужно проверять множество условий и запоминать таблицу, однако если ничего не сказано о производных высших порядках, то это единственный способ найти экстремум функции.
2) Второе достаточное условие
Если
функция
g(x) обладает второй производной![]() причем в некоторой точке
первая
производная равна нулю, а вторая
производная отлично от нуля. Тогда
точка
экстремум
функции g(x),
причем если
причем в некоторой точке
первая
производная равна нулю, а вторая
производная отлично от нуля. Тогда
точка
экстремум
функции g(x),
причем если
![]() ,
то точка является максимумом; если
,
то точка является максимумом; если
![]() ,
то точка является минимумом.
,
то точка является минимумом.
3) Третье достаточное условие
Пусть функция g(x) имеет в некоторой окрестности точки N производных, причем значение первых (N - 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае:
а)
Если N - четно, то точка
экстремум
функции:![]() у функции точка максимума,
у функции точка максимума,
![]() у
функции точка минимума.
у
функции точка минимума.
б) Если N - нечетно, то в точке у функции g(x) экстремума нет.
Абсолютный экстремум
Наибольшее(наименьшее) значение на сегменте [a;b] непрерывной функции g(x) достигается или в критической точке этой функции(т.е. где производная равна нулю или не существует), или в граничных точках а и b данного сегмента.
2.


3. Точка
![]() называется
точкой
перегиба графика функции
y=f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки
называется
точкой
перегиба графика функции
y=f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки
![]() ,
в пределах которой слева и справа от
точки М
график функции имеет разные направления
выпуклости.
,
в пределах которой слева и справа от
точки М
график функции имеет разные направления
выпуклости.
Необходимое условие перегиба.
Сформулируем необходимое условие перегиба графика функции.
Пусть график
функции y=f(x)
имеет перегиб в точке
и
имеет при
![]() непрерывную
вторую производную, тогда выполняется
равенство
непрерывную
вторую производную, тогда выполняется
равенство
![]() .
.
Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения , в которых вторая производная равна нулю, являются абсциссами точек перегиба.
Еще следует
обратить внимание, что по определению
точки перегиба требуется существование
касательной прямой, можно и вертикальной.
Что это означает? А означает это следующее:
абсциссами точек перегиба могут быть
все
из
области определения функции, для которых
![]() и
и
![]() .
Обычно это точки, в которых знаменатель
первой производной обращается в ноль.
.
Обычно это точки, в которых знаменатель
первой производной обращается в ноль.
Первое достаточное условие перегиба.
После того как найдены все , которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции.
Пусть функция y=f(x) непрерывна в точке , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки . Тогда, если в пределах этой окрестности слева и справа от , вторая производная имеет разные знаки, то является точкой перегиба графика функции.
Как видите первое достаточное условие не требует существования второй производной в самой точке , но требует ее существование в окрестности точки .
Второе достаточное условие перегиба.
Если
,
а
![]() ,
тогда
является
абсциссой точки перегиба графика функции
y=f(x).
,
тогда
является
абсциссой точки перегиба графика функции
y=f(x).
Третье достаточное условие перегиба.
Пусть
![]() ,
а
,
а
![]() ,
тогда если n
– четное число, то
является
абсциссой точки перегиба графика функции
y=f(x).
,
тогда если n
– четное число, то
является
абсциссой точки перегиба графика функции
y=f(x).
4. График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
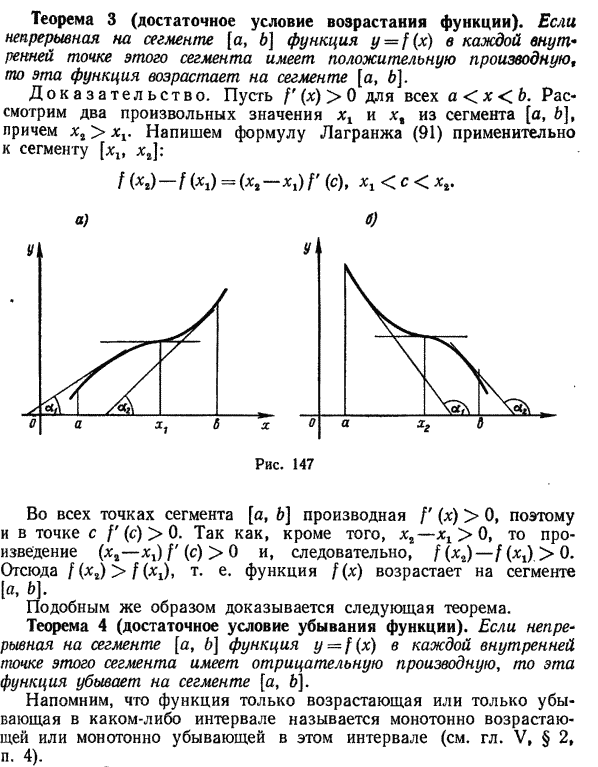
Достаточное условие
Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем
на графике функции y
= f(x) произвольную
точку M0
с абсциссой x0
Î (a;
b)
и проведем через точку M0
касательную. Ее уравнение
![]() .
Мы должны показать, что график функции
на (a; b)
лежит ниже этой касательной, т.е. при
одном и том же значении x
ордината кривой y
= f(x) будет
меньше ордината касательной.
.
Мы должны показать, что график функции
на (a; b)
лежит ниже этой касательной, т.е. при
одном и том же значении x
ордината кривой y
= f(x) будет
меньше ордината касательной.
5.Асимптоты
графика функции.
ОПР. Прямая
![]() называется
вертикальной асимптотой графика функции
называется
вертикальной асимптотой графика функции
![]() ,
если функция является бесконечно большой
в точке
.
,
если функция является бесконечно большой
в точке
.
ОПР.
Прямая
![]() называется
горизонтальной асимптотой графика
функции
на
бесконечности, если
называется
горизонтальной асимптотой графика
функции
на
бесконечности, если
![]() .
.
ОПР.
Прямая
![]() называется
наклонной асимптотой графика функции
на
бесконечности, если
называется
наклонной асимптотой графика функции
на
бесконечности, если
![]() .
.
ТЕОРЕМА
5. Если график функции
имеет
прямую
своей
наклонной асимптотой, то
![]() ,
,
![]() .
ДОК.
По условию
.
ДОК.
По условию
![]() ,
где
,
где
![]() -
бесконечно малая функция на бесконечности
и
-
бесконечно малая функция на бесконечности
и
![]() .
Поскольку
.
Поскольку
![]() -
бесконечно малая функция на бесконечности,
то
.
По условию
-
бесконечно малая функция на бесконечности,
то
.
По условию
![]() и
по теореме
.
ТЕОРЕМА
6. Если для функции
существуют
пределы
и
,
то прямая
является
наклонной асимптотой ее графика.
ДОК.
По условию
и
по теореме
.
ТЕОРЕМА
6. Если для функции
существуют
пределы
и
,
то прямая
является
наклонной асимптотой ее графика.
ДОК.
По условию
![]() .
Тогда
.
Тогда
![]()
6.Свойства первообразной и неопределенного интеграла.
Определение первообразной.
Первообразной
функции f(x)
на промежутке (a;
b)
называется такая функция F(x),
что выполняется равенство
![]() для
любого х
из заданного промежутка.
для
любого х
из заданного промежутка.
Если
принять во внимание тот факт, что
производная от константы С
равна нулю, то справедливо равенство
![]() .
Таким образом, функция f(x)
имеет множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
.
Таким образом, функция f(x)
имеет множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение неопределенного интеграла.
Все
множество первообразных функции f(x)
называется неопределенным интегралом
этой функции и обозначается
![]() .
.
Выражение
![]() называют
подынтегральным
выражением,
а f(x)
– подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
называют
подынтегральным
выражением,
а f(x)
– подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
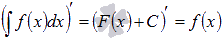 Производная
результата интегрирования равна
подынтегральной функции.
Производная
результата интегрирования равна
подынтегральной функции.
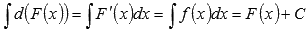 Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
 ,
где k
– произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
,
где k
– произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
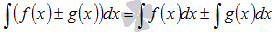 Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для
доказательства третьего и четвертого
свойств достаточно найти производные
от правых частей равенств:
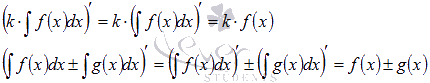
Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
7. Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. Таблица интегралов.
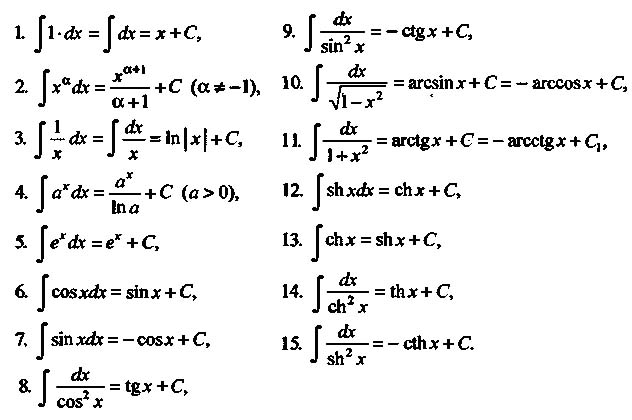
Интегрирование по частям — применение следующей формулы для интегрирования:
![]()
Или:
![]()
В частности, с помощью n-кратного применения этой формулы находится интеграл
![]()
где
![]() —
многочлен
—
многочлен
![]() -ой
степени.
-ой
степени.
