Необоротні процеси

Як було зазначено, оборотні процеси протікають послідовно через ряд станів рівноваги. Самовільний же плин процесу завжди пов'язаний з його необоротністю. Необоротними в термодинамічному змісті називаються такі процеси, після протікання яких систему вже не можна повернути в початковий стан без того, щоб не залишилося яких-небудь змін у ній самій або в навколишнім середовищі. Так, перехід теплоти від більше гарячого тіла до більш холодного є процесом необоротним, і не можна провести його у зворотному напрямку, не затрачуючи на це роботи.

Для деяких простих необоротних процесів легко показати, що в ізольованих системах плин їх супроводжується зростанням ентропії системи. Покажемо, наприклад, що перехід теплоти від гарячого тіла до холодного супроводжується зростанням ентропії.

Можна показати, що й перехід газу з посудини з більшим тиском у посудину з меншим тиском і інші необоротні процеси при протіканні їх в ізольованих системах завжди супроводжуються зростанням ентропії системи.

Другий закон термодинаміки встановлює, що в будь-якому циклі, що включає необоротні процеси

Із цього аж ніяк не витікає, що зміна ентропії в циклі, що включає необоротні процеси, не дорівнює нулю. Ентропія є функцією стану, і зміна її не залежить від умов проведення процесу й, зокрема, від його оборотності. Якщо система повернулася у вихідний стан, а це є умовою кругового процесу, то її ентропія завжди приймає вихідне значення, і, отже, зміна ентропії дорівнює нулю. Але теплота процесу залежить від умов його проведення, і нерівність означає, що при необоротному процесі буде справедливою нерівність

Ентропія й термодинамічна ймовірність системи

Установлення статистичної природи другого закону дало можливість Больцману (1896) визначити статистичний зміст ентропії.

Можна показати, що

де k — постійна Больцмана W - термодинамічна ймовірність даного стану системи.

Це важливе співвідношення лежить в основі сучасної статистичної термодинаміки.

Про рівновагу

Рівноважним станом називається такий термодинамічний стан системи, що не змінюється в часі, причому ця незмінюваність не обумовлена протіканням якого-небудь зовнішнього процесу.

Положення рівноваги завжди залежить від зовнішніх умов. Тому що зовнішні умови не можуть зберігатися постійно незмінними, отже, рівновага рано або пізно зміщується або порушується. Існують різні види рівноважних станів. Ми зупинимося тут переважно на найважливішому для нашого курсу — стійкій рівновазі.

При стійкій рівновазі будь-які стани, суміжні з ним, є менш стійкими, і перехід до них зі стану стійкої рівноваги завжди пов'язаний з необхідністю витрати роботи ззовні.

При стійкій рівновазі всякий нескінченно малий вплив викликає тільки нескінченно малі зміни в стані системи. Він не може викликати плину необоротних процесів. По припиненні такого впливу система прагне знову відновити колишній стан.

Статистична механіка показує, що

рівноважний стан, до якого, відповідно до другого початку, як до межі прагне всяка термодинамічна система, є станом, найбільш імовірним у даних умовах у порівнянні з будь-яким суміжним з ним станом.

Стійка рівновага є динамічною за характером. Рівноважний стан зберігається в часі не внаслідок відсутності або припинення процесу, а внаслідок протікання його одночасно у двох протилежних напрямках з однаковою швидкістю. Саме рівність швидкостей прямого й зворотного процесів є причиною збереження системи без зміни в часі (при незмінності зовнішніх умов).

Наприклад, при випаровуванні рідини, при постійних зовнішніх умовах, число молекул, що вилітають із рідини в одиницю часу з даної поверхні, постійно. Число ж молекул, що конденсуються назад з пари в рідину, залежить від концентрації пари, що збільшується в міру випару.

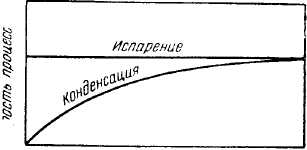
Час —-

Рис.1. Досягнення рівноваги при випаруванні рідини.

З підвищенням концентрації пари швидкість зворотного процесу наближається до швидкості прямого процесу (рис 1.). Коли обидві швидкості стануть рівними, установиться рівновага. При стійкій рівновазі між рідиною і її парою число молекул, що вилітають із рідини в пару, дорівнює числу молекул, що конденсуються з пари в рідину за той же проміжок часу.

Перейдемо тепер до питання про різний ступінь стійкості станів рівноваги.

Ступінь стійкості різних станів у фізико-хімічних системах може бути досить різною. Стан, якому відповідає невелика відносна стійкість, називають метаcтабільним. Звичайними прикладами метастабільних станів можуть служити стан пересиченої пари, пересиченого розчину, переохолодженої рідини й т.д. Перехід у більше стійкі стани може бути викликані у цих системах досить слабкими впливами. Так, можна викликати кристалізацію розчиненої речовини з пересиченого розчину, якщо внести в розчин невеликий кристалик розчиненої речовини.

Нерідко стани, відносно мало стійкі в термодинамічному сенсі, практично довгостроково зберігаються в часі, що дає можливість застосовувати речовини в таких станах. Так, окисли заліза є більше стійкими у звичайних умовах у присутності кисню, чим металеве залізо. Однак це не заважає широко застосовувати металеве залізо в атмосферних умовах, хоча при цьому й відбувається деяка втрата заліза (іржавіння).

Також і вуглекислий газ у звичайних умовах є більше стійким, чим вугілля або графит. Однак це не перешкоджає їхньому застосуванню в присутності кисню, хоча за певних умов може відбутися самозаймання вугілля.

Не слід думати, що якщо можливі різні напрямки зміни даної речовини й утворення продуктів, різних за стійкістю, то переважати завжди буде той напрямок, який веде до найбільш стійкого стану. Тий або інший напрямок процесу визначається в першу чергу співвідношенням швидкостей паралельних процесів, а в більшості випадків швидкість залежить не стільки від термодинамічних параметрів процесу, скільки від кінетичних факторів.