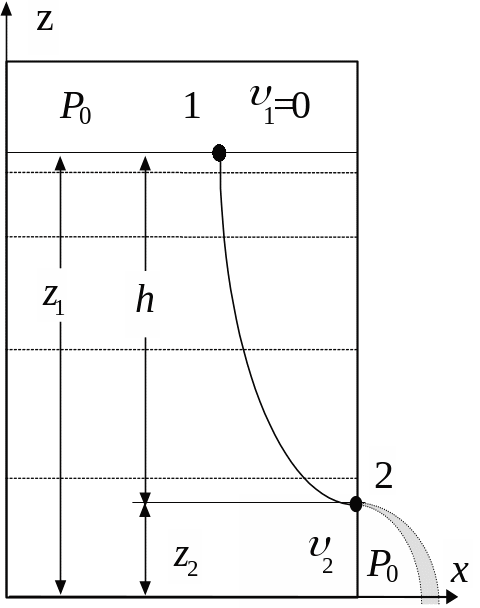
7.2.3. Скорость истечения идеальной несжимаемой жидкости из сосуда
Уравнение Бернулли имеет самое
широкое применение на практике.
Рассмотрим несколько примеров. В
качестве первого примера рассмотрим
стационарное истечение идеальной
несжимаемой жидкости из сосуда (рис.7.1).
Если полагать, что сосуд достаточно
велик, а отверстие мало, то можно считать,
что при истечении уровень жидкости не
изменяется заметно в течение достаточно
продолжительного промежутка времени.
Пусть на поверхность жидкости в сосуде
действует давление
(например, атмосферное). Будем также
полагать, что струя вытекает в
пространство, где внешнее давление
также равно
(истечение в атмосферу). Обобщение на
различные давления не составляет труда.
Проведем некоторую гипотетическую
линию тока и выберем на ней две точки:
одну на поверхности жидкости в сосуде
(точка 1), другую внутри отверстия (точка
2).
Рис.7.1 |
Тогда для этой линии тока можно записать уравнение Бернулли (7.2.7):
Поскольку
поверхность жидкости в сосуде
предполагается неподвижной
Заметим, что такую же скорость приобретает тело, которое падает в пустоте с высоты h.
|
),
из последнего равенства следует:
(7.2.9)
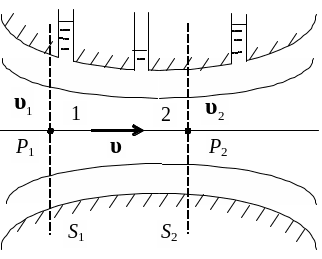
7.2.4. Распределение давления в трубе переменного сечения
Рассмотрим стационарное движение идеальной несжимаемой жидкости в трубе переменного сечения, направленное слева направо на Рис.7.2. Действием силы тяжести можно пренебречь. Выберем какую - либо линию тока (например, осевую). На этой линии тока рассмотрим две произвольные точки 1 и 2. Тогда для этих точек на выбранной линии тока можно записать в
Рис.7.2
|
соответствии с уравнением Бернулли:
Из данного уравнения следует, что в той точке на линии тока, где скорость больше, гидростатическое давление меньше и наоборот. Непрерывность движения жидкости в трубе требует выполнения следующего закона:
Данный закон называют также условием не накопления вещества или |
(7.2.10)
(7.2.11)условием не разрывности струи в любом сечении трубы. В соответствии с этим законом поток массы при движении идеальной жидкости в трубе переменного сечения есть величина постоянная. Из этого условия следует, что скорость несжимаемой жидкости тем больше, чем меньше сечение трубы, и она максимальна в самом узком сечении трубы. Следовательно, в самом узком месте трубы давление минимально согласно (7.2.9). Если на поверхности трубы установить манометрические трубки, то жидкость в них будет находиться на разных уровнях. Самый низкий уровень манометрической жидкости, следовательно, будет в самом узком сечении трубы.
В качестве примеров, которые могут быть просто объяснены при помощи установленного вывода, можно привести следующие. Например, капитанам судов запрещается проводить сближение судов, идущих параллельным курсом, до некоторого минимального расстояния. Действительно, при этом вода между двумя судами приобретает некоторую дополнительную скорость за счёт сужения канала, образованного бортами судов, а давление воды между судами оказывается меньшим, чем вне них. Поэтому возникают силы, равные разности сил давлений на внешние и внутренние борта судов и стремящиеся сблизить суда, что может привести к их столкновению (рис.7.3а). Хорошо известен экспериментальный факт, что, если продувать воздух между двумя параллельными листами бумаги, то они будут стремиться сблизиться (рис.7.3б).
Рис.7.3
При сильных и порывистых ветрах иногда наблюдается непривычное на первый взгляд явление. Крыша дома вместе с верхним венцом бревен поднимается вверх, а затем уже опрокидывается ветром. Нетрудно понять, почему это происходит. Если перед порывом ветра давление снаружи крыши и на чердаке дома уравниваются, то при резком порыве ветра над крышей создаётся меньшее давление, чем на чердаке, и если через щели между крышей и последним венцом коробки дома эта разность давления не успеет выровняться. Крышу поднимет создавшаяся значительная результирующая сила, направленная вверх и равная произведению разности давления на площадь, а затем ветром крыша сбрасывается с дома (рис.7.3г).