7.11.3.3. Этапы вычислительного цикла

Расчетная программа содержит следующие этапы:

1. Задаются начальные условия (как правило, в невозмущенный поток газа мгновенно помещается тело).

2. Аппроксимируются параметры потока в приграничных ячейках (на свободной границе). Причем, с одной стороны, значения параметров внутри зоны известны, а, с другой, известны условия набегающего потока.

3. Для каждой ячейки внутри расчетной зоны вычисляются плотности потоков через каждую площадку. Здесь следует учитывать условия на границе с телом, это осуществляется за счет задания потоков импульса (и энергии, в общем случае) через площадку, примыкающую к твердому телу.

4. Для каждой ячейки, зная плотности потоков, умножая их на шаг по времени и на соответствующую площадь (в двумерном случае длину) и суммируя по всем границам, вычисляется изменение соответствующих количеств (массы, компонент импульса и т.д.).

5. По известному изменению количеств за временной шаг, пересчитывается масса, импульс и, если необходимо, энергия газа в каждой ячейке.

6. Пункты 2-5 повторяются до тех пор, пока по какому-либо критерию не будет принято решение, что расчет закончен.

Блок схема алгоритма расчета приведена на рис. 7.28.

При организации граничных условий газ – твердое тело необходимо модифицировать расчетные формулы (7.11.14). Это связано с тем, что при расчете плотности в приграничной ячейке в формуле (7.11.14) для этой ячейки могут использоваться плотности газа в ячейках, которые находятся внутри твердого тела, а для них плотность газа не определена. Поэтому, например, в случае ячейки, граничной с твердым телом, которое прилегает к стороне и в случае, если плотность на определяется по формуле:

. (7.11.17)

Кроме того, для организации условия непротекания необходимо задавать нулевые плотности потока импульса через границу газ – твердое тело.

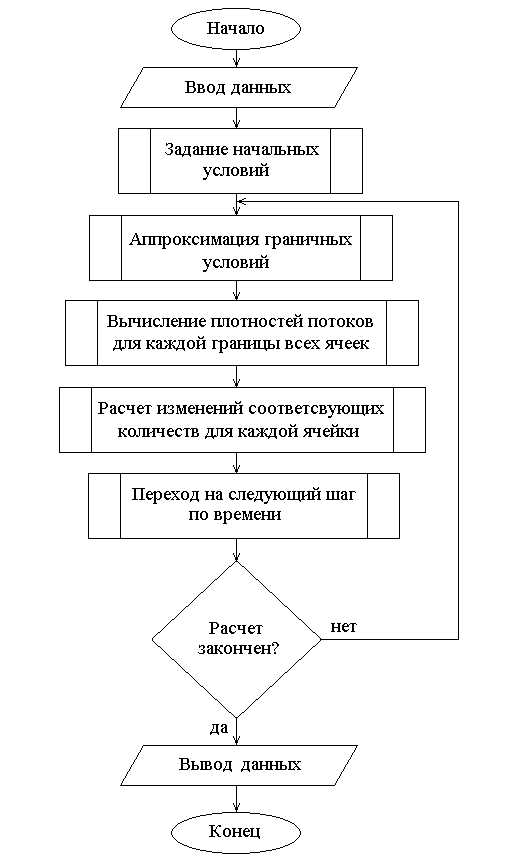
Рис. 7.28. Блок-схема алгоритма программы расчета внешнего обтекания

7.11.4. Результаты расчета

В двух численных экспериментах использовались геометрические параметры расчетной зоны, приведенные в таблицt 7.1, а в таблице 7.1 – параметры газового потока гексафторида урана.

Таблица 7.1

Параметры расчетной области при обтекании прямоугольного выступа эйлеровым газом

№ эксперимента	, м	, м	, м	, м	, м	, м	, м
1	3	1,5	0,03	0,05	0,45	0,75	0,6
2	5	1,5	0,025	0,05	0,375	0,75	2,5

Таблица 4.2

Параметры газа при обтекании прямоугольного выступа эйлеровым газом

№ эксперимента	, Па	, м/с	, кг/м3	, К	, кг/моль
1	1333	1	0,188	300	0,352
2	1333	200 ( 2)	0,188	300	0,352

На рис. 7.29 приведено полученное в численном эксперименте № 1 поле скоростей, а на рис. 7.30 – поле давления. При обтекании выступа эйлеровым газом при заданных условиях образуется две зоны циркуляции: сверху над выступом и справа от выступа. На рис. 7.30 можно видеть, что в тех местах, где возникают зоны циркуляции потока (рис. 7.29), давление заметно уменьшается. И напротив, слева от выступа, где поток набегающего газа «упирается» в стенку, давление возрастает.

В увеличенном масштабе эти зоны вихревого движения изображены над выступом на рис. 7.31, а за выступом на рис.7.32. Как видно на рис. 7.31, в отсутствии сил вязкости вблизи твердой стенки над выступом поток гексафторида урана циркулирует в двух вихрях: по набегающему потоку в передней части по часовой стрелке и против направления набегающего потока в задней части против часовой стрелки, в которую наблюдается заброс среды из глобального вихря за выступом, как видно на рис. 7.31 и 7.32.

Рис. 7.29. Распределение скоростей индивидуальных частиц

в расчетной области (эксперимент № 1)

Рис. 7. 30. Распределение давления в расчетной области

(эксперимент № 1)

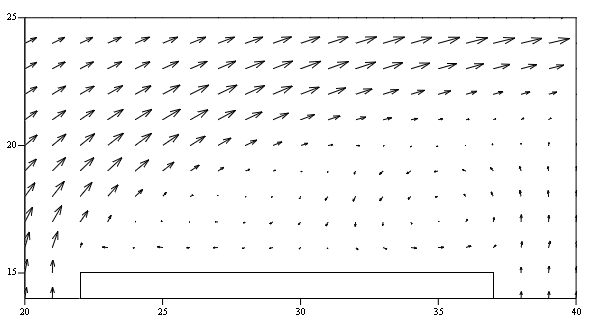
Рис. 7.31. Поле скоростей над верхней поверхностью выступа

(эксперимент № 1)

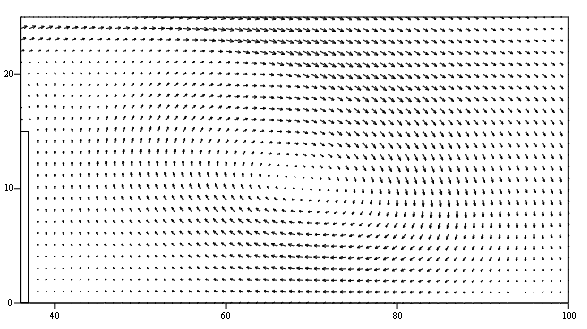
Рис. 7.32. Глобальный вихрь за выступом

При обтекании прямоугольного выступа сверхзвуковым потоком газа (эксперимент №2 в табл. 7.1, 7.2) образуется ударная волна перед выступом (рис 7.33 и 7.34). На рисунках видно, что перед пластинкой образуется ударная волна, давление в которой почти в 5 раз превышает давление в набегающем потоке, а за пластинкой образуется обширная разреженная зона, давление в которой в 1.5 раза меньше давления в набегающем потоке.

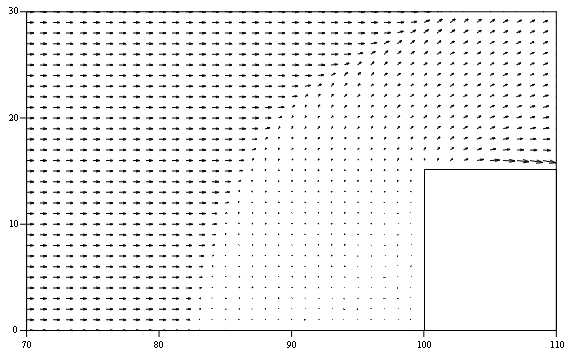
Рис. 7.33. Поле скоростей перед выступом (эксперимент № 2)

Рис. 7.34. Ударная волна в сверхзвуковом потоке идеального газа

при обтекании выступа (эксперимент № 2)

Таким образом, при обтекании выступа сверхзвуковым потоком идеального газа перед ним возникает ударная волна – скачок уплотнения плотности. Во фронтальной и кормовой областях поля течения возникает разность давлений, которая тем больше, чем выше скорость набегающего потока. Эта разность давлений является источником возрастания энтропии в сверхзвуковом потоке идеального газа.