7.7. Суперпозиция потенциальных потоков

7.7.1. Обтекание бесконечного цилиндра с циркуляцией

При потенциальном движении идеальной, несжимаемой среды потенциал скорости должен удовлетворять уравнению Лапласа (7.5.7)

Уравнение Лапласа является линейным уравнением относительно потенциала скорости . Следовательно, сумма любых его решений также является его решением. Поэтому, суммируя известные простейшие решения уравнения Лапласа, можно получить решения, имеющие во многих случаях вполне реальный смысл и практическое значение. Очевидно:

(7.7.1)

Таким образом, скорость сложного движения определяется суммой векторов скоростей простых движений.

Наложим на потенциальное движение среды со скоростью при обтекании цилиндра плоский вихрь с интенсивностью (или циркуляцией) , вращающийся против часовой стрелки

(7.7.2)

Суммируя согласно (7.7.1) скорости простых движений, получим скорость сложного движения с компонентами, которые с учетом (7.6.9), (7.7.1) и (7.7.2) равны:

(7.7.3)

Для построения линий тока найдем положение критических точек на поверхности цилиндра при . В критических точках А и В на поверхности цилиндра (см. рис. 7.18). Следовательно, должны обращаться в нуль как , так и компоненты скорости . Радиальная компонента скорости на поверхности цилиндра в любой точке равна нулю. Касательная же компонента скорости равна нулю в точках, определяемых соотношением (7.7.3) для , т.е.

(7.7.4)

Возможны следующие случаи:

1. Если (обтекание цилиндра без циркуляции), то имеет место прежний результат (см. п. 7.6.4) и

2. Если , то критические точки А и В находятся на верхней половине поверхности цилиндра, т.к. лежит в пределах

3. Если , то обе точки сливаются в одну при .

4. При не существует при , и критических точек на поверхности цилиндра не существует; они могут быть расположены только в поле течения среды..

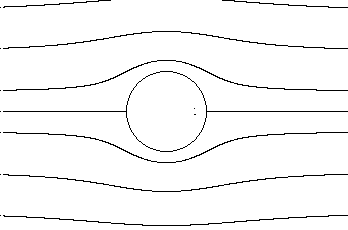
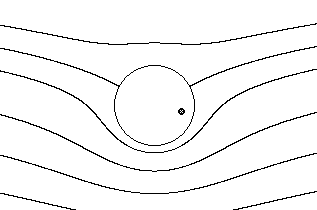
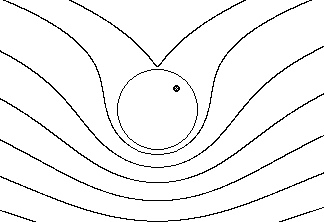
Картина линий тока для этих случаев представлена на рис. 7.20а, б, в, г .

7.7.2. Распределение давления. Подъемная сила

Вычислим результирующие силы, действующие со стороны среды на единицу длины поверхности цилиндра при обтекании его потоком идеальной среды с циркуляцией. Для этого найдём распределение давления по поверхности цилиндра в соответствии с первым уравнением (7.6.12), имея ввиду, что при r = r₀ и :

(7.7.5)

а). Г = 0	б).
в).	г).

Рис. 7.20

Подставляя в (7.6.19) скорость на поверхности цилиндра (7.6.17), получим:

(7.7.6)

Силу сопротивления и подъёмную силу возможно вычислить согласно (7.6.13) и (7.6.14):

(7.7.7)

После подстановки (7.7.6) в (7.7.7) и интегрировании по углу в пределах от до следует:

(7.7.8)

Как и прежде, для силы лобового сопротивления имеет место парадокс Даламбера, т.е. . Однако циркуляция стимулирует возникновение подъёмной силы, которая направлена в сторону, противоположную направлению оси y (рис. 7.20), и равна

(7.7.9)

7.7.3. Эффект Магнуса

При , как и в предыдущей задаче, подъёмная сила исчезает. Возникновение подъемной силы при обтекании цилиндра с циркуляцией называют эффектом Магнуса. Эффект Магнуса является частным случаем общей теоремы известного русского гидродинамика Н.Е.Жуковского о подъёмной силе крыла. Согласно теореме Жуковского для вычисления подъёмной силы крыла при обтекании его реальной средой необходимо вычислить лишь циркуляцию скорости вокруг крыла. Жуковским, а затем его учеником академиком С.А.Чаплыгиным были разработаны специальные методы вычисления такой циркуляции при разрывных течениях среды около крыла.

Происхождение подъёмной силы при обтекании цилиндра с циркуляцией легко понять, если обратиться к уравнению Бернулли (7.6.11). Как видно на

рис 7.20, в верхней части поля течения скорость обтекания цилиндра плоским потоком и циркуляционная скорость (например, при θ = π/2) вычитаются, а в нижней (при θ = 3π/2) - складываются. Поэтому результирующая скорость суммарного движения в верхней половине цилиндра оказывается меньше, чем в нижней. Из уравнения же Бернулли следует, что действующее на верхнюю половину цилиндра давление, больше, чем на нижнюю. В результате (см. 7.7.8) возникает результирующая подъемная сила, направленная вниз (рис. 7.20).

Жуковским было предложено простое правило определения направления действия главного вектора сил давления на поверхность цилиндра:

- поместить вектор скорости набегающего потока при обращенном движении в центр неподвижного цилиндра, повернуть его на 90⁰ в сторону, противоположную скорости циркуляционного движения; это и даст направление главного вектора F .

Приведём несколько примеров, демонстрирующих эффект Магнуса. Если легкий бумажный цилиндр скатывается с наклонной поверхности стола (рис.7.21а), то его вращение при падении со стола существенно изменяет траекторию движения. Если без вращения его траектория описывалась бы кривой 1, то вращение делает траекторию более крутой. Действительно, при движении цилиндра по наклонной плоскости после отрыва вблизи поверхности цилиндра за счёт сил вязкости реального газа образуется вращающийся по часовой стрелке приповерхностный слой, в котором индивидуальные частицы участвуют в сложном поступательно-вращательном движении. Это сложное движение в соответствии с законом суперпозиции может быть представлено в виде суммы двух простейших движений идеального газа: плоского поступательного и вращательного с постоянной циркуляцией. Поэтому в верхнем полупространстве над цилиндром скорости двух движений вычитаются и согласно уравнению Бернулли здесь давление больше, а в нижнем - складываются и давление меньше. В результате возникает результирующая подъёмная сила, которая в соответствии с правилом Жуковского делает траекторию цилиндра более крутой.

а) б) в)

Рис. 7.21

Известно, что должным образом закрученные шарик пинг-понга, теннисный, волейбольный и футбольный мячи могут описывать довольно сложные траектории. Так, например, чтобы траектория шарика пинг-понга над столом была круче, то игроку при не сильной подаче необходимо закрутить его по часовой стрелке (рис. 7.21б). Возникающая в этом случае подъёмная сила «прогнёт» траекторию полёта вниз и шарик, достигнув апогея над сеткой на другой площадке, при падении вниз будет двигаться по более крутой траектории, чем без закрутки. При сильной подаче теннисного мяча профессионалом и закрутке его против часовой стрелки противнику кажется, что мяч ударится в сетку. Однако возникающая подъёмная сила «поднимет» мяч над сеткой и сделает траекторию более пологой с крутым падением его в конце площадки. Аналогичного эффекта добиваются и футболисты-профессионалы при подаче крученых штрафных мячей, огибающих стенку из футболистов-соперников перед воротами.

В 1924 г. английским ученым Флеттнером было сконструировано и построено роторное судно, использующее рассматриваемый эффект. На судне были установлены два легких, обтянутых парусиной цилиндра, которые приводились во вращение моторами. Диаметр цилиндров был 2.8 м, высота 18 м. Такое судно развивало скорость около 15 км/час. Причем естественно, что максимальная скорость развивалась при боковом ветре, когда «подъемная» сила направлена вдоль корпуса судна от кормы к носовой части. Однако это изобретение не получило своего дальнейшего развития в связи с быстрым строительством дизельных двигателей. Эффект Магнуса является также одной из причин отклонения траектории вращающегося снаряда из вертикальной плоскости, проходящей через ось ствола орудия (явление деривации).

Снова обратим внимание на то, что в идеальной среде, лишённой трения, нельзя, вращая цилиндр, создать в ней вращательное движение. Только благодаря вязкости реальной среды вращающийся цилиндр создает вокруг себя вращательное движение, которое вдали от тела можно считать потенциальным. Отвлекаясь от причин, создавших вращательное потенциальное движение, удаётся в рамках модели идеальной среды рассмотреть и объяснить многие явления, наблюдаемые в реальных средах.

Рассмотренный метод суперпозиции потенциальных потоков, как и метод конформных отображений, позволяет составлять из известных простейших движений идеальной среды такие движения, которые были бы близки по свойствам к движениям среды в реальных задачах, имеющих практическое значение.