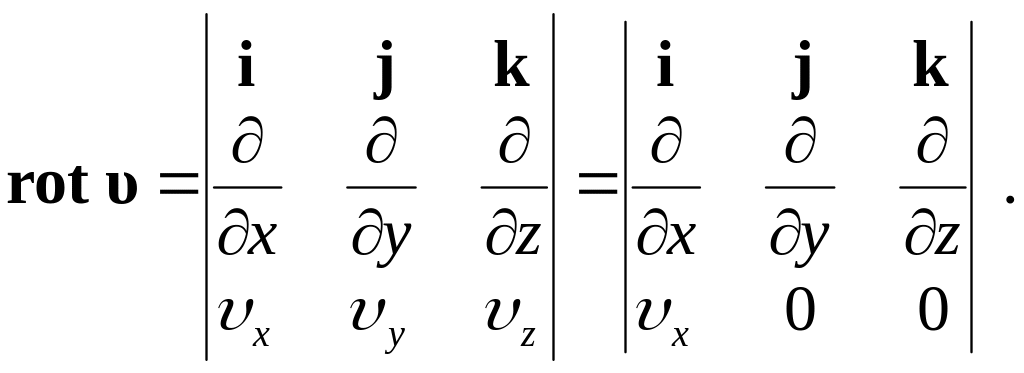- •Содержание
- •7. Идеальная среда
- •7.1. Уравнения движения для сжимаемой и несжимаемой идеальной среды
- •7.1.1. Замкнутая система уравнений сохранения для идеальной среды
- •7.1.2. Движение несжимаемой среды
- •7.1.3. Изоэнтропическое движение
- •7.1.4. Граничные и начальные условия
- •7.2. Уравнение Бернулли
- •7.2.1. Потенциальное движение идеальной среды
- •7.2.2. Линии тока и траектории. Трубка тока
- •7.2.3. Скорость истечения идеальной несжимаемой жидкости из сосуда
- •7.2.4. Распределение давления в трубе переменного сечения
- •7.2.5. Кавитация
- •7.2.6. Трубка Пито
- •7.3. Влияние сжимаемости среды
- •7.4. Вихревое движение
- •7.4.1. Сохранение циркуляции скорости. Теорема Томсона
- •7.4.2. Вихревая трубка. Теорема Гельмгольца
- •7.4.3. Прямолинейная одиночная вихревая нить
- •7.4.4. Примеры вихревых движений
- •7.5. Потенциальное движение
- •7.5.1. Потенциал скорости. Граничные условия
- •7.5.2. Функция тока для плоского движения идеальной среды
- •7.5.3. Свойства функции тока
- •7.6. Некоторые методы решения газодинамических задач для идеальной жидкости
- •7.6.1. Метод конформных отображений
- •7.6.2. Обтекание плоской пластинки идеальной несжимаемой жидкостью
- •7.6.3. Обтекание цилиндра идеальной несжимаемой жидкостью
- •7.6.4. Распределение давления на поверхности цилиндра. Парадокс Даламбера
- •7.7. Суперпозиция потенциальных потоков
- •7.7.1. Обтекание бесконечного цилиндра с циркуляцией
- •7.7.2. Распределение давления. Подъемная сила
- •7.7.3. Эффект Магнуса
- •7.8. Графоаналитический метод
- •7.8.1. Постановка задачи и сущность метода
- •7.9. Движение бесконечного цилиндра в идеальной несжимаемой среде
- •7.9.1. Постановка задачи и методика решения
- •7.9.2. Распределение давления около движущегося цилиндра
- •7.9.3. Сила сопротивления движущегося шара. Присоединенная масса
- •7.10. Численные методы в механике сплошных идеальных сред
- •7.10.1. Введение
- •7.10.2. Краткая характеристика численных методов
- •7.10.2.1. Метод конечных разностей
- •7.10.2.2. Метод интегральных соотношений
- •7.10.2.3. Метод характеристик
- •7.10.2.4. Метод частиц в ячейках
- •7.10.2.5. Метод конечных элементов
- •7.10.2.6. Метод дискретных вихрей
- •7.10.2.7. Статистические методы
- •7.10.3. Основы численных методов
- •7.10.3.1. Задача интерполирования
- •7.10.3.2. Интерполяционный многочлен Лагранжа
- •7.10.3.3. Погрешность интерполирования
- •7.10.4. Вычисление интегралов
- •7.10.4.1. Квадратурные формулы Ньютона-Котеса
- •7.10.4.2. Формула трапеций
- •7.10.4.3. Формула Симпсона
- •7.10.5. Численное дифференцирование
- •7.11. Применение метода потоков в механике сплошных идеальных сред
- •7.11.1. Общие замечания
- •7.11.2. Описание метода потоков
- •7.11.3. Конечно – разностные схемы метода потоков
- •7.11.3.1. Постановка и решение задачи
- •7.11.3.2. Обтекание прямоугольного выступа эйлеровым газом
- •7.11.3.3. Этапы вычислительного цикла
- •7.11.4. Результаты расчета
- •Литература:
7.4.3. Прямолинейная одиночная вихревая нить
Прямолинейной вихревой нитью называют область пространства, в которой среда вращается относительно неограниченно длинной прямолинейной оси симметрии. Рассмотрим такую нить, ось которой перпендикулярна плоскости (рис.7.8). Интенсивностью прямолинейной вихревой нити называют предел следующего вида
![]() (7.4.11)
(7.4.11)
Наличие вихря приводит к появлению некоторого поля скоростей среды вокруг центра нити. Для неограниченно длинной прямолинейной нити поле скоростей, очевидно, будет обладать цилиндрической симметрией. Движение жидкости одинаково во всех плоскостях, перпендикулярных нити. В этих плоскостях частицы двигаются по окружностям, центром которых является след нити на плоскости. Такое движение среды называют плоским вихрем. Закон изменения скорости частиц в плоском вихре в зависимости от расстояния от нити можно получить, если воспользоваться определением циркуляции скорости (7.4.1) и теоремой Томсона:
![]() (7.4.12)
(7.4.12)
Из (7.4.12) видно, что движение в таком вихре имеет особенность в точке r = 0, где .
Рис.7.8 |
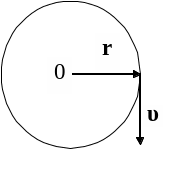
Рассмотрим один из примеров пло-ского
вихря с постоянной циркуляцией
(рис.7.8). Пусть индивидуальная частица
вращается в плоском вихре на расстоянии
r от центра вихря
со скоростью
|
![]() (7.4.13)
(7.4.13)
Если
частица в плоском вихре (см. рис.7.8)
вращается по часовой стрелке, то согласно
определению
направлен в сторону, откуда вращение
частицы наблюдается против движения
часовой стрелки, т.е.
направлен за плоскость чертежа (от
наблюдателя). Поэтому ненулевым является
только единственный орт направления
оси z, а именно
![]() ,
а
,
а
![]() .
Поэтому в (7.4.13) первое и второе слагаемое
равны 0. Поскольку для плоского вихря
составляющие скорости
.
Поэтому в (7.4.13) первое и второе слагаемое
равны 0. Поскольку для плоского вихря
составляющие скорости
![]() ,
а
,
а
![]() определяется в соответствии с (7.4.12), то
очевидно, что и третье слагаемое в
(7.4.13) также равно нулю, т.к.
определяется в соответствии с (7.4.12), то
очевидно, что и третье слагаемое в
(7.4.13) также равно нулю, т.к.
![]() .
.
Таким образом, в
плоском вихре (рис.7.8)
![]() = 0. Это означает, что движение среды в
таком плоском вихре является безвихревым,
т.е. потенциальным, и индивидуальные
частицы вращаются по окружности с
различными радиусами r
без вращения вокруг осей, проходящих
через них. Схематично такое движение
частиц изображено на рис.7.9. В природе
такое движение можно наблюдать при
истечении жидкости из сосуда с отверстием
в его дне, т.е. при наличии воронки на
поверхности жидкости.
= 0. Это означает, что движение среды в
таком плоском вихре является безвихревым,
т.е. потенциальным, и индивидуальные
частицы вращаются по окружности с
различными радиусами r
без вращения вокруг осей, проходящих
через них. Схематично такое движение
частиц изображено на рис.7.9. В природе
такое движение можно наблюдать при
истечении жидкости из сосуда с отверстием
в его дне, т.е. при наличии воронки на
поверхности жидкости.

Рис.7.9 Рис.7.10
Рассмотрим
теперь случай, когда жидкость вращается
как абсолютно твёрдое тело. Причем,
индивидуальная частица, находящаяся
на расстоянии
![]() от оси вихря (рис. 7.8), вращается с линейной
скоростью
от оси вихря (рис. 7.8), вращается с линейной
скоростью
![]() ,
где
есть угловая скорость вращения. Запишем
i - компоненту ротора
скорости движения индивидуальной
частицы, используя тензорную запись в
виде:
,
где
есть угловая скорость вращения. Запишем
i - компоненту ротора
скорости движения индивидуальной
частицы, используя тензорную запись в
виде:
![]()
Если в
первом символе Леви-Чивита дважды
переставить индекс
![]() ,
то его знак не изменится, т.е.
,
то его знак не изменится, т.е.
![]() .
Далее, запишем скалярное произведение
двух символов Леви-Чивита через разность
скалярных произведений соответствующих
символов Кронекера согласно шестого
свойства символа Леви-Чивита (см. п.
6.5) и проведем простейшие преобразования.
В результате имеем:
.
Далее, запишем скалярное произведение
двух символов Леви-Чивита через разность
скалярных произведений соответствующих
символов Кронекера согласно шестого
свойства символа Леви-Чивита (см. п.
6.5) и проведем простейшие преобразования.
В результате имеем:
![]() (7.4.14)
(7.4.14)
Следовательно,
i-я компонента ротора
линейной скорости движения индивидуальной
частицы
![]() в плоском вихре в среде, вращающейся
как абсолютно твёрдое тело, определяется
i-ой компонентой
угловой скорости мгновенного поворота
самой частицы. Поэтому при одном повороте
такой индивидуальной частицы в плоском
вихре вокруг некоторой оси она совершает
один оборот вокруг оси, проходящей
через неё (рис. 7.10). Таким образом,
движение среды в плоском вихре как
абсолютно твёрдого тела является
движением вихревым, не потенциальным
в плоском вихре в среде, вращающейся
как абсолютно твёрдое тело, определяется
i-ой компонентой
угловой скорости мгновенного поворота
самой частицы. Поэтому при одном повороте
такой индивидуальной частицы в плоском
вихре вокруг некоторой оси она совершает
один оборот вокруг оси, проходящей
через неё (рис. 7.10). Таким образом,
движение среды в плоском вихре как
абсолютно твёрдого тела является
движением вихревым, не потенциальным
![]() .
.
Рассмотрим ещё один
случай, когда частицы двигаются
прямолинейно вдоль некоторой плоской
поверхности в направлении оси х с
градиентом скорости по нормали к
поверхности (ось у). Пусть профиль
скорости определяется линейным законом
![]() (рис. 7.11). Запишем ротор скорости в виде
матрицы:
(рис. 7.11). Запишем ротор скорости в виде
матрицы:
Рис 7.11 |
Отличной
от нуля является только z-компонента
ротора
|
Таким образом, стационарное движение идеальной среды вдоль поверхности с некоторым профилем скорости является вихревым, поскольку с течением времени индивидуальная частица за счёт разности скоростей верхней и нижней её границ изменяет свою форму, вращаясь относительно проходящей через неё оси.
Не следует отождествлять
вихревое движение
![]() только с движением частиц по окружности:
не всякое движение по окружности
является вихревым и не всякое вихревое
движение есть движение по окружности.
Движение называют безвихревым
(потенциальным с
только с движением частиц по окружности:
не всякое движение по окружности
является вихревым и не всякое вихревое
движение есть движение по окружности.
Движение называют безвихревым
(потенциальным с
![]() )
только тогда, когда индивидуальные
частицы двигаются без вращения
относительно некоторых осей, проходящих
через сами частицы. В противном случае
движение называют вихревым, не
потенциальным с
)
только тогда, когда индивидуальные
частицы двигаются без вращения
относительно некоторых осей, проходящих
через сами частицы. В противном случае
движение называют вихревым, не
потенциальным с
![]() .
.