Вопрос 2. Регулярные методы оптимизации: динамическое программирование. Принцип оптимальности Беллмана и рекуррентное соотношение. Примеры задач управления запасами.

Метод динамического программирования

Данный метод, разработанный Р. Беллманом, позволяет решать вариационные задачи при сложном виде возможных управлений. Он получил широкое применение при решении транспортных задач, задач распределения ресурсов, замены оборудования и т.д. При проектировании метод динамического программирования может быть использован для оптимизации конфигураций деталей, если их поверхность представлена как некоторая траектория в пространстве.

Метод динамического программирования отвечает тому естественному ходу человеческой мысли, который был вырабо­тан эволюцией. Подобные методы оптимизации, основанные на идее последовательного анализа вариантов, в большой степени используют природу изучаемых задач.

В основе метода лежит сформулированный Р. Беллманом принцип оптимальности. Этот принцип верен для тех систем, последующее движение которых полностью определяется их

состоянием в текущий момент времени. К таким системам отно­сятся, например, управляемые системы, т.е. системы, аналогич­ные тем, для которых вводится принцип максимума.

Принцип оптимальности отражает важнейшие особенности задач оптимального управления. Его суть можно объяснять по-разному. Ввиду его важности приведем несколько формулировок.

Первая формулировка. Если управление оптимально, то, каковы бы ни были первоначальное состояние системы и управление системой в начальный момент времени, последующее управление оптимально относительно состояния, которое сис­тема примет в результате начального управления.

Указанное свойство - одно из основных, для процессов марковского типа, т.е. процессов, будущее поведение которых полно­стью определяется состоянием и управлением в настоящее время.

Вторая формулировка. Оптимальное управление в любой момент времени не зависит от предыстории системы и опреде­ляется только состоянием системы в этот момент и целью управления.

Е ще один вариант принципа оптимальности дадим для за-дачи оптимального управления с фиксированным временем и свободным правым концом. Пусть закон движения описывает­ся автономной системой дифференциальных уравнений (6.25), причем заданы начальный t₁ и конечный t₂ моменты времени, а также начальное состояние x(t₁) = х¹ . Целевой функционал оп­ределим следующим образом:

Третья формулировка. Начиная с любого момента време­ни t^'ϵ[t₁,t₂] участок оптимальной траектории также является оптимальной траекторией.

Другими словами, каково бы ни было положение точки x^*(t') на оптимальной фазовой траектории, ее участок от точки х*( t')участок 2 на рис. 6.10) тоже является оптимальной траекторией.

Что же касается участка 1 оптимальной траектории до точки x^*(t'), то можно утверждать, что этот участок есть оптимальная траектория, когда точка x*(t^') - х' является фиксированной, т.е. ко­гда по условию задачи допустимая траектория обязательно должна проходить через точку х'. Если же задана только начальная точка x*(t₁) - x¹, то участок 1 оптималь­ной траектории сам по себе может и не быть оптимальной траекто­рией, т.е. может не доставлять минимум целевому функционалу в задаче со свободным пра­вым концом.

Т аким образом, важно иметь в виду, что принцип опти­мальности относится к последующему за данным состоянием движению системы, но может нарушаться для движения, пред­шествующего данному состоянию. Следовательно, нужно под­черкнуть, что принцип оптимальности не может быть распро­странен на любой участок траектории движения.

О тметим еще одну особенность оптимального управле­ния, вытекающую из принципа оптимальности: выбор опти­мального управления определяется лишь состоянием системы в текущий момент времени Если в какой-то период времени управление было не оптимальным, то последствия этого в бу­дущем исправить уже нельзя

Билет №15

1. Регулярные методы оптимизации: линейное программирование. Виды исследуемых функций, общая постановка и примеры задач.

ЛП- неточный перевод – пл-е на осн-е линейных соотн-ий.

F(x)=c¹x¹+c²x²+…+cⁿxⁿ=(сбч)ю «nf a-z не ограничена, поэтому искать ее мах, не налагая ограничений на обл-ь изм-я вектора х, бессмысленно.. стесним вектор х многогранникомиз линейных равенств и неравенств. Тогда нужно найти величины х¹, хⁿ, доставляющие экстремум ф-ии.

Задача о выборе оптимального плана (выпуск с макс эф-ностью или мин затратами). Транспортная задача (наиб экономичный маршрут перевозки Т от складов к магазинам с учетом кол-ва). Отл-ся двойной индексацией переменных

2. Основы теории надёжности: определение вероятности безотказной работы, свойства функции вероятности безотказной работы и её графическое представление.

ВБР – в-ть того, что в пределах заданной наработки отказ объекта не возникнет. Если Т – время непрерывной исправно А; t – время, за кот необх опр-ть ВБР, то ВБР: P(t)= P{T>=t},t>=0. Св-ва ФВБР: 1) 0<=P(t)<=1; 2) ф-я P(t) – невозрастающая ф-я своего аргумента, т.е. если t₂>t₁, то P(t₂)<=P(t₁); 3) P(0)=1, P(∞)=0. Из 3):в-ть безотказной А опр-ся в предположении, что в нач момент т-и исчисления наработки об-т был работоспособен. + фото 7 (с 122-123 б)

Билет 16. Вопрос 1. Регулярные методы оптимизации: симплекс-метод решения задач линейного программирования.

Для линейных моделей может быть предложен детермини­рованный метод перебора возможных решений, позволяющий за конечное число итераций найти точное оптимальное решение. По существу, при этом происходит последовательное исследова­ние вершин некоторого полиэдрального множества, в связи с чем этот метод известен под названием симплекс-метода [10,24].

Предварительный анализ задачи линейного программиро­вания показывает, что для поиска оптимального решения необ­ходимо включить ограничения в функцию цели, а затем найти оптимальные значения переменных.

В общем случае эта задача не является тривиальной. Сим­плекс-метод предусматривает построение некоторого возможн ого базисного решения (предполагается, что множество допустимых решений не пусто и, значит, какие-то решения возможны) и его последовательное улучшение. Изложение метода це­лесообразно начать с рассмотрения простого примера.

Рассмотрим задачу линейного программирования: найти минимум функции

Формально изложенный метод сводится к выполнению следующих этапов.

1. В соответствии с числом ограничений вводятся дополнительные свободные переменные и задается первоначальное базисное решение, включающее в себя нулевые действительные переменные и ненулевые свободные переменные.

2. Проверяется возможность улучшения плана (симплекс-критерий I). Если улучшение возможно, осуществляется переход I процедуре 3. Если улучшение невозможно, решение считается окончательным (оптимальным) и вычисления прекращаются.

З. В соответствии с симплекс-критерием II выбирается путь улучшения плана, т.е. новая базисная переменная, и опре­деляется ее максимально допустимое значение. Одновременно определяется переменная, которую нужно исключить из базиса.

4. Изменяется базисное решение. Преобразуется систе­ма уравнений задачи, после чего осуществляется переход к процедуре 2.

Как уже отмечалось, задачи линейного программирования могут иметь множество равнозначных оптимальных решении. Симплекс-метод гарантирует получение одного из этих решений. Сама процедура симплекс-метода неоднозначна. Опреде­ленный произвол заключен как в выборе первоначального ба­зисного решения, так и пути совершенствования этого решения. В частности, в рассмотренном примере при первоначаль­ном улучшении по переменной х будет получено равнозначное (6.88) оптимальное решение (точка IV на рис. 6.12). I

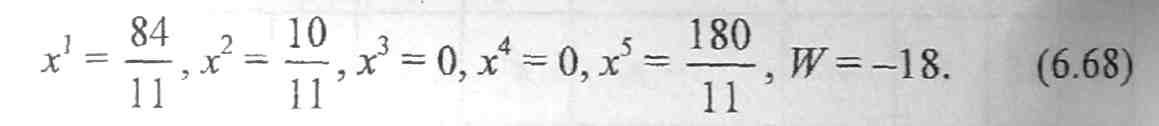
В тех случаях, когда линейная модель имеет более одного оптимального решения, она имеет бесконечное число таких ре­шений. При этом можно показать, что любое положительно взвешенное среднее двух оптимальных решений тоже является эквивалентным оптимальным решением. Для рассмотренного примера будут оптимальны все значения х¹ и х², отвечающие

Тот факт, что конечное оптимальное решение задачи линейного программирования, полученное с помощью симплекс-метода, всегда должно быть ассоциировано с допустимым ба­зисным решением, является тонкой особенностью симплекс -метода. Бели задача имеет одно ограничение, то независимо от числа видов производственной деятельности (переменных), включенных в модель, заранее известно, что в оптимальном ре­шении положительное значение может иметь только одна из этих переменных. Если добавляется еще одно ограничение, не являющееся избыточным, то положительное значение могут

????????????????????????????????????????????????????????? стр 269