Вопрос 2. Теория принятия решений: общие положения и область применения. Ситуация выбора решения. Факторы выбора альтернатив и этапы процесса принятия решений.

Т ЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ 5.2.1. Основные положения

Т еория принятия решений рассматривает задачи, где существует необходимость принимать решения в ситуациях, для которых не удается полностью учесть определяющие их усло­вия, а также последующее их влияние.

Теория принятия решений представляет собой набор по­нятий и систематических методов, позволяющих всесторонне анализировать проблемы принятия решений в условиях неопределенности.

Под ситуацией выбора решения следует понимать все элементы задачи, такие, как состояния исходных данных, варианты решения и их последствия, а также все оказывающие су­щественное влияние на решение внешние факторы как объективного, так и субъективного характера.

В основе теории принятия решений лежит предположение о том, что выбор альтернатив должен определяться двумя факторами: 1) представлениями лица, принимающего решение о веро­ятностях различных возможных исходов (последствий), которые могут иметь место при выборе того или иного варианта решения; 2) предпочтениями, отдаваемыми им различным возмож­ным исходам.

Варианты решения определяются, главным образом, па­раметрами системы или процесса. Факторы, влияющие на при­нятие решения, находятся в диапазоне от крайне субъективных, определяемых компетенцией и осведомленностью принимаю­щего решение и проявляющихся в ускоренном выборе или затя­гивании решения, до таких объективных условий, как техниче­ские данные, характеристики, методы и всевозможные вспомо­гательные средства. По затраченным для обработки средствам решения можно разбить на три группы: 1) эмпирические; 2) опирающиеся на некоторые количественные сравнительные оценки; 3) принятые на основании построенной с исчерпываю­щей полнотой модели.

Для удобства изложения выделим четыре важных этапа процесса принятия решений.

1. Определение альтернативных способов действия. Дол­жен быть задан подходящий набор целей и указаны соответст­вующие им меры эффективности;

2. Описание вероятностей возможных исходов. При этом требуется, чтобы неопределенность, связанная с альтернативными решениями, была выражена численно через распределе­ние вероятностей. В результате такой операции становится из­вестной вероятность каждого возможного исхода для каждого принятого решения,

3. Ранжирование предпочтений возможных исходов через их полезность. Для этого выбирают меру эффективности, а затем с ее помощью представляют в числовой форме отношение лица, принимающего решение, к возможным последствиям ре­шения и вероятности возможных исходов.

4. Рациональный синтез информации, полученной на первых трех этапах. Следует проанализировать и эффективно использо­вать всю полученную информацию для того, чтобы решить, какой из возможных альтернатив следует отдать предпочтение.

?????????????????????????????????????????????

Билет №12

1. Минимаксный критерий принятия решений: характеристика проектной ситуации и правило выбора варианта решения. Фото 7 (с 209 б)

Ищем в-т с макс знач-ем рез-та (мах е_i), считаем, что оц-и е_i хар-т такие вел-ны, как выигрыш.Выбор оптим в-та производим с пом критерия : Мн-во Е₀ оптимальных в-тов сост из тех Е_i0 , кот принадлежат мн-ву Е всех в-тов и оц-а е_i0 кот-х максимальна среди всех оц-к е_i.

2. Взаимосвязь между основными единичными показателями надёжности: вероятностью безотказной работы, средней наработкой на отказ и интенсивностью отказов (-характеристикой).

ВБР – в-ть того, что в пределах заданной наработки отказ объекта не возникнет. Если Т – время непрерывной исправно А; t – время, за кот необх опр-ть ВБР, то ВБР: P(t)= P{T>=t},t>=0

СНО – отн-е наработки восстанавливаемого об-а к математическому ожиданию числа его отказов в течение этой наработки.

ИО – отн-е числа отказов об-ов в ед-у т-и к среднему числу об-ов, продолжающих исправно работать в данный инт-л т-и.

Все они хар-т надежность невосстанавливаемых об-ов. (для восстанавливаемых наработка рассм-ся только до 1-го отказа) (с 122-130 б)

Билет 14. вопрос 1. Методы многомерной оптимизации: покоординатного спуска и градиентный.

2. Методы покоординатного спуска (метод Гаусса-Зейделя) (иногда их называют релаксационными методами). Эти методы преду­сматривают последовательную циклическую оптимизацию по каждой из варьируемых переменных х₁.

Направление движения к экстремуму выбирается пооче­редно вдоль каждой из координатных осей управляемых пара­метров х₁

Р ассмотрим процесс поиска экстремума целевой функции W(X) для n-мерной задачи оптимизации при X = (х₁, х₂,…х_n). Предположим, что осуществляется поиск минимума функции W(х). Тогда улучшению ее на шаге (k + 1) поиска будет соответствовать условие

И з выбранной начальной точки поиска Х₀ выполняется пробный шаг h₀ в положительном направлении одной из координатных осей (обычно вдоль оси первого управляемого пара­метра х₁). В новой точке Х₁ с координатами Х₁ = (x_1,1=x_1,0+h0,x_2,1=x_2,0,…x_n,0=x_n,0) вычисляется значение целевой функции W(Х) и сравнивается с ее значением в начальной точке W(X₀). Если W(X₁) < W(X₀) это направление принимается для осущест­вления дальнейшего пошагового движения к экстремуму в соот­ветствии с выражением

В противном случае производится, возврат в исходную точку Х₀ и движение осуществляется в отрицательном направ­лении оси х₁:

Движение в выбранном направлении оси х₁ выполняется до тех пор, пока целевая функция улучшается, т.е. выполняется условие (6.97). При его нарушении на шаге (k + 1) производится возврат в точку x_1,k, определяется направление движения вдоль следующей координатной оси x₂ и совершаются спуски в направлении, обеспечивающем улучшение целевой функции.

П осле осуществления спусков вдоль всей п осей первый цикл спусков N= 1 завершается и начинается новый цикл N=2. Если на очередном цикле движение оказалось невозможным ни по одной из осей, тогда уменьшается шаг поиска:

Далее поиск экстремума продолжается с уменьшенным шагом. Условие окончания поиска -

При достижении условия (6.102) поиск прекращается, и полученная точка Х_k принимается в качестве искомой экстре­мальной точки X. Точка X_k при этом находится в некоторой ма­лой окрестности точки локального экстремума X^* , ограничивае­мой задаваемым минимальным значением шага поиска h_min.

Параметрами алгоритма покоординатного спуска являются h_o, h_min и γ. Алгоритм обеспечивает сходимость к решению X* за конечное число итераций, если функция W(X) имеет первую и вторую производные в окрестности экстремума.

П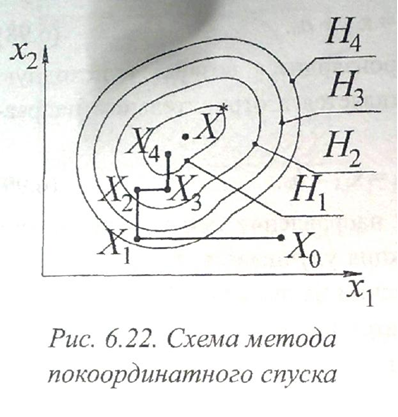 ример поиска экстре­мума методом покоординат­ного спуска для двумерной задачи при Х=(х₁,х₂) пред­ставлен на рис. 6.22, где пока­заны два цикла спусков вдоль осей х₁ и х₂ Линии равных уровней целевой функции W(X) обозначены Н₁ ..., Н₄, причем Н₁< Н₂< Н₃< Н₄, а минимум ее соответствует точке X*. Траектория поиска изображена жирной линией.

Движение начато из исходной точки X₀. При этом в каждом цикле вдоль каждой из осей выполняется несколько шагов. По­сле достижения точки Х₁ значение W(X) начинает возрастать, поэтому произошла смена направления движения. На новом на­правлении вдоль оси Х₂ движение осуществляется к точке Х₂ и первый цикл спусков на этом завершается. Затем циклы повто­ряются, пока не будет выполнено условие прекращения поиска.

3. Метод градиента

Г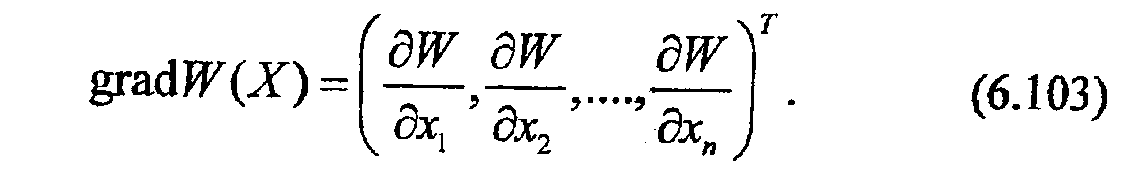 радиент - векторная величина, компонентами которой являются частные производные целевой функции по управляемым параметрам:

Градиент всегда сориентирован в направлении наиболее быстрого изменения функции. Градиентное направление является локально наилучшим направлением поиска при максимизации целевой функции, а антиградиентное - при ее минимизации. Это свойство вектора gradW(X) и используется в методе градиента, определяя вид траектории поиска.

Движение по вектору градиента перпендикулярно линиям уровня поверхности отклика (или перпендикулярно поверхности уровня в гиперпространстве в случае, если число проектных параметров больше двух).

Движение в пространстве управляемых параметров осу­ществляется в соответствии с выражением

где h_k - шаг поиска; S_к - единичный вектор направления поиска

н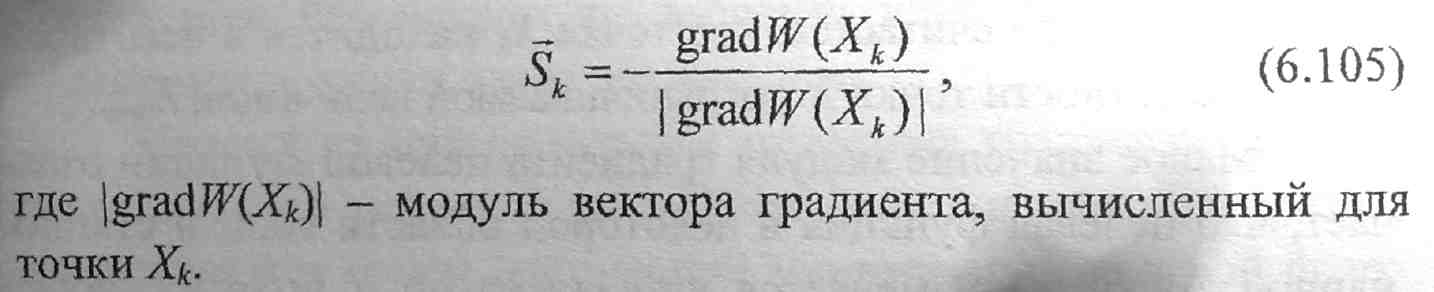 а шаге (k + 1), характеризующий направление градиента в точке Х_k,. При минимизации целевой функции вектор S_k должен иметь направление, противоположное направлению вектора гра­диента, поэтому для его определения используется выражение

Дадим краткое изложение алгоритма поиска минимума целевой функции W(X). В каждой точке траектории поиска Х_k, в том числе в исходной точке Х₀ определяется градиент целевой

функции gradW(X_k) и единичный вектор направления S_k вы­полняется шаг в пространстве управляемых параметров к точ­ке Х_к+1 согласно выражению (6.104) и оценивается успешность поиска на основе неравенства (6.97). При этом вычисляется зна­чение целевой функции W(X_k+1) в точке Х_к+1 и сравнивается с ее значением W(X_k+1) предыдущей точке Х_k.

Если условие (6.97) выполнено, то шаг поиска успешный, поэтому определяется новое направление движения из точки Х_k+1 и выполняется следующий шаг в точку Х_k+2

При большой кривизне линий равных уровней (т.е. при сложном рельефе поверхности целевой функции), а также вбли­зи экстремальной точки принятый в начале поиска шаг h_k может оказаться слишком большим, и условие (6.97) на очередном ша­ге не будет выполнено. В этом случае необходимо возвратиться в предыдущую точку h_k уменьшить шаг по формуле ™

где γ в коэффициент уменьшения шага: 0 <γ< 1, и повторить движение в том же направлении, но с меньшим шагом.

Условия окончания поиска методом градиента имеют вид

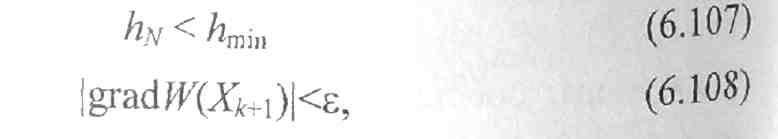
где ε - малая положительная величина.

При выполнении одного из условий: (6.107) или (6.107)-поиск прекращается, а полученная точка Х_k принимается в каче­стве искомой точки экстремума X. Если поиск прекращен по ус­ловию (6.107), то считается, что точка Х_k находится в некоторой малой окрестности точки X^*, ограничиваемой величиной h_min

Малое значение модуля градиента целевой функции озна­чает, что целевая функция в некоторой области вблизи стацио­нарной точки X* изменяется незначительно и поэтому любая точка в этой области может быть принята в качестве допустимо­го решения задачи оптимизации.

На рис. 6.23, а показан пример поиска минимума целевой функции для двумерной задачи методом градиента. Линии рав­ных уровней целевой функции обозначены H₁..., H₇, причем H₁<Н₂<...<Н₇ а траектория поиска проходит через точ­ки X₀, Х₁, Х₂… .

Д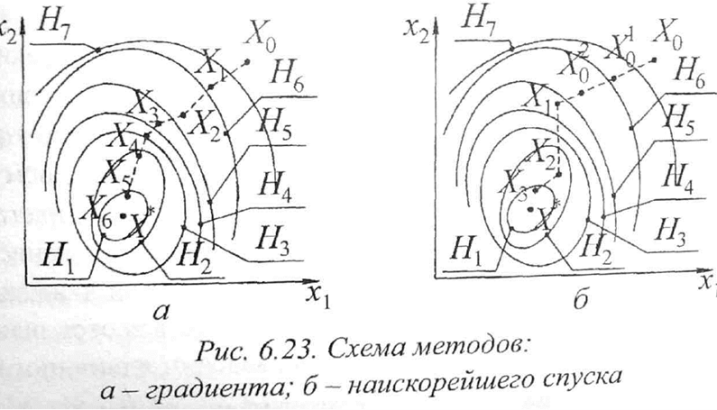 вижение в градиентном направлении по определению должно приводить к улучшению функции качества Если это не так и W(X_n+1) < W(X_n), можно предположить, что поиск просто «проскочил» оптимальную точку. В этом случае следует уменьшить величину шага и повторить вычисления.