Билет №7

1. Классификация математических моделей. Фото или обложка с методички

2. Методы оптимального проектирования. Критерии оптимальности технических объектов. Принцип Парето выделения области оптимальных значений управляемых параметров.

Для выбора наилучшего в-та из мн-ва необх сформулировать правило предпочтения. Основа правила - численная хар-ка об-а, кот отражает цель поиска, поэтому называется целевой ф-ей, или критерием оптиимальности. Задача оптимизации – поиск р, при кот целевая ф-я достигает экстремального знач-я. Поэтому те р, кот достигнут экстр. знач-я, считаются оптимальными. Если с повыш-ем кач-ва об-а цф возрастает, то оптим знач-я параметров соотв-т ее мах, иначе – мин. обычно задача оптимизации – многокритериальная задача. Общ принцип построения критериев оптимальности явл-ся оц-а эф-ти сист-ы с т зр ее полезности 4 сист-ы старшего ур-я. Поэтому в кач-ве критериев не д юз-ся внутр хар-ки сист-ы. Критерии мб стоимостные и технические. Ст отражают ст созд-я и ф-я сист-ы. Массовые критерии – тонно- или пассажирокилометр. (с 225 б)

Парето не выделяет единственного реш-я, а сужает мн-во альтернатив лет сбалансировать противоречия мд критериями и гет однозначное оптимально-компромиссное реш-е задачи выбора р программируемого об-а. (с 234-235 б)

Билет 8 вопрос 1. Регулярные методы оптимизации. Вариационное исчисление: задачи, приводящие к вариационному исчислению и уравнение Эйлера.

вариационное исчисление - это раздел математики посвященный нахождению наибольших и наименьших значений переменных величин, зависящих от выбора одной или нескольких функций.

Для дальнейшего изложения введем некоторые определе­ния. Функционалом называется переменная величина, зависящая от выбора одной или нескольких функций. В вариационном ис­числении важнейшими являются функционалы, заданные с по­мощью интегралов, например

П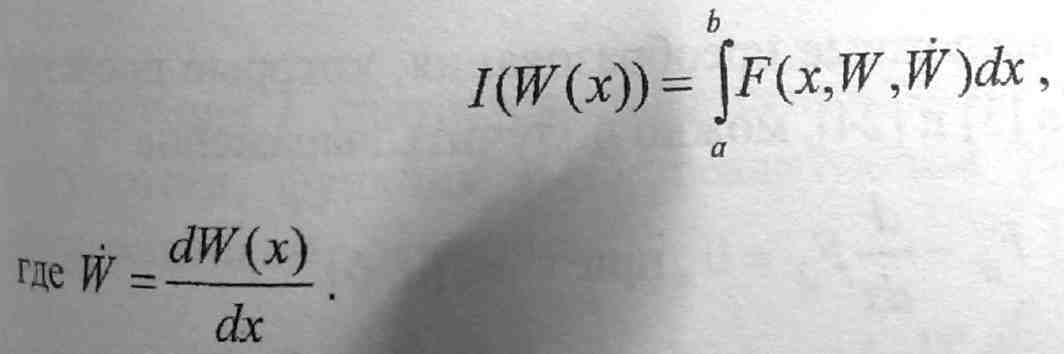 одынтегральная функция F(x,W,W) называется интегрантом функционала, предполагается непрерывной и имеющей непрерывные частные производные по всем переменным до второго порядка включительно.

К функционалам сводятся описания многочисленных баллистических и транспортных задач, задач, связанных с распреде­лением ресурсов и капиталовложений, с заменой оборудования и т.д.

Методы классического вариационного исчисления пригодны для оптимизации функционалов, определенных на классе гладких функций, у которых в рассматриваемой области непре­рывна первая производная, или на классе кусочно-гладких функций, у которых первая производная имеет конечное число разрывов первого рода. Основное соотношение вариационного исчисления - знаменитое уравнение Эйлера - выводится из ана­лиза изменений вариаций функционала I(W(x)), играющих роль производных функции W(x) [3].

Предполагается, что оптимальное (минимальное) значение функционала достигается на кривой W(x) (рис. 6.6), которая, таким образом, является оптимальной среди всех близких функ­ций W(x):

Выполнив несложные преобразования, которые представ лены, например, в [3] и [24], можно получить выражение

С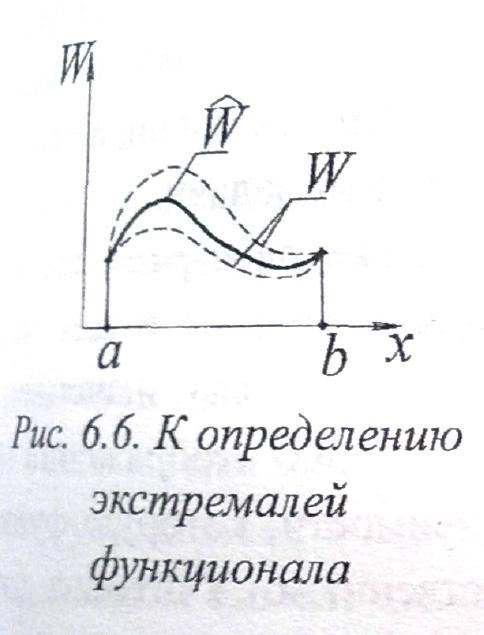 оотношение (6.20) и представляет собой уравнение Эйлера, выражающее необходимое условие экстремума и в той или иной форме лежащее в основе всех задач вариационного исчисления. Общее реше­ние уравнения Эйлера содержит две постоянные, для определения кото­рых, как правило, задаются значения функционала в начале и конце ис­следуемого интервала W(a), W(b).

Для уравнения Эйлера можно показать [3], что в случае мини­мума должны выполняться условия F_ww ≥ 0, а в случае макси­мума, наоборот, F_ww≤ 0.