2. Топологические уравнения

Для получения полной математической модели технической системы требуется объединение всех компонентных уравне­ний элементов в общую систему уравнений. Объединение осуще­ствляется на основе физических законов, выражающих условия равновесия и непрерывности фазовых переменных. Уравнения этих законов и называют топологическими уравнениями.

Топологические уравнения устанавливают связь между однородными фазовыми координатами, относящимися к различным элементам системы. Они получаются на основе сведе­ний о структуре системы и описывают характер взаимодействия между простыми элементами.

Условия равновесия записываются для фазовых переменных типа потенциала:

а условия непрерывности - для фазовых переменных типа потока

Если фазовые переменные - векторные величины, то направления векторов учитываются только топологическими уравнениями, а в компонентных уравнениях их направления не учитываются. Компонентные уравнения (2.6)-(2.8) в этом случае устанавливают соотношения лишь между модулями фазовых переменных. Это позволяет обеспечить корректное описание взаимодействия элементов системы в полной математической модели.

Вопрос 2. Элементы теории графов: основные понятия и определения.

Общие замечания, основные понятия и определения

Графы представляют собой наиболее абстрактную структуру, с которой приходится сталкиваться в курсах математической логики, дискретной математики, теории сетей связи. Любая система, предполагающая наличие дискретных состояний или узлов и переходов между ними, может быть описана графом.

Граф - это совокупность вершин (узлов) и связывающих их ребер (ветвей). Графы отображаются на плоскости набором точек и соединяющих их линий или векторов. При этом ветви могут отображаться и кривыми линиями, а их длина не играет никакой роли. Граф называется ориентированным (или орграфом), если некоторые ребра имеют определенное направление. Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Ребра орграфа называются дугами.

Смежные вершины графа - вершины, инцидентные одному и тому же ребру (принадлежащие одному ребру). Ребро графа определяется парой вершин. Два ребра, инцидентные одной и той же вершине (у которых есть общая вершина), также называются смежными (или соседними).

Математически граф G можно описать упорядоченной парой множеств N и A:

г де N - непустое множество, называемое множеством вершин; А -множество ребер, отражающее отношение между вершинами.

Часть графа - граф, образованный из исходного удалением некоторых вершин и ребер. Подграф - часть графа, образо­ванная некоторым подмножеством ребер и всеми инцидентными им вершинами. Суграф - часть графа, образованная удалением из исходного графа некоторых ребер.

Петлёй называется ребро, концевые точки которого совпадают. Степенью (валентностью) вершины называется число инцидентных ей ребер. Кратностью пары вершин называется число соединяющих их ребер.

Маршрут в графе - это последовательность смежных ре­бер (в этом случае ребра приобретают направление). Ясно, что можно определить маршрут и как последовательность смежных вершин. Маршрут называется циклом, если в нем первая вершина совпадает с последней.

Путь в графе - это маршрут без повторения вершин (а значит, и ребер). Т.е. путь - это последовательность дуг, в которой конечный узел каждой дуги является в то же время начальным узлом следующей дуги.

Цепь - маршрут, в котором все ребра различные. Замкнутая цепь является циклом. Т.е. цепь - это последовательность дуг, в которой каждая промежуточная дуга соединена с предше­ствующей концом или началом. Двигаясь вдоль цепи, можно пройти дугу в направлении, противоположном ее ориентации. Дуги, проходимые в направлении ориентации, называются пря­мыми дугами цепи, остальные - обратными дугами.

Контур - это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.

Граф является связным, если можно указать маршрут, охватывающий все вершины.

Сетью называется связный граф, в котором заданы «пропускные способности» ребер, т.е. числа с_ij. Это неотрицательные числа, причем с_ij = О тогда и только тогда, когда нет ребра, со­единяющего вершины i и j.

Д ерево графа - связный граф, не имеющий циклов.

Фундаментальное дерево (остов) — связный граф, не имеющий циклов.

Примеры графа, подграфа, суграфа и фундаментального дерева представлены на рис. 5.1.

В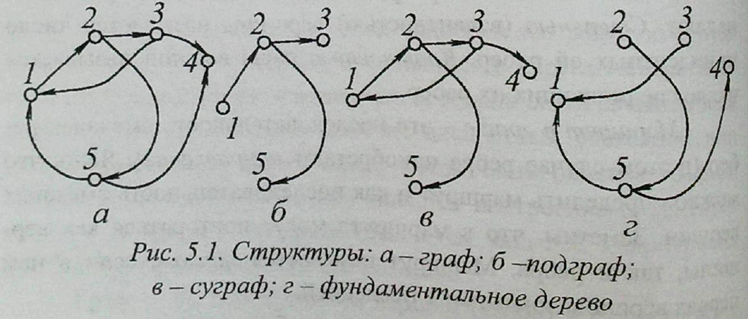 етви дерева - ребра графа, вошедшие в дерево. Хорды - ребра графа, не вошедшие в дерево.

Билет №4

1. Элементы теории надёжности технических объектов. Определение надёжности. Законы распределения случайных величин. Исправное сост-е, работоспособное сост-е, Непредельное неработоспособное сост-е, Предельное неработоспособное сост-е, Списание. Надежность - Св-во об-а сохранять во времени и в установленных пределах значение всех параметров, характеризующих его способность выполнять требуемые функции в заданных режимах и условиях применения, техобсл-я, ремонта, хр-я и тр-ки.Показатель н-ти – вероятностная вел-на, кол-ная хар-ка 1 или неск-х св-в, составл-х н-ть об-а. при расчетах пок-лей об-т мб рассмотен как эл-т или как сист-а. Эл-т – люб ус-во, сооруж-е, кар, аппарат, надежность кот-х изучают незав-мо от надежности составл-х его частей, те эл-т считают неделимым. (с. 11 с)Закон распредел-я – любое правило, позволяющее находить в-ть всевозм событий, связанных со СВ. напр, интегральный З распред-я: F,= в-ти того, чтослуч вел-на примет знач-е <x. Гр-к им ступенчатый вид. ( с. 116 б)

2. Дать определения понятиям “моделирование” и “модель”. Перечислить основные цели моделирования, преимущества математических моделей над другими формами моделирования. Модель – физ или абстрактн образ об-а, удобный для проведения иссл-ий и и дающий их адекватные рез-ты. Мме – ид эксперимент, кот лет оперативно оценить вл-е на раб пр-с люб ф-ра, в тч и такого, кот трудно поддается модел-ю. Мме лет гет сравнит-ные оц-и 4 кар, кот разл-ся по стр-ре, что редко достижимо при физ эксп-те.Юз 4 выбора рац параметров и схемs new кар, хар-к, выявл-ии предельных возм-тей и поиске путей модернизации. (с. 5 с). Мме лет до созд-я реальн сист-ы (об-а) рассм-ть возм-ные реж-ы А-ы, выбрать оптим управл возд-вия, составить объектин прогноз буд сост-ий сист-ы. Практическая ценность – лет рассчитать р не прибегая к реальн иссл-ям, кот дорогои и длит-ны.предв расчет, осн-ный на адеквтных ММ, лет избежать ош-к при проектировании узлов и ус-в, значит сильно сократить расходы ресурсов на созд-е и оп отработку образцов new техники. Пример с RP. (с 3 с)

Билет 5 вопрос 1. Моделирование надёжности технических объектов и систем: структурные и функциональные модели. Структурная схема надёжности объекта. Определение вероятности безотказной работы при последовательном, параллельном и смешанном соединении элементов?.

Общая характеристика и виды моделей

При определении показателей надежности объект может быть рассмотрен как элемент или как система.

Элемент — любое устройство, сооружение, машина, аппарат, надежность которых изучают независимо от надежности составляющих его частей, то есть элемент считают неделимым.

Под системой понимается совокупность элементов (или подсистем), объединенных конструктивно или функционально в соответствии с заданным алгоритмом взаимодействия при выполнении определенной задачи в процессе применения по назначению. Для системы известны показатели надежности составных частей (элементов) и установлено влияние отказа ка­ждого элемента на отказ системы.

В соответствии с представленной классификацией в теории надежности существуют два направления, Первое направление - системная, статистическая, или математическая, второе направление - физической теорией надежности.

В рамках этих направлений существуют два больших класса математических моделей надежности: структурные и функциональные.

В структурных моделях осуществляется определение значений показателей надежности объекта, обусловленное надежностью его элементов и разветвленностью связей между элементами. Они основаны на логических схемах взаимодействия элементов, входящих в систему, с точки зрения сохранения работоспособности системы в целом. Структурные модели представляют в виде схем и графов, а исходную информацию задают в виде известных значений вероятностей безотказной работы элементов, интенсивностей их отказов и т.п.

Расчет функциональной надежности - это определение показателей надежности выполнения объектом заданных функций. Функциональные модели учитывают механические, физические и другие реальные процессы,

Структурная схема надежности - это наглядное представление (графическое или в виде логических уравнений) условий, при которых работает или не работает исследуемый объект. Как правило, ССН объекта состоит из блоков, включающих различное число последовательно и параллельно включенных элементов.

Надежность непрерывной системы

П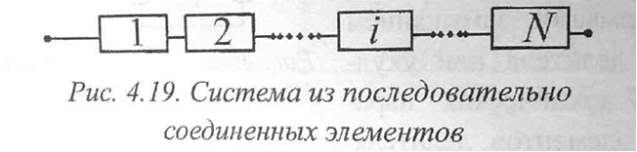 ростейшей ССН объекта является схема с последовательным соединением элементов (рис. 4.19). При этом полагают, что число элементов, образующих систему, конечно, а отказ од­ного элемента ведет к отказу системы.

При расчете показателей надежности такой системы обычно вводят довольно сильное допущение о том, что поток отказов является простейшим, т.е. функция плотности распределения отказов каждого элемента описывается экспоненциальным законом. При этом расчеты показателей надежности заметно упрощаются. Вероятность безотказной работы системы из N элементов в течении времени t определяется зависимостью:

г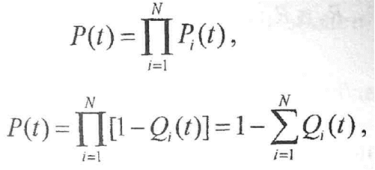 де Pi(f) - вероятность безотказной работы i-го элемента за время t; Qi - вероятность отказа i-го элемента системы.

Таким образом, формулы (4.105) и (4.106) соответствуют модели одновременной работоспособности всех элементов или отказа хотя бы одного элемента согласно правилам умножения и сложения вероятностей.

Представленный метод расчета надежности является наиболее простым и имеет свои недостатки. Во-первых, элементы в сис­теме работают в различных условиях эксплуатации. Во-вторых, на ранних стадиях проектирования (т.е. при ориентировочном расчете надежности) трудно установить режимы работы элементов. Поэтому данный метод в чистом виде целесообразно применять при окончательном расчете надежности, когда построены опытные образцы объекта и экспериментально определены режимы работы элементов.