Вопрос 2. Методы оптимального проектирования. Прямые методы многомерного поиска: классификация; сущность методов покоординатного спуска и градиентного.

Общая характеристика и классификация методов многомерной оптимизации

Реальные модели оптимального проектирования техниче­ских систем и их элементов почти всегда многомерны. Изучение многомерных задач сопряжено с рядом трудностей, не встре­чавшихся при одномерном поиске. Эти трудности резко нарас­тают с увеличением числа факторов и столь велики, что амери­канский математик и оптимизатор Р. Беллман назвал их «проклятием» размерности. Можно выделить три проблемы, порождаемые многомерностью.

Во-первых, возрастание числа переменных делает менее вероятной унимодальность поверхности отклика и часто приво­дит к необходимости изучения полимодальных функций.

Во-вторых, для многомерного случая не удается найти универсальную, не зависящую от удачи исследователя меру эф­фективности поиска, аналогичную принципу минимакса.

В-третьих, при переходе к многомерному пространству уменьшается относительная эффективность поиска, что связано с существенным увеличением интервала неопределенности по каждой из переменных при одинаковом относительном сокра­щении размеров области поиска. Это обстоятельство делает бесперспективными пассивные методы при решении многомер­ных задач.

Поэтому подавляющее большинство реально используе­мых методов многомерной оптимизации является последова­тельными, и далее будут рассматриваться только стратегии оп­тимизации указанного типа.

В настоящем разделе рассмотрены лишь некоторые наи­более типичные методы многомерного прямого поиска, разби­тые на группы в соответствии с классификацией, приведенной на рис. 6.19.

При разработке процедуры многомерного поиска всегдавозникает три вопроса:

1 Откуда (из какой точки х₀ ϵ X*) нужно начинать поиск?

2. В каком направлении необходимо двигаться в фактор­ном пространстве?

3. Когда необходимо прекратить поиск?

В зависимости от особенностей поверхности отклика и наличия ограничений в процессе поиска экстремума целевой функции применяют различные методы: безусловной и условной, ложной и глобальной оптимизации.

Б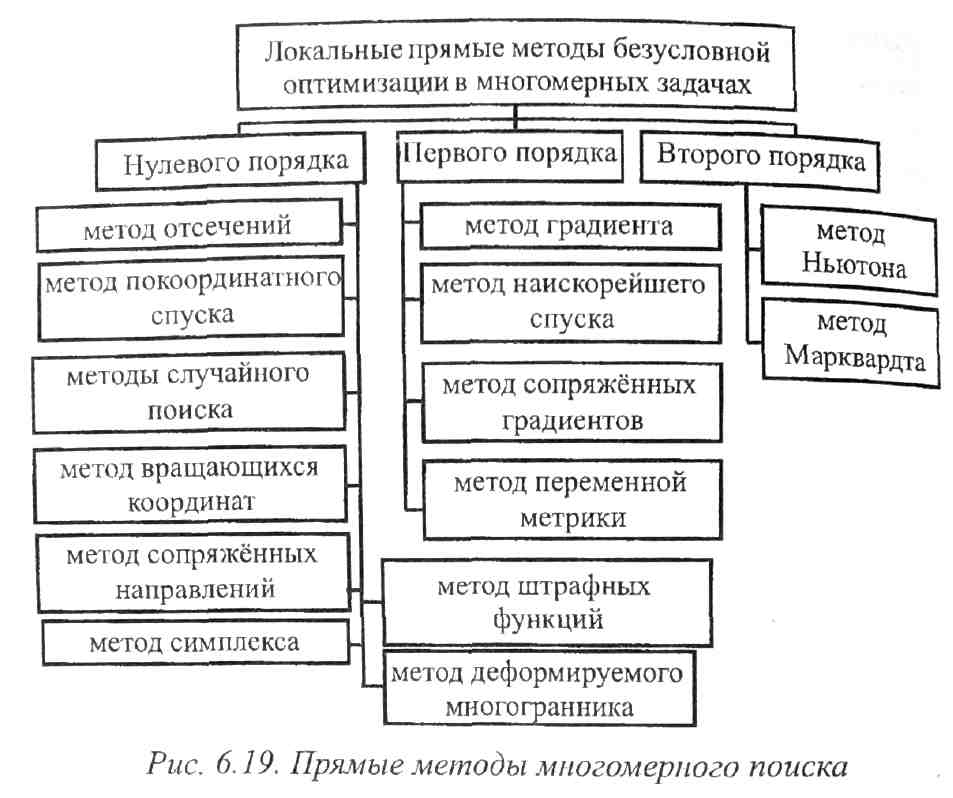 ольшинство методов оптимизаций разработано для по­иска безусловного экстремума. Но есть и методы, предназна­ченные для решения задач с ограничениями, которые различ­ными приемами сводят задачи условной оптимизации к задачам безусловной оптимизации.

Выбор начальной точки более или менее универсален для всех рассмотренных ниже методов оптимизации. Эта точка обычно задается в центре области X*. В ряде алгоритмов также используются случайные начальные точки.

При поиске экстремума движение в пространстве управ­ляемых параметров осуществляется шагами. От величины шага зависят многие параметры поиска.

Сущность метода оптимизации в первую очередь опреде­ляется способом выбора направления движения к экстремуму. В зависимости от порядка используемых при этом производных

целевой функции по управляемым параметрам различают мето­ды нулевого, первого и второго порядков.

В методах нулевого порядка информация о производных не используется. Методы первого порядка являются градиент­ными методами. В градиентных методах используются значения целевой функции и ее первых производных по управляемым параметрам. В методах второго порядка используются значения целевой функции, ее первых и вторых производных.

2. Методы покоординатного спуска (метод Гаусса-Зейделя) (иногда их называют релаксационными методами). Эти методы преду­сматривают последовательную циклическую оптимизацию по каждой из варьируемых переменных х₁.

Направление движения к экстремуму выбирается пооче­редно вдоль каждой из координатных осей управляемых пара­метров х₁

Рассмотрим процесс поиска экстремума целевой функции W(X) для n-мерной задачи оптимизации при X = (х₁, х₂,…х_n). Предположим, что осуществляется поиск минимума функции W(х). Тогда улучшению ее на шаге (k + 1) поиска будет соответствовать условие

И з выбранной начальной точки поиска Х₀ выполняется пробный шаг h₀ в положительном направлении одной из координатных осей (обычно вдоль оси первого управляемого пара­метра х₁). В новой точке Х₁ с координатами Х₁ = (x_1,1=x_1,0+h0,x_2,1=x_2,0,…x_n,0=x_n,0) вычисляется значение целевой функции W(Х) и сравнивается с ее значением в начальной точке W(X₀). Если W(X₁) < W(X₀) это направление принимается для осущест­вления дальнейшего пошагового движения к экстремуму в соот­ветствии с выражением

В противном случае производится, возврат в исходную точку Х₀ и движение осуществляется в отрицательном направ­лении оси х₁:

Движение в выбранном направлении оси х₁ выполняется до тех пор, пока целевая функция улучшается, т.е. выполняется условие (6.97). При его нарушении на шаге (k + 1) производится возврат в точку x_1,k, определяется направление движения вдоль следующей координатной оси x₂ и совершаются спуски в направлении, обеспечивающем улучшение целевой функции.

После осуществления спусков вдоль всей п осей первый цикл спусков N= 1 завершается и начинается новый цикл N=2. Если на очередном цикле движение оказалось невозможным ни по одной из осей, тогда уменьшается шаг поиска:

Далее поиск экстремума продолжается с уменьшенным шагом. Условие окончания поиска -

При достижении условия (6.102) поиск прекращается, и полученная точка Х_k принимается в качестве искомой экстре­мальной точки X. Точка X_k при этом находится в некоторой ма­лой окрестности точки локального экстремума X^* , ограничивае­мой задаваемым минимальным значением шага поиска h_min.

Параметрами алгоритма покоординатного спуска являются h_o, h_min и γ. Алгоритм обеспечивает сходимость к решению X* за конечное число итераций, если функция W(X) имеет первую и вторую производные в окрестности экстремума.

П ример поиска экстре­мума методом покоординат­ного спуска для двумерной задачи при Х=(х₁,х₂) пред­ставлен на рис. 6.22, где пока­заны два цикла спусков вдоль осей х₁ и х₂ Линии равных уровней целевой функции W(X) обозначены Н₁ ..., Н₄, причем Н₁< Н₂< Н₃< Н₄, а минимум ее соответствует точке X*. Траектория поиска изображена жирной линией.

Движение начато из исходной точки X₀. При этом в каждом цикле вдоль каждой из осей выполняется несколько шагов. По­сле достижения точки Х₁ значение W(X) начинает возрастать, поэтому произошла смена направления движения. На новом на­правлении вдоль оси Х₂ движение осуществляется к точке Х₂ и первый цикл спусков на этом завершается. Затем циклы повто­ряются, пока не будет выполнено условие прекращения поиска.

3. Метод градиента

Градиент - векторная величина, компонентами которой являются частные производные целевой функции по управляемым параметрам:

Градиент всегда сориентирован в направлении наиболее быстрого изменения функции. Градиентное направление является локально наилучшим направлением поиска при максимизации целевой функции, а антиградиентное - при ее минимизации. Это свойство вектора gradW(X) и используется в методе градиента, определяя вид траектории поиска.

Движение по вектору градиента перпендикулярно линиям уровня поверхности отклика (или перпендикулярно поверхности уровня в гиперпространстве в случае, если число проектных параметров больше двух).

Движение в пространстве управляемых параметров осу­ществляется в соответствии с выражением

где h_k - шаг поиска; S_к - единичный вектор направления поиска

на шаге (k + 1), характеризующий направление градиента в точке Х_k,. При минимизации целевой функции вектор S_k должен иметь направление, противоположное направлению вектора гра­диента, поэтому для его определения используется выражение

Дадим краткое изложение алгоритма поиска минимума целевой функции W(X). В каждой точке траектории поиска Х_k, в том числе в исходной точке Х₀ определяется градиент целевой

функции gradW(X_k) и единичный вектор направления S_k вы­полняется шаг в пространстве управляемых параметров к точ­ке Х_к+1 согласно выражению (6.104) и оценивается успешность поиска на основе неравенства (6.97). При этом вычисляется зна­чение целевой функции W(X_k+1) в точке Х_к+1 и сравнивается с ее значением W(X_k+1) предыдущей точке Х_k.

Если условие (6.97) выполнено, то шаг поиска успешный, поэтому определяется новое направление движения из точки Х_k+1 и выполняется следующий шаг в точку Х_k+2

При большой кривизне линий равных уровней (т.е. при сложном рельефе поверхности целевой функции), а также вбли­зи экстремальной точки принятый в начале поиска шаг h_k может оказаться слишком большим, и условие (6.97) на очередном ша­ге не будет выполнено. В этом случае необходимо возвратиться в предыдущую точку h_k уменьшить шаг по формуле ™

где γ в коэффициент уменьшения шага: 0 <γ< 1, и повторить движение в том же направлении, но с меньшим шагом.

Условия окончания поиска методом градиента имеют вид

где ε - малая положительная величина.

При выполнении одного из условий: (6.107) или (6.107)-поиск прекращается, а полученная точка Х_k принимается в каче­стве искомой точки экстремума X. Если поиск прекращен по ус­ловию (6.107), то считается, что точка Х_k находится в некоторой малой окрестности точки X^*, ограничиваемой величиной h_min

Малое значение модуля градиента целевой функции озна­чает, что целевая функция в некоторой области вблизи стацио­нарной точки X* изменяется незначительно и поэтому любая точка в этой области может быть принята в качестве допустимо­го решения задачи оптимизации.

На рис. 6.23, а показан пример поиска минимума целевой функции для двумерной задачи методом градиента. Линии рав­ных уровней целевой функции обозначены H₁..., H₇, причем H₁<Н₂<...<Н₇ а траектория поиска проходит через точ­ки X₀, Х₁, Х₂… .

Д вижение в градиентном направлении по определению должно приводить к улучшению функции качества Если это не так и W(X_n+1) < W(X_n), можно предположить, что поиск просто «проскочил» оптимальную точку. В этом случае следует уменьшить величину шага и повторить вычисления.

Билет 26. Вопрос 1. Элементы теории надёжности технических объектов. Определение надёжности и составляющие свойства надёжности: безотказность, долговечность, сохраняемость, ремонтопригодность. Законы распределения случайных величин.

4.1.1. Надежность объектов как комплексное свойство

В области математического моделирования теория надежности изучает задачи разработки вероятаостно-статиегических моделей, позволяющих прогнозировать время наступления и число отказов технических систем с целью выработки законо­мерностей, которых следует придерживаться при проектирова­нии, изготовлении, испытаниях и эксплуатации объектов для получения максимальной эффективности и безопасности их использования.

Надежность (в соответствии с ГОСТ 27.002-89) – это свойство объекта сохранять во времени в установленных преде­лах значения всех параметров характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки.

Надежность - это комплексный фактор, составляющими которого в общем случае являются свойства безотказности, дол­говечности, ремонтопригодности и сохраняемости, актуальность которых для конкретной системы определяется ее служебным назначением.

Б езотказность - это свойство объектов сохранять работо­способное состояние в течение некоторого времени или некоторой наработки. При оценке безотказности перерывы в работе объекта не учитываются. Безотказность характеризуется техническим со­стоянием объекта: исправностью, неисправностью, работоспо­собностью, неработоспособностью, повреждением и отказом.

И справное состояние - это такое состояние, при котором объект соответствует всем требованиям нормативно-технической и конструкторской документации. Неисправное состояние - это состояние, при котором объект не соответствует хотя бы одному из требований нормативно-технической и конструкторской доку­ментации. Событие, заключаю­щееся в нарушении работоспособного состояния объекта, назы­вается отказом. Событие, состоящее в нарушении исправного состояния объекта, но сохраняющего его работоспособность, но­сит название повреждения (дефекта).

Долговечность - это свойство объектов сохранять работо­способное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта. Предельное состояние объекта характеризуется тем, что даль­нейшее его применение по назначению недопустимо или неце­лесообразно.

Ремонтопригодность - это свойство объекта, заклю­чающееся в приспособленности к предупреждению и обнаружению причин отказов, повреждений и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонтов.

Сохраняемость - это свойство объекта сохранять значение показателей безотказности, долговечности и ремонтопригодности в течение и после хранения и (или) транспортирования.

Случайной величиной (СВ) называется переменная величи­на, значения которой зависят от случая, т.е. величина, способная принимать различные случайные значения.

Таким образом, закон распределения СВ - это любое правило (таблица, функция) позволяющее находить вероятности всевозможных событий, связанных со случайной величиной (например, вероятность того, что она примет такое-то значение или попадет на такой-то интервал).

2. Распределение непрерывных случайных величин Для непрерывной СВ понятие интегральной функции распределения имеет тот же смысл, что и для дискретной. Однако непрерывная величина X может принимать любые значения, находящиеся в некотором интервале [а; Ь], поэтому вероятность того, что она примет какое-либо определенное значение х, равна нулю, так как число возможных случаев бесконечно.