Вопрос 2. Прямые методы оптимизации: общая характеристика и примеры пассивных и последовательных стратегий поиска.

6.3.1. Общая характеристика методов и принцип минимакса

Область Х**, в которой лежит экстремум Х*, называется интервалом неопределенности. До проведения исследования интервал неопределенности совпадает с областью определения экстремума Х**=Х*. Лучшей будет та стратегия поиска, которая обеспечивает наибольшее сокращение интервала неопределен­ности (X**/Х* —► min) при фиксированных затратах на поиск или наименьшие затраты на поиск при заданном сокращении интервала неопределенности (наименьшее число исследованных точек факторного пространства п).

В зависимости от характера стратегии методы поиска принято делить на пассивные и последовательные. К пассивным относятся методы, при которых все точки факторного простран­ства для определения величины критерия задаются заранее до начала поиска. При этом дополнительная информация, получен­ная в процессе поиска, для выбора этих точек не используется.

Последовательные методы, наоборот, предусматривают выбор следующей точки факторного пространства на основе анализа результатов в уже исследованных точках. Последовательные методы приводят к более сложным алгоритмам, но обеспечива­ют более высокую эффективность поиска.

В зависимости от числа варьируемых переменных к мето­ды поиска делят на одномерные (к = 1) и многомерные (к ≥ 2).

Подавляющее большинство задач оптимального проекти­рования многомерно. Тем не менее методы одномерной оптими­зации представляют значительный интерес: во-первых, в неко­торых случаях при известной осторожности все-таки удается свести рассматриваемые задачи к одномерным; во-вторых, ме­тоды одномерной оптимизации являются составной частью большинства многомерных методов, и в-третьих, анализ одно­мерных методов позволяет наглядно продемонстрировать ос­новные идеи поиска вообще.

Билет 24. Вопрос 1. Электрическое аналоговое моделирование. Исследование моделей из сплошных проводящих сред и сетки сопротивлений для моделирования стационарных полей.

3.2.3. Модели стационарных полей

Существуют два способа построения электрических полей физических полей в элементах технических устройств. Модели могут быть построены из сплошных проводящих сред. В этом случае модельное поле характеризуется непрерывна распределением параметров, в частности, электрического потенциала. Можно построить также сеточные электрические модели, основанные на конечно-разностной аппроксимации непрерывного поля. В этом случае модельное поле задается дискретно в узлах сетки.

При использовании сплошных проводящих сред модель исследуемого объекта выполняется из сплошного проводящего материала. В качестве такого материала могут быть использова­ны любые среды, слабо проводящие электрический ток.

Для исследования полей в элементах конструкций машин могут быть созданы полноразмерные модели. Например, для изучения температурного поля в лопатке газовой турбины мож­но изготовить полноразмерную модель лопатки, задать на гра­ницах этой модели необходимые граничные условия, а затем измерить распределение потенциала в модели. Однако такие модели очень сложны и, главное, сугубо индивидуальны.

К счастью, большинство реальных полей обладает плоско­стной или осевой симметрией, позволяющей ограничиться изу­чением поля в одной характерной плоскости. Так, если пренеб­речь концевыми эффектами, можно считать, что распределение температур идентично в ряде последовательных сечений лопатки турбины. Точно так же идентичны в этих сечениях и поля скоростей обтекающего лопатку газа.

В подобных случаях достаточно изучить рассматриваемое поле или в тонком плоском (рис. 3.3, а), или в некотором клиновом слое (рис. 3.3, б), вырезанном плоскостями симметрии / и П. Возможность использования свойств симметрии и тонких слоев упрощает построение моделей, делает их универсальными. В электрическом поле плоскости симметрии могут быть выпол­нены из изолирующих материалов, на границе которых выпол­няется условие дφ/дп = 0.

П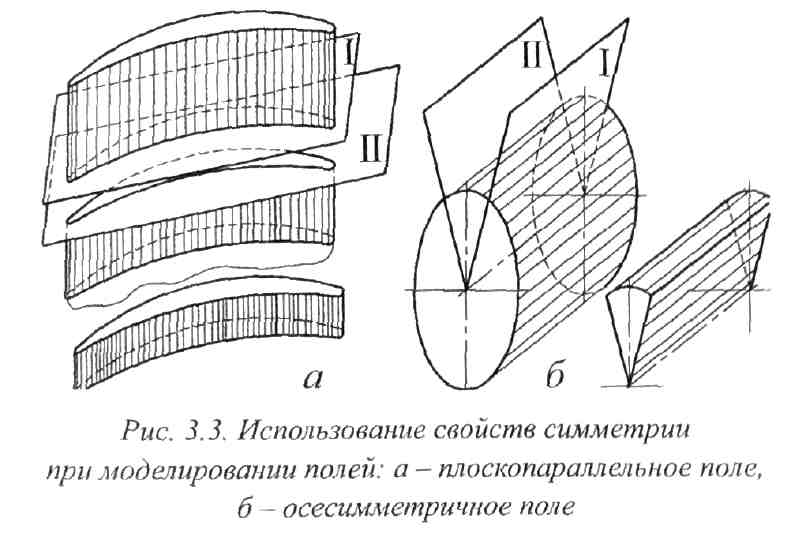 ри этом имитация клинового слоя требует увеличения проводимости проводящего слоя пропорционально радиусу мо­дели. Такой эффект можно получить или в плоском слое за счет соответствующего увеличения концентрации проводящего на­полнителя, или за счет изменения толщины проводящего слоя из однородного материала.

Для задания граничных условий при моделировании в сплошных проводящих средах используются электроды и изо­ляторы. Так, для задания на некотором участке границы модели

постоянного потенциала (ф|_г = const) необходимо установить, этом участке металлический электрод и подать на него соответствующее напряжение. В моделях из электропроводной бумаги такой электрод выполняется в виде металлической шины (рис. 3.4, а). В электролитической ванне металлический электрод устанавливается непосредственно на дно ванны (рис. 3.4, б)

Д ля задания некоторого распределения потенциала может быть использована ступенчатая аппроксимация этого распределения с помощью цепочки электродов (рис. 3.4, в) или установленая на границе специальная шина с заданным изменением потен­циала (рис. 3.4, г). Точно так же можно задать граничные усло­вия 2-го рода, только вместо потенциалов к границе должны быть подведены токи. Граничные условия 3-го рода могут быть заданы с помощью потенциалов, поданных к границам через заданные сопротивления (рис. 3.4, д).

Результаты моделирования представляются сеткой экви­потенциальных линий (ф = const), соответствующих изолиниям изучаемой функции. Получение такой сетки связано с решением двух задач: определением потенциала ф в заданных точках об­ласти и фиксацией найденных точек.

Использование сеточных моделей основано на конечно-разностной аппроксимации уравнений в частных производных.

Для электрического моделирования поля, описываемого уравнением Лапласа, может быть использована сетка рези­сторов R (R-сетка). Общий вид одного слоя сетки показан на рис. 3.5, а, схема узловой точки - на рис. 3.7, а. Согласно пер­вому закону Кирхгофа для каждой узловой точки сетки имеем:

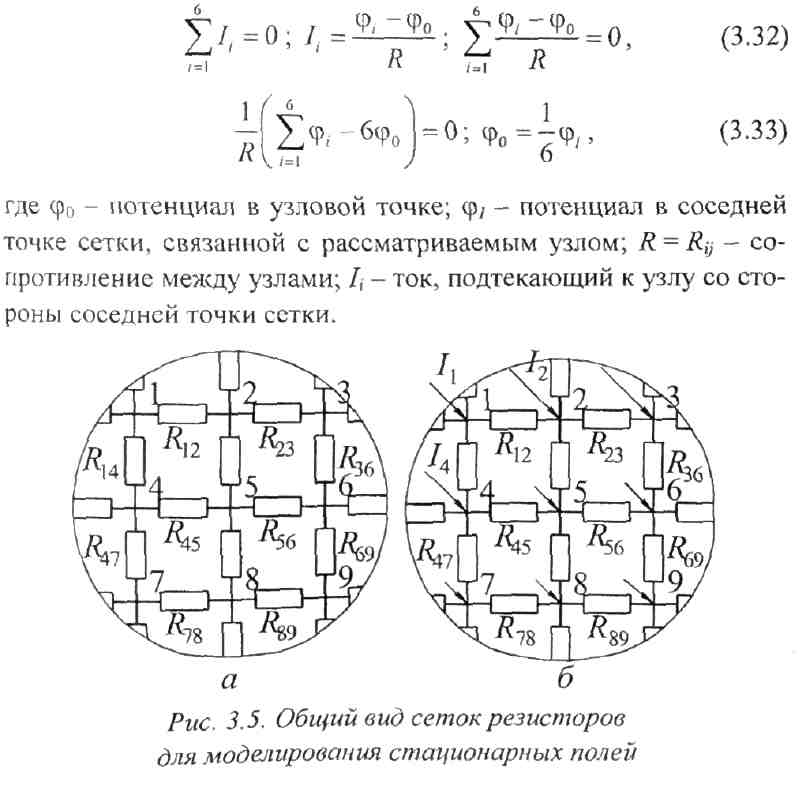
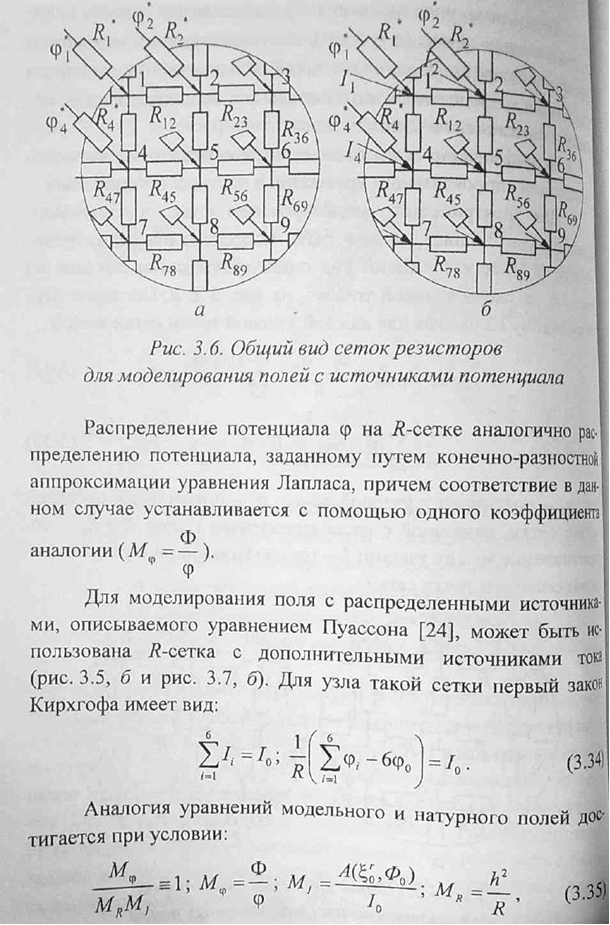
При создании конкретных моделей на основе сеток сопро­тивлений используются те же принципы, что и при использова­нии сплошных проводящих сред. Так, в силу симметрии моде­лирование плоскопараллельных и осесимметричных полей осу­ществляется на двумерной сетке сопротивлений, причем в по­следнем случае имитация клинового слоя достигается соответ­ствующим выбором сопротивлений (рис. 3.8).

Для изучения трехмерных полей могут быть использова­ны объемные сетки сопротивлений. Граничные условия задают­ся с помощью потенциалов, токов или потенциалов, подклю­ченных к конкретным граничным узлам сетки через заданные сопротивления. Задание постоянного потенциала осуществляет­ся закорачиванием граничных узлов. Разрыв цепей на границах

dφ = 0, и т.д.

дп

При использовании сеточных моделей реальные криволи­нейные границы области исследования заменяют их конечно-разностной аппроксимацией.

Сравнивая сеточные модели с моделями со сплошной проводящей средой, нужно учитывать следующие факторы. С одной стороны, использование конечно-разностной аппрок­симации всегда связано с внесением погрешности за счет пере­хода от производных к их конечно-разностным выражениям. Поэтому сеточные модели в принципе менее точны, чем модели из сплошной проводящей среды. С другой стороны, сеточные

модели существенно более удобны и универсальны. Они позво­ляют легко моделировать поля в неоднородных и анизотропных средах. Так, при моделировании поля температур в конструкци­ях, состоящих из материалов с различными теплопроводностями λ, достаточно просто изменить сопротивления между соот­ветствующими узловыми точками сетки.

Вопрос 2. Методы оптимального проектирования. Минимаксные стратегии поиска экстремума: методы Кифера и “золотого сечения”, их сравнительная характеристика с методом дихотомии и аналогия с динамическим программированием.

Метод золотого сечения.

Метод основан на делении текущего отрезка [а, b], где содержится искомый экстремум, на две неравные части, подчиняющиеся правилу золотого сечения, для определения следующего отрезка, содержащего максимум.

Золотое сечение определяется по правилу: отношение отрезка к большей его части равно отношению большей части отрезка к меньшей. Ему удовлетворяют две точки с и d, расположенные симметрично относительно середины отрезка.

Р ис. 3.3. Иллюстрация метода золотого сечения:

1 — интер­вал, включающий в себя иско­мый максимум функции после

первого этапа (первого золото­го сечения в точках c и d);

2 — то же, после второго этапа (но­вая точка е и старая точка d

Путем сравнения R(с) и R(d) определяют следующий отрезок, где содержится максимум. Если R(d) > R(с), то в качестве сле­дующего отрезка выбирается отрезок [с, b], в противном слу­чае — отрезок [a, d].

Поэтому на каждой следующей итерации (кроме "запуска" метода на исходном отрезке) нужно вычислять только одно зна­чение критерия оптимальности.

Новый отрезок снова делится на неравные части по правилу золотого сечения. Следует отметить, что точка d является и точ­кой золотого сечения отрезка [с, b], т.е.

Обозначим коэффициент золотого сечения k=db/cd, тогда можно получить квадратное уравнение для его нахождения

k=0,618

Решение уравнения применительно к первой итерации имеет вид

Условие окончания поис­ка — величина отрезка, содер­жащего максимум, меньше за­данной погрешности.

Метод обеспечивает более быструю сходимость к реше­нию, чем многие другие ме­тоды, и применим, очевидно, только для одноэкстремальных функций (в практических задачах под одноэкстремальной функцией понимают функцию, содержащую один экстремум того типа, который ищется в задаче).

На рис. 3.4 приведены два этапа поиска максимума функ­ции методом золотого сече­ния.

Дана функция

R(x)=sin(x+1),

Найти макси­мум на интервале: [-1,2]. Ошибка задается по х:  =0,05.

Результаты расчетов. Для "запуска" метода найдем две симметричные точки золотого сечения для отрезка [-1, 2]:

х₁ = 0,145898, х₂ = 0,85410197.

Значения критериев в этих точках соответственно R(x₁) = 0,911080, R(x₂) = 0,960136. Следовательно, новым отрезком является [0,145898,2], внутри которого находится максимальное из найденных значений R. Точка золотого сечения для нового отрезка будет х₃ = 0,58359214, a R(x₃) = 0,99991813. Далее приведены только координаты лучших точек при очередном шаге, номер шага и значения критерия в этих точках.

x₃ = 0,584 R₃ = 0,9999 x₄ = 0,584 R₄ = 0,9999

С точностью до четырёх значащих цифр задача решена на третьей итерации

d)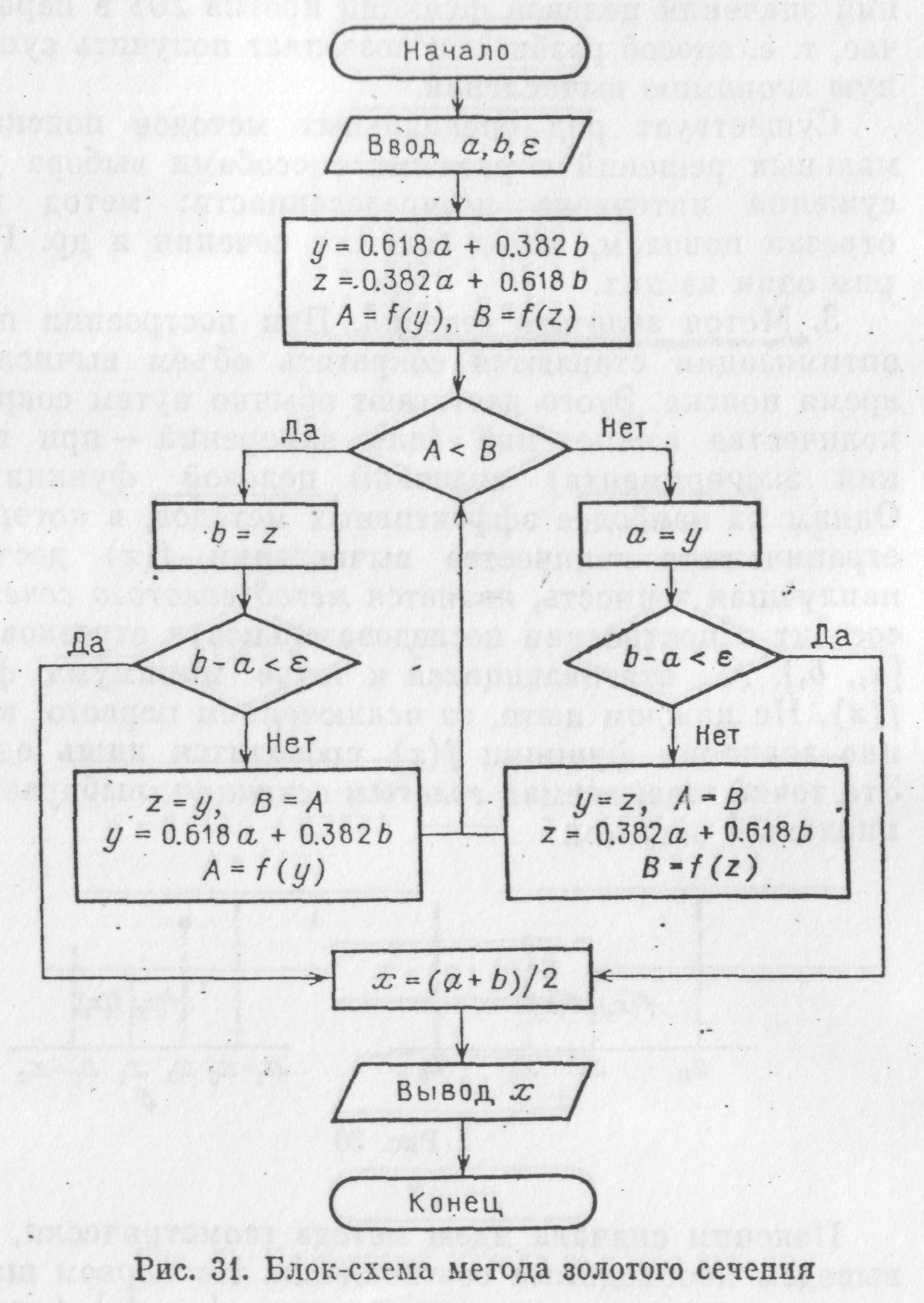

Рис. 3.5

Билет 25. Вопрос 1. Электрическое аналоговое моделирование. Исследование моделей из сплошных проводящих сред и сетки сопротивлений для моделирования стационарных полей.

3.2.3. Модели стационарных полей

Существуют два способа построения электрических полей физических полей в элементах технических устройств. Модели могут быть построены из сплошных проводящих сред. В этом случае модельное поле характеризуется непрерывна распределением параметров, в частности, электрического потенциала. Можно построить также сеточные электрические модели, основанные на конечно-разностной аппроксимации непрерывного поля. В этом случае модельное поле задается дискретно в узлах сетки.

При использовании сплошных проводящих сред модель исследуемого объекта выполняется из сплошного проводящего материала. В качестве такого материала могут быть использова­ны любые среды, слабо проводящие электрический ток.

Для исследования полей в элементах конструкций машин могут быть созданы полноразмерные модели. Например, для изучения температурного поля в лопатке газовой турбины мож­но изготовить полноразмерную модель лопатки, задать на гра­ницах этой модели необходимые граничные условия, а затем измерить распределение потенциала в модели. Однако такие модели очень сложны и, главное, сугубо индивидуальны.

К счастью, большинство реальных полей обладает плоско­стной или осевой симметрией, позволяющей ограничиться изу­чением поля в одной характерной плоскости. Так, если пренеб­речь концевыми эффектами, можно считать, что распределение температур идентично в ряде последовательных сечений лопатки турбины. Точно так же идентичны в этих сечениях и поля скоростей обтекающего лопатку газа.

В подобных случаях достаточно изучить рассматриваемое поле или в тонком плоском (рис. 3.3, а), или в некотором клиновом слое (рис. 3.3, б), вырезанном плоскостями симметрии / и П. Возможность использования свойств симметрии и тонких слоев упрощает построение моделей, делает их универсальными. В электрическом поле плоскости симметрии могут быть выпол­нены из изолирующих материалов, на границе которых выпол­няется условие дφ/дп = 0.

П ри этом имитация клинового слоя требует увеличения проводимости проводящего слоя пропорционально радиусу мо­дели. Такой эффект можно получить или в плоском слое за счет соответствующего увеличения концентрации проводящего на­полнителя, или за счет изменения толщины проводящего слоя из однородного материала.

Для задания граничных условий при моделировании в сплошных проводящих средах используются электроды и изо­ляторы. Так, для задания на некотором участке границы модели

постоянного потенциала (ф|_г = const) необходимо установить, этом участке металлический электрод и подать на него соответствующее напряжение. В моделях из электропроводной бумаги такой электрод выполняется в виде металлической шины (рис. 3.4, а). В электролитической ванне металлический электрод устанавливается непосредственно на дно ванны (рис. 3.4, б)

Д ля задания некоторого распределения потенциала может быть использована ступенчатая аппроксимация этого распределения с помощью цепочки электродов (рис. 3.4, в) или установленая на границе специальная шина с заданным изменением потен­циала (рис. 3.4, г). Точно так же можно задать граничные усло­вия 2-го рода, только вместо потенциалов к границе должны быть подведены токи. Граничные условия 3-го рода могут быть заданы с помощью потенциалов, поданных к границам через заданные сопротивления (рис. 3.4, д).

Результаты моделирования представляются сеткой экви­потенциальных линий (ф = const), соответствующих изолиниям изучаемой функции. Получение такой сетки связано с решением двух задач: определением потенциала ф в заданных точках об­ласти и фиксацией найденных точек.

Использование сеточных моделей основано на конечно-разностной аппроксимации уравнений в частных производных.

Для электрического моделирования поля, описываемого уравнением Лапласа, может быть использована сетка рези­сторов R (R-сетка). Общий вид одного слоя сетки показан на рис. 3.5, а, схема узловой точки - на рис. 3.7, а. Согласно пер­вому закону Кирхгофа для каждой узловой точки сетки имеем:

При создании конкретных моделей на основе сеток сопро­тивлений используются те же принципы, что и при использова­нии сплошных проводящих сред. Так, в силу симметрии моде­лирование плоскопараллельных и осесимметричных полей осу­ществляется на двумерной сетке сопротивлений, причем в по­следнем случае имитация клинового слоя достигается соответ­ствующим выбором сопротивлений (рис. 3.8).

Для изучения трехмерных полей могут быть использова­ны объемные сетки сопротивлений. Граничные условия задают­ся с помощью потенциалов, токов или потенциалов, подклю­ченных к конкретным граничным узлам сетки через заданные сопротивления. Задание постоянного потенциала осуществляет­ся закорачиванием граничных узлов. Разрыв цепей на границах

dφ = 0, и т.д.

дп

При использовании сеточных моделей реальные криволи­нейные границы области исследования заменяют их конечно-разностной аппроксимацией.

Сравнивая сеточные модели с моделями со сплошной проводящей средой, нужно учитывать следующие факторы. С одной стороны, использование конечно-разностной аппрок­симации всегда связано с внесением погрешности за счет пере­хода от производных к их конечно-разностным выражениям. Поэтому сеточные модели в принципе менее точны, чем модели из сплошной проводящей среды. С другой стороны, сеточные

модели существенно более удобны и универсальны. Они позво­ляют легко моделировать поля в неоднородных и анизотропных средах. Так, при моделировании поля температур в конструкци­ях, состоящих из материалов с различными теплопроводностями λ, достаточно просто изменить сопротивления между соот­ветствующими узловыми точками сетки.