Билет 1 вопрос 1. Виды моделей технических объектов. Определение математической модели и математического моделирования как метода проектирования технических объектов.

М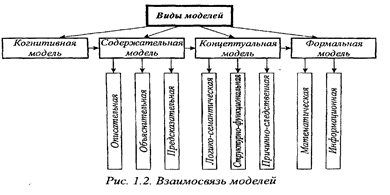 атематическое моделирование - это идеальное научное формальное моделирование, при котором описание объекта осуществляется на языке математики, а исследование модели проводится с использованием тех или иных математических методов.

Математическое моделирование позволяет посредством математических символов и зависимостей составить описание функционирования технического объекта в окружающей внешней среде, определить выходные параметры и характеристики, получить оценку показателей эффективности и качества, осуществить поиск оптимальной структуры и параметров объектов. Одним из основных компонентой системы проектирования в этом случае становится математическая модель (ММ).

Математическая модель - это совокупность математических объектов и отношений между ними, адекватно отображающая физические свойства технического объекта. В качестве математических объектов выступают числа, переменные, мно­жества, векторы, матрицы и т.п. Процесс же формирования ма­тематической модели и использования ее для анализа и синтеза при решении проектных задач называется математическим мо­делированием.

Математическое моделирование — это идеальный эксперимент позволяющий оперативно оценить влияние на рабочий процесс любого фактора, в том числе и такого, который трудно поддается натурному моделированию.

Вопрос 2. Критерий Сэвиджа принятия решений: характеристики проектной ситуации и выбор варианта.

3. Критерий Сэвиджа (S-критерий). Критерий Сэвиджа соответствует позиции относительного пессимизма (5.55). С помощью обозначений

Д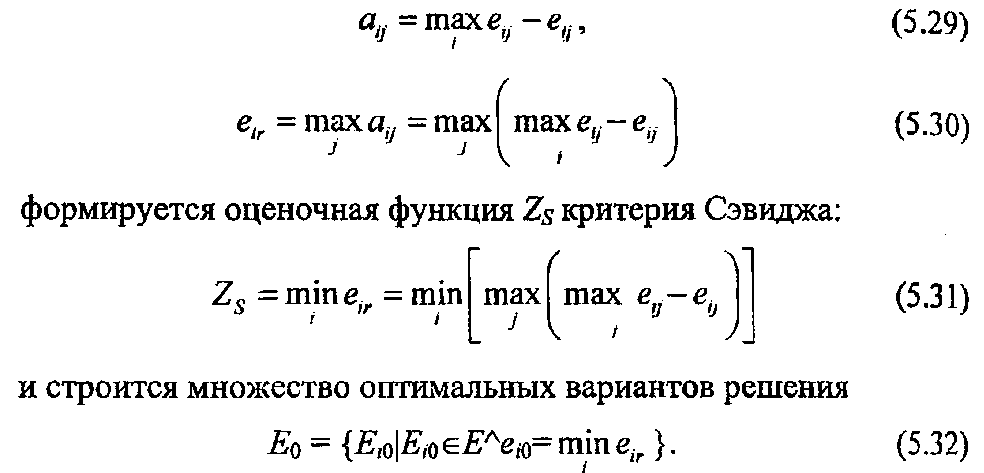 ля понимания этого критерия определяемую соотноше­нием величину a_ij=max e_ij-e_ij можно трактовать как максимальный дополнительный выигрыш, который достигается, ес­ли в состоянии F_j вместо варианта E_i выбрать другой, опти­мальный для этого внешнего состояния вариант. Мы можем, однако, интерпретировать a_ij как потери (штрафы), возни­кающие в состоянии F_i при замене оптимального для него ва­рианта на вариант E_i. Тогда определяемая соотношением вели­чина e_ir представляет собой - при интерпретации a_ij в качестве потерь - максимальные возможные (по всем внешним состояниям F_j, j= 1, 2,..., п) потери в случае выбора варианта E_i. Эти максимально возможные потери минимизируются за счет выбора подходящего варианта E_i

Соответствующее S-критерию правило выбора теперь ин­терпретируется так: каждый элемент матрицы решений ||е_ij|| вычитается из наибольшего результата max_i e_ij соответст­вующего столбца. Разности a_ij образуют матрицу остатков ||а_ij||. Эта матрица пополняется столбцом наибольших разно­стей e_ir. Выбираются те варианты Е_i0, в строках которых стоит наименьшее для этого столбца значение.

По выражению для S-критерия оценивается значение ре­зультатов тех состояний, которые, вследствие выбора соответст­вующего распределения вероятностей, оказывают одинаковое влияние на решение. С точки зрения результатов матрицы ||е_ij|| S-критерий связан с риском, однако с позиций матрицы ||е_ij|| он от риска свободен. В остальном к ситуации принятия решений предъявляются те же требования, что и в случае ММ-критерия.

Билет 2 вопрос 1. Последовательность процесса построения математической модели. Основное содержание этапов.

Построение любой математической модели можно ус­ловно представить состоящим из 7 этапов (рис. 1.3). Рассмотрим сущность этих этапов.

1 . Содержательная постановка задачи моделирования: перечень сформулированных в содержательной форме основных вопросов об объекте моделирования, интересующих исследователя. Это есть словесно-смысловое описание объекта или явления, которое содержит сведения об его природе и целях его исследования.

2. Концептуальная постановка задачи моделирования - это сформулированный в терминах конкретных дисциплин (физики, химии, биологии и т.д.) перечень основных вопросов, интересующих исследователя, и совокупность гипотез относительно свойств и поведения объекта моделирования.

3. Математическая постановка задачи моделирования - это совокупность математических соотношений, описывающих поведение и свойства объекта моделирования.

На этом этапе осуществляется выбор и формулировка закона (вариационного принципа, аналогии, закона сохранения и т.п.), которому подчиняется объект, и его запись в математической форме: выбирается (или строится) «эквивалент» объекта, отражающий в математической форме важнейшие его свойства.

4. Выбор и обоснование метода решения задачи. Выбор метода исследования в значительной степени зависит от квалификации и опыта членов рабочей группы. Аналитические методы более удобны для последующего анализа результатов, но применимы лишь для относительно простых моделей. В случае если математическая задача допускает аналитическое решение, последнее, без сомнения, предпочтительнее численного.

5. Реализация математической модели в виде программы для ЭВМ (численный эксперимент,

6. Проверка адекватности модели. Под адекватностью математической модели будет пониматься степень соответствия результатов, полученных по разработанной модели, данным эксперимента или тестовой задачи.

Проверка адекватности модели преследует две цели:

1) убедиться в справедливости совокупности гипотез, сформулированных на этапах концептуальной и математической постановок; 2) установить, что точность полученных результатов соответствует точности, оговоренной в техническом задании.

Проверка разработанной модели выполняется путем сравнения с экспериментальными данными о реальном объекте или с результатами других, созданных ранее и хорошо себя зарекомендовавших моделей. В первом случае говорят о проверке путем сравнения с экспериментом, во втором о сравнении с результатами решения тестовой задачи;

7. Практическое использование построенной модели и анализ результатов моделирования.

Данный этап включает оценку и обобщение результатов вычислений по следующим направлениям: -выявление закономерностей, которые позволяют оптимизировать или уточнить процесс;- уточнение области применения модели и оценка возможности ее упрощения с целью повышения эффективности при сохранении требуемой точности;- возможности дальнейшего развития модели; - проведение параметрических исследований с целью определения влияния отдельных характеристик системы или процесса на выходные параметры, которые определяются в результате моделирования.