Московский государственный технический университет имени Н.Э.Баумана.

Реферат на тему

«Разработка алгоритмов поддержки принятия решений с помощью выбора лучшей многокритериальной альтернативы на основе метода «ШНУР».

По курсу «Системный анализ и принятие решений»

Выполнила Студентка

группы

БМТ2-61

Головкина Наталия.

Преподаватель

Анищенко Леся Николаевна.

Москва,2013

План:

1. Введение

2. Отличия рассматриваемого метода от аналогов.

3. Формальная постановка задачи, исходные данные, необходимые для её решения, варианты её решения

4. Блок-схема алгоритма (алгоритмов), реализующих технологию принятия решений

5. Пример задачи из области биомедицинской инженерии, для решения которой следует использовать разработанный алгоритм

6. Список используемой литературы.

Введение.

В современной науке о принятии решений центральное место занимают многокритериальные задачи выбора. Для подавляющего большинства решений, принимаемых людьми, нельзя точно рассчитать и определить их последствия, а можно только предполагать, что определённый вариант решения приведёт к наилучшему результату. Проблемы принятия решения принято делить на структурированные, слабо структурированные и неструктурированные. В хорошо структурированных проблемах существенные зависимости между основными характеристиками могут быть выражены количественно. Неструктурированные проблемы характеризуются тем, что в их описании преобладают качественные факторы, трудно поддающиеся формализации, а количественные зависимости между этими факторами не определены. Слабоструктурированные проблемы занимают промежуточное положение, сочетая в себе количественные и качественные зависимости, причём недостаточно определённые стороны проблемы имеют тенденцию доминировать

Считается, что учет многих критериев приближает постановку задачи к реальной жизни. Традиционно принято различать три основные задачи принятия решений.

Первая из них – это упорядочение альтернатив. Для ряда задач представляется вполне обоснованным требование определить порядок на множестве альтернатив. Так, члены семьи упорядочивают по степени необходимости будущие покупки, руководители фирм упорядочивают по прибыльности объекты капиталовложений и т.д. В общем случае требование упорядочения альтернатив означает определение относительной ценности каждой из альтернатив.

Вторая - распределение альтернатив по классам решений. Такие задачи часто встречаются в повседневной жизни. Так, при покупке квартиры или дома, при обмене квартиры люди обычно делят альтернативы на две группы: заслуживающие и не заслуживающие более подробного изучения, требующего затрат сил и средств. Группы товаров различаются по качеству. Абитуриент делит на группы вузы, в которые он стремится поступить. Точно так же люди часто выделяют для себя группы книг (по привлекательности для чтения), туристские маршруты и т.д.

Третья - выделение лучшей альтернативы. Эта задача традиционно считалась одной из основных в принятии решений. Она часто встречается на практике. Выбор одного предмета при покупке, выбор места работы, выбор проекта сложного технического устройства — эти примеры хорошо знакомы. Кроме того, такие задачи распространены в мире политических решений, где альтернатив сравнительно немного, но они достаточно сложны для изучения и сравнения. Например, необходим лучший вариант организации обмена денег, лучший вариант проведения земельной реформы и т.д. Заметим, что особенностью многих задач принятия политических решений является конструирование новых альтернатив в процессе решения проблем.

Отличия рассматриваемого метода от аналогов.

Задачи ранжирования альтернатив (объектов, вариантов ре­шений, способов действий) по качеству и выбора лучшей из них являются близкими в том смысле, что последовательное выде­ление лучших альтернатив из заданного множества позволяет осуществить их ранжирование. Во многих случаях при выборе лучшей альтернативы ис­пользуется парное сравнение альтернатив и исключение худших в паре.

Цель метода выделения лучшей альтернативы должна со­стоять в помощи ЛПР при решении двух типов задач: задача выделения из многих многокритериальных аль­тернат и потенциально лучшей и задача сравнения двух альтернатив но многим критериям. От решения первой задачи ЛПР вообще можно освободить, пору­чив ее решение компьютеру, поскольку на этом шаге необходимо получить только потенциально лучшую альтернативу. Чтобы помочь человеку сравнить две многокритериальные альтерна­тивы, можно воспользоваться принципом парной компенсации. Для этого необходимо разбить множество критериев на подмно­жества но 2-3 критерия в каждом. Если удастся показать, что по каждому такому подмножеству критериев одна альтернатива A₁ лучше другой А₂ (при фиксированных и одинаковых оценках по остальным критериям), то ее превосходство будет установлено (рис.3.1). Задача выбора лучшей альтернативы сведется тогда к нахождению такого разбиения множества критериев.

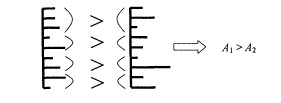
Рис.3.1. Сравнение многокритериальных альтернатив путем парной компенсации.

В рамках подхода вербального анализа решений был предложен но­вый человеко-машинный метод ШНУР (Шкала Нормализован­ных Упорядоченных Различий) для выбора лучшей из группы альтернатив, который имеет следующие особенно­сти. Прежде всего, и нем активно используются возможности компьютера, который без участия лиц, принимающих решение (далее ЛПР), попарно сравнивает все альтернативы по определенным правилам, анализируя их сход­ства и различия. При этом компьютер подготавливает наиболее эффективный процесс опроса ЛПР, что создает возможности для анализа большой группы альтернатив. Во-вторых, некото­рые количественные критерии (например, стоимость) также мо­гут рассматриваться как естественный и удобный язык выраже­ния предпочтений ЛПР. Метод позволяет работать как с каче­ственными, так и с количественными оценками альтернатив по критериям. Тем самым, метод ШНУР расширяет и дополняет возможности других методов вербального анализа решений.

Сравнивая все методы принятия решений, можно выделить следующие особенности метода ШНУР:

• В методе используются достаточно простые (с психологиче­ской точки зрения) процедуры выявления предпочтений ЛПР.

• Диалог ведется на понятном для ЛПР языке, причем рас­сматриваются как качественные, гак и количественные оценки альтернатив по критериям.

• Метод позволяет сравнить большое число альтернатив при минимальном числе вопросов к ЛПР.

• Метод позволяет приспособиться к конкретной задаче (на­бору альтернатив) и выделить лучшую или предположительно лучшую альтернативу.

• Метод позволяет ЛПР получить объяснения сделанному вы­бору путем предъявления тех его ответов, которые привели к полученному результату.

• Во многих случаях метод помогает ЛПР в выборе лучшей альтернативы. Однако метод не всегда приводит к нужному ре­зультату, т. к. альтернативы могут оказаться несравнимыми. В этом случае компьютерная система выдаст ЛПР следующую ин­формацию:

• показывает альтернативу с наибольшей суммой нормализо­ванных оценок как предположительно лучшую;

• сообщает, что имеются другие альтернативы, весьма близкие к лучшей; приводит оценки для этих альтернатив;

• предлагает ввести дополнительные критерии, по которых! можно различить альтернативы, которые не удалось сравнить данным методом;

• передает окончательный выбор на усмотрение ЛИР.

• Метод ШПУР является удобным для ЛПР, «прозрачных»» и действенным методом решения широкого круга задач.

Формальная постановка задачи, исходные данные, необходимые для её решения, варианты её решения

Постановка задачи выбора лучшей альтернативы

Сформулируем задачу выделения лучшей многокритериаль­ной альтернативы следующим образом.

Дано:

K={K₁,K₂...K_N} — множество критериев оценка альтернатив;

К = К^ U K^, где К^ — подмножество критериев, оценку по которым желательно максимизировать, К^ - минимизировать;

X_q={x^k_q} - множество оценок (шкала) y_j-го критерия, ко­торые упорядочены от лучшей (первой) к худшей (последней); |X_q|= 5_V. S_q — число значений оценок на шкале q-го критерия;

|X_q|=S_q, S_q — число значений оценок по шкале q-го критерия;

Y=X₁X₂…X_N— множество векторов вида у_j=(y_j1,y_j2,…,y_jN), где y_jqX_q, j=1,…,S, и S=|Y|=^N_q=1 S_q, задающие все гипотетические возможности альтернативы.

A={A₁,A₂,…,A_n} — множество реальных объектов, которо­му соответствует подмножествоY^aY, содержащее n векторов а_i = (a_i¹, a_i², ...,a_i^N), где a_i^q X_q;

V=V(A_i) — ценность альтернативы A_i для ЛПР. Пред­полагается, что ценность альтернативы обладает следующими свойствами: имеет максимальное и минимальное значения на множестве оценок Y; при независимых критериях значение цен­ности V(A_i) возрастает с улучшением оценки по каждому из критериев.

Требуется: на основе предпочтений ЛПР выделить из мно­жества А лучший объект, соответствующий наибольшему зна­чению априорно неизвестной функции ценности V(A_i).

B основу метода положены следующие допущения о возмож­ностях ЛПР:

• ЛПР может сравнивать по предпочтительности две альтер­нативы, отличающиеся оценками только по двум критериям;

• ЛИР может сравнивать по предпочтительности две альтер­нативы, отличающиеся более, чем по двум критериям, если при этом одна альтернатива предпочтительнее другой по одному критерию и уступает ей не более чем по трем критериям.

Сравнивая две альтернативы А₁ и А₂ ЛПР может дать один из трех возможных ответов:

• Альтернатива А₁ предпочтительнее альтернативы А₂.

• Альтернатива А₂ предпочтительнее альтернативы А₁.

• Альтернативы А₁ и А₂ одинаково предпочтительны.

При этом не предусматривается возможность ответа «Не знаю» или «Альтернативы несравнимы», поскольку считается, что ЛПР обладает сформулированными выше возможностям и всегда может ответить на простой вопрос.

Сделанные предположения о возможностях ЛПР имеют сле­дующие обоснования. Первое предположение многократно про­верялось при применении методов семейства ЗАПРОС. Оказалось, что люди достаточно последовательны и непро­тиворечивы при выполнении данной операции. В экспериментах наблюдались 2-6 противоречий при 50-60 сравнениях.

Второе предположение подвергалось проверке в работе. В ней получены подтверждении гипотез о том, что ЛПР может последовательно и непротиворечиво сравнивать объекты, отличающиеся оценками по тем критериям, а также что при независимости критериев сравнение предпочтительной оценки одной альтернативы с двумя-тремя предпочтительными оцен­ками другой альтернативы не создает чрезмерной нагрузки на кратковременную память.

Эти допущения положены в основу предлагаемой процедуры парного сравнения двух многокритериальных альтернатив по принципу парной компенсации. При сравнении делается попыт­ка уравновесить недостатки одной альтернативы недостатками другой, и в результате определяется, какая из двух альтер­натив обладает меньшими недостатками или большими досто­инствами.