
- •3. Обоснование методов рационального воздействия на атмосферу глубоких карьеров и принципов совершенствования средств и схем ее искусственного проветривания
- •3.1. Теоретические основы процессов искусственного проветривания карьеров
- •Значения коэффициента турбулентной структуры круглой свободной струи
- •Поправочный коэффициент на количество движения в начальном сечении струи
- •Сравнительная оценка энергозатрат на разрушение температурных инверсий в карьере «Удачный» тепловым и механическим способами
- •3.2. Обоснование рационального метода предупреждения и ликвидации опасных загрязнений внутрикарьерной атмосферы при отсутствии естественного воздухообмена
- •Требуемый уровень воздухообмена при нагнетательном проветривании некоторых глубоких карьеров [4, 11]
- •3.3. Обоснование рационального метода
- •3.4. Принципы совершенствования известных решений проблемы искусственного проветривания карьеров
Поправочный коэффициент на количество движения в начальном сечении струи
Условия образования и истечения струи |
Значения коэффициент а |
Цилиндрическая труба |
1,10÷1,20 |
Осевой вентилятор со спрямляющей решеткой |
1,40 |
Двухлопастный авиационный винт без кожуха |
1,52 |
То же, трехлопастный |
1,51 |
Четырехлопастный |
1,50 |
Пятилопастный |
1,49 |
Шестилопастный |
1,49 |
Восьмилопастный |
1,48 |
Соосные четырехлопастные винты встречного вращения |
1,25 |
Дальнобойность струи ограничивают сечением в котором средняя скорость снижается до критической икр . Обычно для горизонтальных струй принимают икр = 0,25 м/с, для вертикальных - икр = 0,6 м/с.
В условиях глубоких карьеров искусственно создаваемые турбулентные струи почти всегда неизотермичны по отношению к окружающей среде [107]. Причиной тому являются нагрев воздуха в вентиляционной системе и температурная неоднородность атмосферы, в которой развивается струя.
Траектория неизотермической струи искривляется под действием гравитационных объемных сил. На рис. 3.2 показана свободная подогретая струя, начальный угол истечения которой равен нулю. Горизонтальное направление струи сохраняется лишь на начальном участке. Она изгибается вверх и вновь выполаживается уже над карьером.

Рис. 3.2. Схема развития горизонтальной подогретой струи в карьере
Такой характер траектории струи объясняется различным соотношением кинетической энергии и энергии объемных сил в ней. На начальном участке ее кинетическая энергия настолько высока, что объемные силы не оказывают заметного влияния на движение.
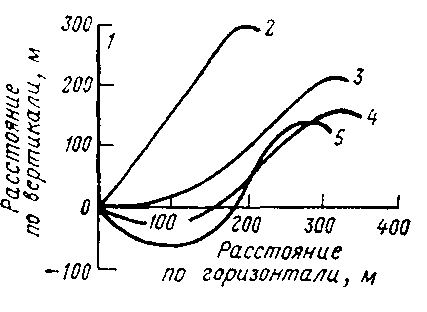
Рис.
3.3. Кривые траектории подогретой струи
при инверсии γ=-0,01 К/м: 1-α΄=90˚; 2-α΄=45˚;
3-α΄=0˚; 4-α΄=-20˚; 5-α΄=-45˚;
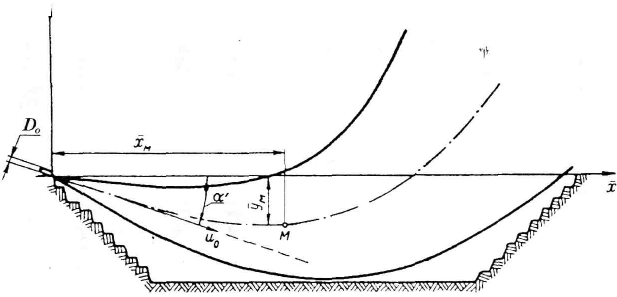
Уравнение оси неизотермической струи, развивающейся в безразлично равновесной атмосфере (рис. 3.4.), в безразмерных координатах имеет вид:
![]() ,
(3.5)
,
(3.5)
![]() .
.
![]() Рис.
3.4. Схема к расчету траектории
неизотермической струи
Рис.
3.4. Схема к расчету траектории
неизотермической струи
Уравнение (3.5) является универсальным. При подъеме оси струи к горизонту перед вторым членом уравнения ставится знак «+», при опускании — знак «-». При расчете охлажденной струи (Аг < 0) перед первым членом уравнения ставится знак«-».
В частном случае, когда а' = 0° (ось сопла горизонтальна), уравнение (3.5) принимает вид:
![]() ,
(3.6)
,
(3.6)
Скорость по оси изогнутой струи
![]() ,
м/с, (3.7)
,
м/с, (3.7)
где их – горизонтальная составляющая скорости,
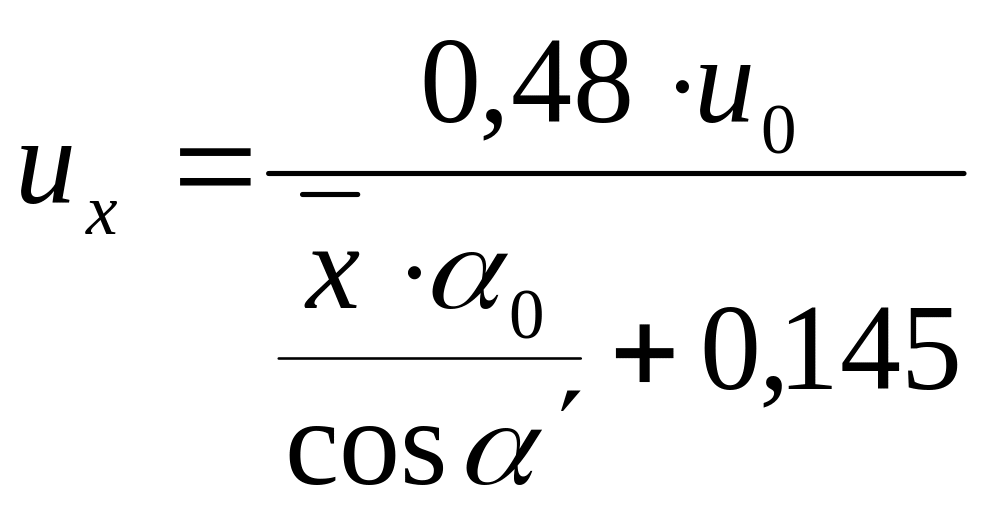 ,
м/с (3.8)
,
м/с (3.8)
где их – вертикальная составляющая скорости,
![]() ,
м/с
(3.9)
,
м/с
(3.9)
Температура по оси струи
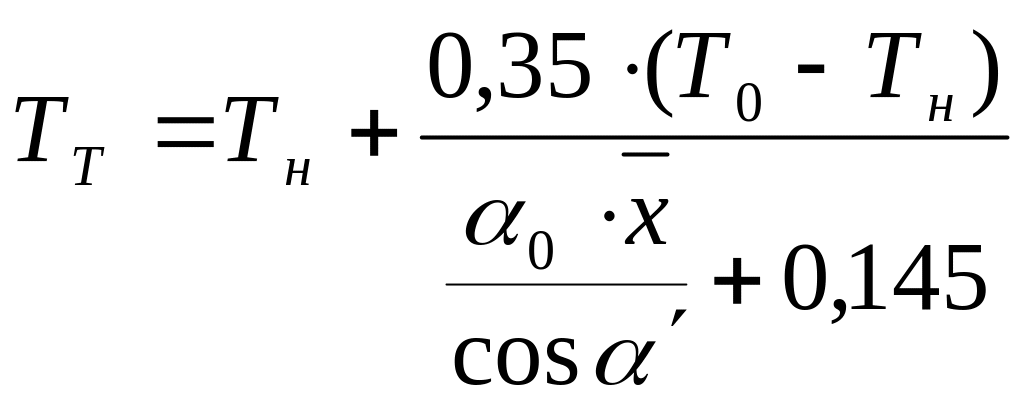 ,
К (3.10)
,
К (3.10)
Координаты точки перегиба оси струи следующие
![]() ;
(3.11)
;
(3.11)
![]() ;
(3.12)
;
(3.12)
Особый случай представляет собой расчет конвективных струй, генерируемых тепловыми установками. Известно, что при достаточной мощности теплового источника конвективный поток турбулентен и во многом сходен с неизотермической струей, вытекающей вверх с начальной скоростью [105].
Конвективная струя образуется вследствие передачи тепла от нагреваемого рабочего тела к прилегающим слоям воздуха, который, расширяясь, становится менее плотным и благодаря действию архимедовых подъемных сил, вытесняется более плотными объемами воздуха, подходящими радиально к нагретому телу.
Осевая скорость конвективного потока на высоте Н (м) от теплового источника при адиабатическом состоянии атмосферы определяется по формуле:
![]() ,
м/с, (3.13)
,
м/с, (3.13)
где W — количество конвективного тепла, отдаваемое источником в секунду, Вт. Тепловую мощность источника можно определить по формуле Ньютона [108]:
W=αт- FT ∙ ΔT, (3.14)
где αт — коэффициент теплообмена, Вт/(м2∙К); FT — площадь теплоотдающей поверхности, м2; ΔТ — температурный напор, К.
Расход воздуха в произвольном сечении конвективной струи
![]() ,
м3/с
(3.15)
,
м3/с
(3.15)
Одним из основных недостатков конвективных струй является низкий удельный весовой расход воздуха (отношение весового расхода к полной избыточной энергии в начальном сечении струи). Выполненное в работе [85] сравнение вертикальных турбулентных струй с различной степенью нагрева показало, что оптимальными по удельным энергетическим затратам во всех случаях являются менее нагретые (в идеальном — изотермические) струи возможно большего начального диаметра.
Точный учет термодинамического состояния атмосферы при расчете вентиляционных струй в карьере представляет значительную сложность, так как параметры воздуха в карьерном пространстве и вентиляционной струе в процессе проветривания изменяются не только по высоте, но и во времени.
Один из методов расчета струй с учетом термической стратификации атмосферы был разработан Ленинградским гидрометеорологическим институтом [4, 11].
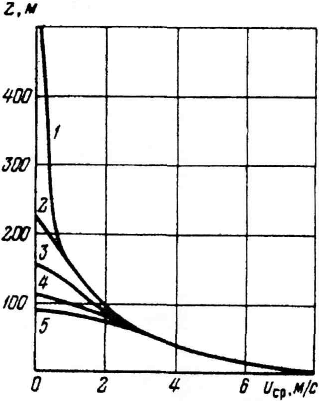
Графики, изображенные на рис. 3.5, показывают, как изменяется средняя скорость иср воздушной струи, создаваемой агрегатом АВК-3, в зависимости от высоты ее подъема г при различных величинах вертикального температурного градиента у. Из приведенных данных видно, что рабочая дальнобойность вертикальных струй при глубоких инверсиях (у = - 0,04 К/м) снижается по сравнению с дальнобойностью струй, распространяющихся в адиабатической атмосфере (у = 0,01 К/м) в 2÷2,2 раза. Дальнобойность конвективных струй снижается при тех же условиях в 5÷6 раз [4,7,11]. Поэтому целесообразна такая организация вентиляции, при которой существующая инверсия будет разрушена, а массы воздуха в карьере перейдут в неустойчивое состояние [3, 9].
Рис.
3.5. Изменение дальнобойности
струи вентилятора АВК-3 при
различной стратификации
атмосферы:
1-γ=0,01 К/м; 2-γ=0,006 К/м; 3-γ=0 К/м; 4-γ=-0,02 К/м;
5-γ=-0,04 К/м
Динамическое перемешивание воздушных масс в условиях внутрикарьерной температурной инверсии в конечном счете должно привести к ее разрушению и установлению адиабатического градиента в карьерном пространстве. Выделив в атмосфере карьера вертикальный столб воздуха, сделаем допущение, что перемешивание в нем происходит без тепло- и влагообмена с окружающей средой. После полного перемешивания воздуха в выделенном объеме установится постоянная потенциальная температура, равная средневзвешенному значению потенциальных температур в столбе от z = 0 (дно карьера) до z = Н (верхняя отметка карьера).
Зная распределение температуры воздуха по высоте до и после перемешивания, можно определить и соответствующие значения потенциальной энергии (для столба воздуха или для всего карьерного пространства).
Для столба воздуха высотой Н (м) до перемешивания потенциальная энергия определяется их следующего выражения:
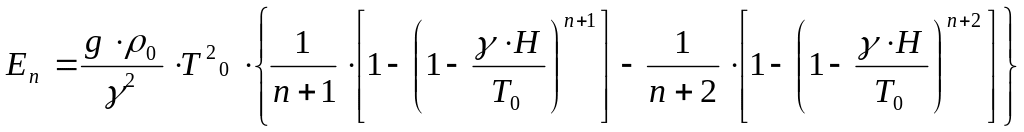 ,
Дж, (3.16)
,
Дж, (3.16)
гдеg=9,8 м/с2 — ускорение свободного падения; р0 и То — плотность (кг/м3) и температура (К) воздуха на уровне дна карьера; γ — вертикальный температурный градиент в атмосфере до перемешивания, К/м; п — показатель политропы (п =g/(γ∙R) - 1); R= 287,1 Дж/(кг∙К) — газовая постоянная для воздуха.
Для карьера в форме усеченного конуса с радиусом дна го (м) и углом откоса бортов α (град) величина потенциальной энергии воздуха до перемешивания
![]() ,
Дж,
(3.17)
,
Дж,
(3.17)
где
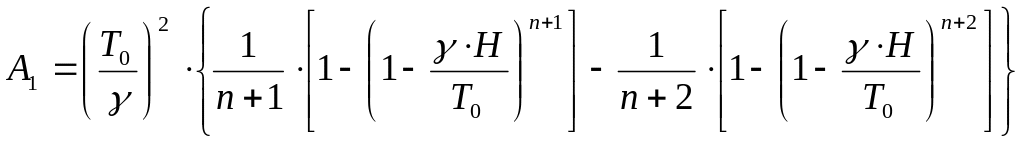 ;
(3.18)
;
(3.18)
![]()
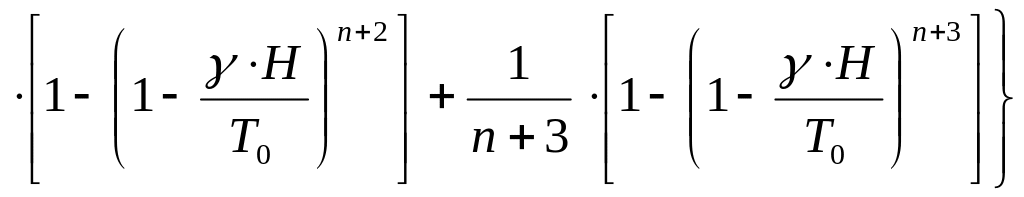 ;
(3.19)
;
(3.19)
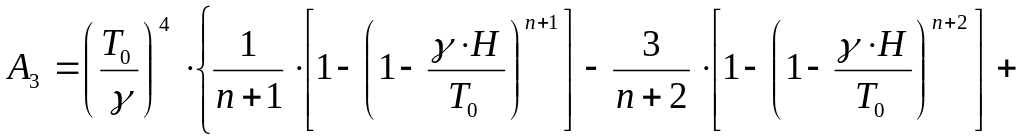
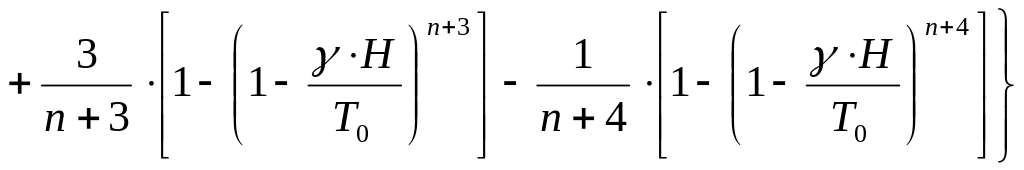 ;
(3.20)
;
(3.20)
Потенциальная энергия столба воздуха или всего карьерного пространства после перемешивания Е'n может быть определена по формуле (3.16) или (3.17) соответственно, при замене γ на γа = 0,01 К/м, То на Т'о, ро на р'о и n выражение g/(γа∙R) -1.
В результате перемешивания потенциальная энергия массы воздуха увеличится, а разница в значениях потенциальной энергии до и после перемешивания будет равна работе, затраченной на перемешивание.
Таким образом, энергия, необходимая для ликвидации инверсии в карьере механическим (динамическим) способом Емех, определится как разница между значениями потенциальной энергии массы воздуха в пределах карьерного пространства до и после перемешивания:
Емех= Е'п-Еn, Дж. (3.21)
Тогда время, необходимое для ликвидации инверсии, при отсутствии природных факторов, способствующих сохранению или разрушению инверсии, определится из выражения:
![]() ,
ч, (3.22)
,
ч, (3.22)
где N— мощность, затрачиваемая на перемешивание воздуха, кВт.
Энергетические затраты, необходимые для ликвидации температурных инверсий в карьерах методом динамического перемешивания Емех, довольно значительны. Однако энергозатраты при тепловом методе разрушения внутрикарьерных инверсий Етеп еще более велики. По оценкам А. А. Вершинина [109] Етеп/Емех≈7, а по данным института Якутнипроалмаз [39], приводимым в табл. 3.3, это отношение может составлять несколько десятков единиц.
Таблица 3.3
