1.3. Изучение динамики национального богатства с помощью статистических методов

Динамику национального богатства в основном изучают двумя статистическими методами: балансовым и методом анализа рядов динамики.

Полное представление о процессе воспроизводства основных фондов можно получить на основе балансового метода. В зависимости от цели исследования в практике статистики составляются балансы основных фондов двух видов: по полной первоначальной (балансовой) или полной восстановительной стоимости и по стоимости с учетом износа (первоначальной или восстановительной). Балансовый метод позволяет охарактеризовать процесс воспроизводства основных фондов по стоимости и натурально-вещественному составу и проанализировать их динамику в течение года (или за ряд лет при условии сопоставимости цен). Баланс по полной первоначальной или восстановительной стоимости характеризует названные процессы с позиции изменения количества (физического объема) основных фондов, а баланс по стоимости с учетом износа — изменение их стоимости с учетом физического состояния. Упрощенная схема баланса основных фондов по полной первоначальной (полной восстановительной) стоимости представлена на схеме 1.

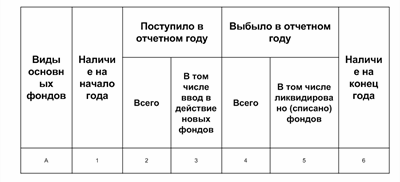
Схема 1.Баланс основных фондов по полной стоимости

Для характеристики изменения в течение года стоимости основных фондов разрабатываются балансы основных фондов по остаточной стоимости (первоначальной или восстановительной с учетом износа). В них все показатели основных фондов (кроме ввода в действие) учитываются по стоимости с учетом износа, а также отражаются два дополнительных показателя: капитальный ремонт (+) и амортизация (-).Баланс основных фондов по остаточной стоимости (первоначальной или восстановительной с учетом износа) представлен на схеме 2.

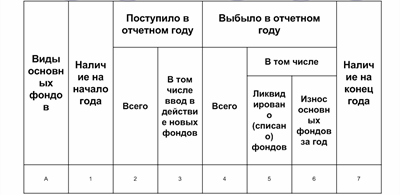
Схема 2.Баланс основных фондов по остаточной стоимости

В отличие от баланса основных фондов по полной стоимости, отражающего процесс воспроизводства основных фондов в их физическом объеме, баланс основных фондов по стоимости за вычетом износа (остаточной стоимости) призван охарактеризовать изменение в течение года реальной стоимости фондов не только под влиянием ввода в действие и выбытия по ветхости и износу, но и с учетом частичного восстановления их стоимости путем капитального ремонта и с учетом амортизации. Баланс основных фондов по остаточной стоимости тесно связан с балансом капитальных вложений, отражающим процесс выделения и степень освоения капитальных вложений на капитальное строительство и капитальный ремонт в течение года. Наиболее точные результаты при оценке национального богатства и его отдельных элементов может дать перепись (генеральная инвентаризация), которая является весьма трудоемкой и дорогостоящей процедурой. Поэтому в большинстве стран используются различные методы косвенных расчетов и построения динамических рядов. Анализ интенсивности изменения во времени осуществ­ляется с помощью показателей, получаемых в результате срав­нения уровней, к таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.

Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.

Показатели анализа динамики могут вычисляться на по­стоянной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с кото­рым производится сравнение, — базисным.

Для расчета показателей анализа динамики на постоян­ной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляе­мые при этом показатели называются базисными.

Для расчета показателей анализа динамики на перемен­ной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными.

Важнейшим статистическим показателем анализа дина­мики является абсолютное изменение — абсолютный прирост.

Абсолютное изменение характеризует увеличение или уменьшение уровня ряда за определенный промежуток време­ни. Абсолютный прирост с переменной базой называют скоро­стью роста.

Абсолютный прирост Абсолютный прирост

(цепной): (базисный):

где у_i - уровень сравниваемого периода;

y_{i -1} - уровень предшествующего периода;

y₀ - уровень базисного периода.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени ( ).

Для характеристики интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста. Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному. Темпы роста всегда представляют собой положительное число.

Темп роста (цепной): Темп роста (базисный):

Т_р^ц = % Т_р^б = %

Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста.

Темп прироста показывает, на сколько про­центов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения.

Темп прироста может быть положительным, отрицатель­ным или равным нулю.

Темп прироста (цепной): Темп прироста (базисный):

Т_пр^ц = % Т_пр^б = %

можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%.

Т_пр = Тр – 100 %.

При анализе динамики развития следует также знать ка­кие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при сниже­нии (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показа­телем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:

Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня. Оно показы­вает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.

А% =

Для более глубокого понимания характера явления необхо­димо показатели динамики анализировать комплексно, совместно.

Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средние уровни ряда и средние показатели изменения уровней ряда.

Средний уровень ряда характеризует обобщённую величину абсолютных уровней. Он рассчитывается по средней хронологи­ческой, т.е. по средней исчисленной из значений, изменяющих­ся во времени.

где y_1,….. y_n - абсолютные уровни ряда; n - число уровней ряда.

Обобщающий показатель скорости изменения уровней во времени - средний абсолютный прирост. Он показывает среднюю величину ежегодных приростов.

Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит - средний темп роста, показывающий во сколько раз в среднем за единицу времени изменился уровень ряда динамики. Средний темп роста – это обобщающая характеристика индивидуальных темпов роста ряда динамики.

Средние темпы прироста рассчитываются на основе средних темпов роста, вычитанием из последних 100%.

Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100%, а средний темп прироста – отрицательной величиной.