Корреляционная решетка зависимости принадлежности образцов к старичной (а) или пойменной ( ) фации аллювия при проявлении черного (в) или любого другого ( ) цвета.

	A
B	32	26	=58
	6	118	=124
	=38	=144

Для иллюстрации техники вычислений тетрахорического показателя связи рассмотрим результаты определения в n = 182 точках генетической принадлежности аллювия к старичной (А) или пойменной ( )фации, и цвета образцов - черного (В) или любого другого ( ). Учитывая, что при наличии образцов старичной фации в случаях, черный цвет грунты имели в случаях (табл. 9.9.2). При взаимной независимости этих событий частота их совместной встречи должна была бы быть , а это меньше эмпирической частоты , таким образом, можно ожидать, что сравниваемые явления не независимы.

Поскольку , наименьшая из всех четырех теоретических частот, больше 5, то допустима проверка значимости связи с помощью χ². По формуле (9.9.1): . Формулы (9.9.2) и (9.9.3) дают значения χ² соответственно 57,6 и 60,6, что существенно выше даже для α = 0,005, поэтому каких-либо сомнений в наличии связи здесь быть не может.

Следует заметить, что могут достигать своих крайних значений +1 и -1 лишь в случаях, когда и соответственно, . В рассмотренном примере принципиально невозможно получить , поскольку черный цвет у образцов грунта встречен в 58 случаях, а старичный аллювий - только в 38. Если бы даже все события А произошли при условии наличия события В, и , мы получили бы .

В тех случаях, когда один или оба признака измерены на количественных шкалах, альтернативные классы одного из признаков можно выделить таким образом, чтобы было обеспечено равенство . Допустим, признак А, измеренный на классификационном уровне, среди n измерений был обнаружен в числе случаев. Если второй признак В, измеренный на количественной шкале, предпочтительно связан с А таким образом, что наличию А соответствуют более высокие значения, то числу случаев наличия А должно соответствовать равное ему число наиболее высоких значений признака В, которые и составят класс В по этому признаку. К классу будут отнесены все остальные более малые значения. Например, в ранжированной последовательности признака х граничным значением, разделяющим классы B и будет γ-квантиль х_(γ), где , - доля значений х_i больших х_(γ) при условии . Тогда событием В будет , а .

Если частоты и одинаковы, то одинаковы и частоты и . В этом случае, сохраняя обозначение п для объема четырехклеточной таблицы и - для частоты совместных событий А и В, и принимая обозначения , получим более простое выражение для формулы (9.9.1):

. 9.9.4)

Так, если среди п = 100 образцов кубической формы с ребром 2 см в пределах дисперсной зоны коры выветривания крупные карбонатные стяжения (А) были обнаружены в = 16 случаях, и резонно допустить, что именно этим образцам должно соответствовать наибольшее содержание карбонатов (событие В), то, принимая и имея и , можно вычислить квантиль х_(0,84) по формуле (3.4.3), который оказался равным 17,9 %. После подсчета частот четырехпольная таблица обрела следующий вид:

Таблица 9.9.3.

Корреляционная таблица связи наличия крупных стяжений (А) с содержанием СаСО₃ более х_(0,84) = 17,9 % (В).

	A
B (x > 17,9)	9	7	16
	7	77	84
	16	84	100

Подставляя в формулу (9.9.3) соответствующие значения, получим:

.

9.10. Несимметричные меры ассоциации. Тетрахорический показатель связи относится к центрированным симметричным показателям (ноль - отсутствие связи, пределы колебаний от -1 до +1). Его можно трактовать и как меру приуроченности появления одного признака к наличию второго (и второго к первому), и как меру связи между отсутствием одного признака и отсутствием второго, так как .

Однако существуют явления, связь между которыми не имеет симметричного характера. Такого рода связи могут оцениваться несимметричными мерами ассоциации. Весьма часто в качестве несимметричной меры ассоциации используется коэффициент Дайса:

, (9.10.1)

показывающий, насколько наличие признака В влечет за собой появление события А. Соответственно коэффициент

(9.10.2)

отражает ассоциированность события В с событием А. В этих формулах и - частоты появления событий A и В среди п испытаний, - частота совместного их появления (см. табл. 9.9.1). Коэффициент Дайса нецентрирован. Например, соответствует "отрицательной ассоциации" событий: при наличии В событие А отсутствует. Если события В и А независимы друг от друга, . При наличие признака В однозначно вызывает появление признака А.

Оценки коэффициентов Дайса имеют дисперсии:

(9.10.3)

и

. (9.10.4)

Принимая во внимание, что повторности при оценках подобных мер ассоциации обычно исчисляются десятками и более, допустимо считать, что ошибкам, полученным по формулам (9.10.3-9.10.4), соответствует число степеней свободы . При необходимости эти ошибки можно использовать для нахождения доверительных интервалов KD.

Обращаясь к ранее рассмотренным данным, представленным в табл. 9.9.2, получим два коэффициента Дайса: и , из которых следует, что наличие черного цвета грунта (В) практически не влияет на то, будет ли он относится к старичной фации аллювия, поскольку близок к 0,5, соответствующему отсутствию ассоциированности. В то же время предпочтительность наличия черного цвета у образцов старичного аллювия не вызывает сомнений.

Из рассмотренного примера видно, что коэффициенты Дайса неудобны для интерпретации из-за своей нецентрированности. В связи с этим более удобно пользоваться их центрированной модификацией, так называемым трансформированным коэффициентом Дайса - TKD. Для оценки меры ассоциированности признака А с признаком В TKD может быть вычислен по формулам (обозначения см. в табл. 9.9.1):

, (9.10.5)

или

. (9.10.6)

Соответственно, для нахождения меры ассоциации признака В с признаком А получим:

, (9.10.7)

или

. (9.10.8)

Очевидно, что между TKD и KD существует связь очень простого вида:

TKD = 2KD - 1.

Удобство TKD как меры ассоциации заключается в том, что этот коэффициент, так же как коэффициент корреляции r и r_s, как показатель связи r_B, может меняться в интервале значений от -1 до +1. Эти крайние значения соответствуют либо непременному отсутствию одного признака при наличии другого (TKD = -1), либо обязательному присутствию первого, если второй есть (TKD = +1). Нулевое значение TKD соответствует отсутствию зависимости появления одного признака от наличия второго.

Проверка значимости зависимостей, измеряемых TKD (и KD), может приближенно осуществляться с помощью χ², вычисляемых по формулам:

, (9.10.9)

для зависимости наличия А от наличия В и

, (9.10.10)

для зависимости В от А. Если для ν = 1, то с уровнем значимости α гипотеза о независимости отвергается. Для данных, представленных в табл. 9.9.2, будем иметь (по формуле 9.10.5) и (по формуле 9.10.8) . Соответственно (формулы 9.10.9-9.10.10) для зависимости А/В: , а для зависимости В/А: . Поскольку для ν = 1, и , можно заключить, что о какой-либо зависимости А от В говорить не приходится, а обратная зависимость статистически весьма значима. Это проявляется и в значениях TKD, мало отличного от нуля для и достаточно высокого у .

9.11. Моделирование свойств геологических объектов с помощью случайных функций. При решении многих инженерно-геологических задач возникает необходимость количественной оценки пространственной изменчивости показателей свойств грунтов. Методы статистики случайных величин для этих целей малопригодны, так как все статистические модели не учитывают пространственного расположения точек наблюдений. С этой целью может быть использован математический аппарат теории случайных функций.

Случайной называется такая функция, которая в результате опыта может принять тот или иной конкретный вид, причем неизвестно заранее, какой именно. Аргументами при этом могут быть время (случайные процессы) или координаты пространства (случайные поля или последовательности).

Случайные процессы используются в качестве моделей прибрежно-морских гидродинамических процессов, для описания сезонных колебаний уровней грунтовых вод, при изучении гидродинамических свойств пород, при опытных откачках из скважин и т. п. Гораздо чаще приходится иметь дело с моделями случайных полей и последовательностей, описывающих пространственную изменчивость самых различных инженерно-геологических признаков в одномерном, двумерном или трехмерном пространствах.

К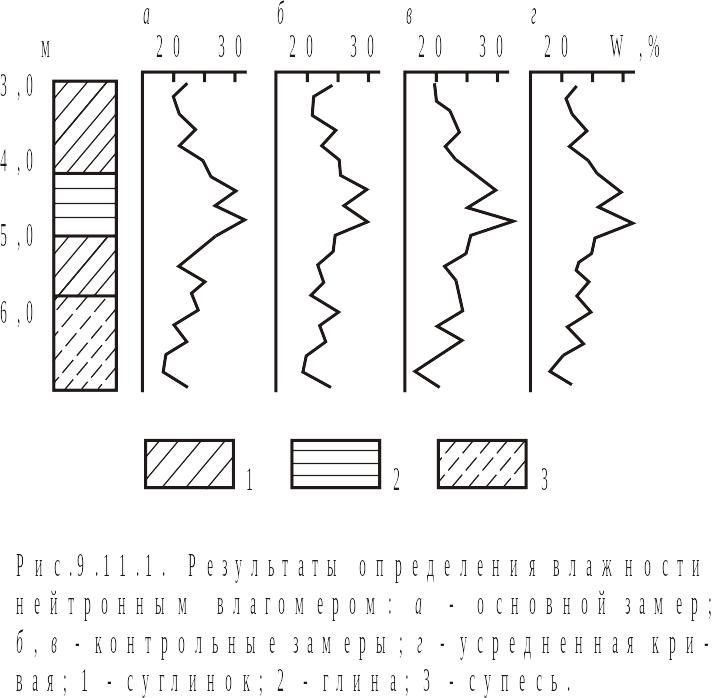 онкретный вид, который принимает функция в результате опыта, называется ее реализацией. Так, например, диаграмма изменения значений любого показателя по скважине может рассматриваться как реализация случайной функции, описывающей изменение изучаемого свойства грунта на пробуренном интервале. Совокупность нескольких контрольных диаграмм образует семейство или ансамбль реализации случайной функции (рис.9.11.1). Каждая реализация отражает общие тенденции в изменении изучаемого свойства, но они несколько отличаются друг от друга вследствие аппаратурных погрешностей, несовпадения точек замеров и других случайных факторов.

Совокупность значений случайной функции Х = f (l) при любом фиксированном значении аргумента l называется сечением случайной функции и является обычной случайной величиной (рис.9.11.1), т. е. совмещает в себе черты случайной величины и функции. Если зафиксировать значение аргумента, она превращается в обычную случайную величину, а отдельная реализация может рассматриваться как обычная (неслучайная) функция.

Модель типа случайной функции, как и статистическая, основана на положениях теории вероятностей. Процесс моделирования сводится в конечном итоге к получению выборочных значений и к их статистической оценке путем проверки статистических гипотез с помощью критериев согласия. При оперировании со случайными функциями широко используются основные понятия математической статистики о функциях и моментах распределения, уровнях значимости и доверительных вероятностях событий.

Главными характеристиками случайной функции являются ее математическое ожидание М_x(l), дисперсия D_x(l) и корреляционная функция K_x(l). В отличие от числовых характеристик случайных величин, представляющих собой определенные числа, характеристики случайных функций представляют собой не числа, а функции. Математическим ожиданием случайной функции Х_x(l) называется неслучайная функция М_x(l), которая при каждом значении аргумента l равна математическому ожиданию соответствующего сечения случайной функции. Оценка математического ожидания по ансамблю из N реализаций рассчитывается по формуле:

(9.11.1)

и является геометрическим местом точек средних значений изучаемого свойства по сечениям. В приведенном примере (см. рис.9.11.1) оценкой математического ожидания служит усредненная диаграмма влажности грунтов, рассчитанная по трем реализациям. При изучении случайных многократно повторяющихся процессов оценкой математического ожидания является усредненный график параметра процесса, построенный путем расчета средних значений этого параметра для фиксированных значений расстояния или интервалов времени с начала процесса.

Дисперсией случайной функции X(l) называется неслучайная функция D_x(l), значения которой для каждого l равны дисперсии соответствующего сечения случайной функции. Она характеризует ширину полосы разброса возможных реализации случайной функции относительно ее математического ожидания. Оценка дисперсии случайной функции рассчитывается по формуле:

. (9.11.2)

Для описания основных свойств случайной функции математического ожидания и дисперсии недостаточно. Ни одна из данных характеристик не отражает особенностей внутренних связей между отдельными сечениями такой функции. С этой целью используется специальная характеристика - корреляционная функция, отражающая степень зависимости между сечениями случайной функции при различных l.

Корреляционной функцией случайной функции X(l) называется неслучайная функция двух аргументов K_x(l', l''), которая при каждой паре значений аргумента равна корреляционному моменту соответствующих сечений случайной функции:

, (9.11.3)

где и - значения центрированной случайной функции при значениях аргумента l' и l''. Центрирование случайной функции осуществляется путем вычитания из значений случайной функции ее математического ожидания:

. (9.11.4)

В частном случае, когда оба аргумента случайной функции совпадают, т. е. , корреляционная функция K_x(l', l'') обращается в дисперсию случайной функции:

. (9.11.5)

При использовании случайных функций инженерно-геологические объекты рассматриваются как случайные поля, состоящие из элементарных участков, каждый из которых сответствует зоне экстраполяции единичного наблюдения. В пределах каждого элементарного участка изучаемое свойство рассматривается как случайная величина, изменяющаяся относительно некоторого ее среднего значения. Изменения математических ожиданий и дисперсий этих случайных величин можно описать неслучайными функциями координат центров элементарных участков и рассматривать эти функции как математическое ожидание и дисперсию случайной функции.

Упорядоченный ряд значений признака, полученных путем опробования по заданному направлению в определенных точках внутри данного поля, представляет собой одну из возможных реализации случайной функции, аргументом которой является расстояние между точками наблюдений. Группа точечных значений параметра, расположенных в одной плоскости, представляет собой реализацию плоскостного сечения случайного поля, а вся совокупность точечных замеров - одну из его объемных реализации. Такая модель отражает не только специфику природной изменчивости инженерно-геологических объектов, но и методику их изучения. Модели одного того же участка, построенные по совокупности экспериментальных данных, могут существенно различаться в зависимости от объема проб и густоты сети наблюдений. Для описания изменчивости любого свойства практически достаточно знать характеристики случайных функций по трем взаимно ортогональным направлениям, совпадающим с осями анизотропии природных геологических тел.

Для описания характера изменчивости двумерных инженерно-геологических тел (массивов) используют двумерную автокорреляционную функцию (ДАКФ), которая выражает силу корреляционной связи между значениями признака в точках поля, расположенных на разном расстоянии друг друга относительно двух координат пространства Х и Y.

Использование аппарата теории случайных функций для решения инженерно-геологических задач сопряжено с рядом сложностей и ограничений. Главное из них заключается в том, что такая функция, подобно случайной величине, является совокупностью частных реализации, в то время как результаты наблюдений чаще всего представляют собой единственную реализацию случайной функции. Оценка случайной функции по одной реализации возможна только в том случае, если она обладает свойствами стационарности и эргодичности. Функции же, характеризующие наблюдаемую изменчивость свойств природных геологических образований, как правило, не обладают этими свойствами. Поэтому при использовании моделей типа случайных функций вводится ряд допущений. Для расчета важнейших характеристик эмпирических случайных функций необходимо обеспечить массовость исходных экспериментальных данных, поэтому широкое применение модели рационально только в тех случаях, когда количество единичных наблюдений достаточно велико, а их плотность обеспечивает отчетливое проявление автокорреляции наблюдаемых значений признака.

Случайная функция Х(1) называется стационарной, если все ее вероятностные характеристики не зависят от l (точнее, не изменяются при любом сдвиге аргументов по оси l). Такая функция отличается постоянством математического ожидания и дисперсии и зависимостью ее корреляционной функции не от двух аргументов, а только oт расстояния r между первым и вторым аргументами: .

Корреляционная функция стационарной случайной функции выражается через корреляционный момент соответствующих сечений случайной функции и характеризует степень связи между ними в зависимости oт значений аргумента. В общем виде она может быть выражена формулой:

, (9.11.6)

где L - длина исследуемого профиля (участка); r - расстояние между точками наблюдений, выраженное числом интервалов между ними; f(x_i) - переменная величина (например, значения плотности грунта в ряду, который начинается значением x₁ и заканчивается значением х_n-r); f(x_i+r) - переменная величина (например, значение плотности грунта в ряду, который начинается значением x_i+r и заканчивается значением х_n; M_х - среднее значение переменной величины f(x) в интервале от 0 до L.

На практике часто пользуются корреляционной функцией, нормированной по дисперсии . Значения функции ρ_x(r) представляют собой коэффициенты корреляции между сечениями случайной функции, разделенными расстояниями r. Очевидно, что значение ρ_x(0) равно 1.

Для количественного описания характера изменчивости стационарных случайных функций используется также структурная функция (вариограмма), которая рассчитывается через квадраты разностей значений признака в точках, отстоящих друг от друга на расстояние r:

. (9.11.7)

Между структурной и корреляционной функциями существует почти строгая зависимость при r заведомо меньшем, чем .

Корреляционная функция стационарной случайной функции постепенно убывает с увеличением аргумента до определенного его значения, называемого пределом корреляции, и равна нулю при значениях аргумента, больших предела корреляции (рис.9.11.2, а). Ее структурная функция возрастает в том же интервале значений r, а при расстоянии, большем предела корреляции, равна удвоенному значению статистической дисперсии исследуемого свойства (рис.9.11.2, б).

При расчетах эмпирических корреляционных и структурных функций интегралы заменяются суммами, поскольку сеть наблюдений дискретна. При равномерной дискретной сети наблюдений эмпирические корреляционные и структурные функции рассчитываются по формулам:

, (9.11.8)

, (9.11.9)

где i - порядковый номер замера в исследуемом ряду значений х; п - общее число замеров; r - последовательно принимает значения 1, 2, 3, ..., (п-1).

Расчет значений эмпирической нормированной корреляционной функции заключается в вычислении коэффициентов корреляции между значениями исследуемого ряда с порядковыми номерами от 1 до (n - r) и значениями того же ряда, сдвинутыми относительно исходного на r значений, т. е. ряда с порядковыми номерами от r до п.

Пример расчета первой точки нормированной корреляционной функции по результатам определения влажности флювиогляциальных суглинков нейтронным влагомером в скважине (см. рис.9.11.2) приведен в табл.9.11.1.

Если одна реализация стационарной случайной функции на достаточно большом интервале эквивалентна большому числу реализации на ограниченном интервале, считается, что функция обладает эргодическим свойством. В этом случае ее среднее значение на достаточно большом участке приближенно равно среднему по множеству наблюдений. Различают два подкласса стационарных случайных функций - эргодические и неэргодические.

Таблица 37.