Вступ
Значна кількість задач машинобудування пов’язана із розв’язанням складних математичних задач, які вимагають виконання складних розрахунків та застосування чисельних методів. Для ефективного розв’язання таких задач доцільне застосування існуючих програмних середовищ, таких як Mathcad та MathLab.
Mathcad є розробкою компанії MathSoft Inc і представляє легку для засвоєння систему математичних розрахунків, причому, всі обчислення записуються у традиційній математичній нотації.
Система MATLAB розроблена фірмою MathWorks і представляє собою інтерактивне середовище для обчислень та моделювання. Сильна сторона системи – робота з матрицями і векторами. Система має величезний набір вбудованих функцій, а також є можливість створювати призначені для користувача функції. У системі дуже якісно реалізована побудова двох і тривимірних зображень. Крім того, є бібліотека, яка забезпечує зручне управління виконанням програм, а також доповненнями, - наприклад мова Simulink моделювання нелінійних динамічних систем.
Методичні вказівки присвячені основам роботи в зазначених програмних середовищах та спрямовані на покращення засвоєння теоретичного матеріалу і здобуття студентами практичних навичок.
Тема 1 Наближені обчислення
Визначення
1.
Абсолютною похибкою
називається величина, не менша за
абсолютне значення різниці між точним
числом А и його наближеним значенням а
:
,
отже
або це можна записати
.
Визначення
2.
Відносною похибкою
називається
величина:
або
.
Визначення 3. Значущими цифрами числа називаються всі цифри крім нулів, що стоять лівіше першої відмінної від нуля цифри. Нулі, що записані у кінці числа завжди є значущими. Наприклад числа 0,001407 і 5,0200 представлені відповідно 4 та 5 значущими цифрами. Форма запису у вигляді 0,1407·10-2 називається нормальною.
Визначення
4. Цифри
наближеного числа а
називаються вірними у сенсі
,
якщо абсолютна похибка не перевищує
одиниць розряду останньої вірної цифри:
.
При
цифри
називаються вірними у широкому сенсі,
при
– у вузькому сенсі.
,
.
Правило виконання операцій з наближеними числами.
виділяють число з найкоротшим десятковим записом;
інші числа округляють, лишаючи один або два знаки відносно довжини найкоротшого числа;
виконують арифметичну операцію із збереженням всіх цифр;
отриманий результат округляють до найкоротшого числа.
Похибки арифметичних операцій:
Арифметична операція |
Функція |
Похибка |
сума, різниця |
|
|
добуток |
|
|
частка |
|
|
степінь |
|
|
корінь |
|
|
.
,
Обернена
задача:
визначити припустиму похибку аргументів,
так, що б похибка функції не перевищувала
заданого числа
.
Для цього накладається вимога, що внесок
кожного доданку є однаковим:
–
принцип рівного впливу. Тоді:
або
,
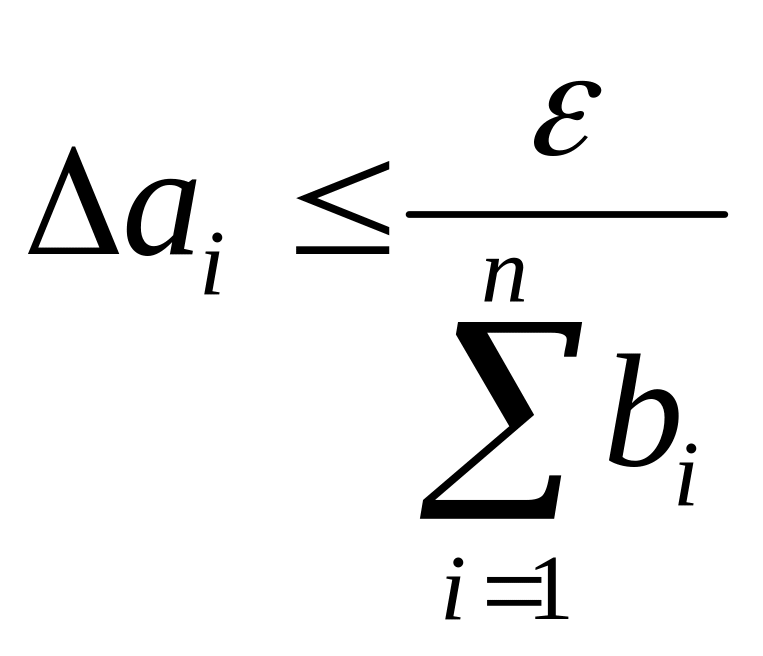Типові задачі.
Задача
1.1. Обчислити
значення
,
де
,
,
,
та
визначити абсолютну похибку результату.
Розв’язок.
Найкоротше
число має два знаки після десяткової
коми, то будемо виконувати обчислення
до четвертого знаку. Зробимо необхідні
установки в опціях обчислень та виводу
результату середовища Mathcad.
Так як похибка
перевищує 1. то далі можна виконувати
обчислення з округленням до 2-го знаку.
Результати занесемо у таблицю:
|
|
|
|
|
|
|
|
|
|
|
8,53 |
6,271 |
1,141 |
12,48 |
14,801 |
1943,765 |
28769.666 |
4,564 |
6303.608 |
|
0,002 |
0,0005 |
0,0005 |
0,004 |
0,0025 |
1,87 |
31,647 |
0,0005 |
9,45541 |
|
0,0002 |
0,0001 |
0,0004 |
0,0003 |
0,0002 |
0,0009 |
0,0011 |
0,0004 |
0,0015 |
Результат
можна округлити до цілих:
.
Задача
1.2. Обчислити
значення
та оцінити абсолютну похибку, взявши
значення аргументів з чотирма вірними
числами.
Розв’язок.
Визначимо аргументи:
,
.
,
.
Обчислимо
наближене значення функції:
Абсолютна
похибка функції:
,
де
,
,
.
Отже абсолютна похибка результату:
і три вірних знаки.
Завдання 1 Обчислити значення виразу в середовищі Mathcad, оцінити абсолютну та відносну похибки. Результат округлити і записати з точністю до абсолютної похибки.
№ 1.
1)
;
2)
;
3)
1) |
1 |
2 |
3 |
|
3) |
1 |
2 |
3 |
||
|
3,85±0,01 |
4,16±0,005 |
7,27±0,01 |
|
|
1,141 |
2,234 |
5,813 |
||
|
2,0435±0,0004 |
12,163±0,002 |
5,205±0,002 |
|
|
3,156 |
4,518 |
1,315 |
||
|
962,6±0,1 |
55,18±0,01 |
87,32±0,03 |
|
|
1,14 |
4,48 |
2,56 |
||
2) |
|
|
|
|
|
|
||||
1 |
4,3±0,05 |
17,21±0,02 |
8,2±0,05 |
12,417±0,003 |
8,37±0,005 |
|
||||
2 |
5,2±0,04 |
15,32±0,01 |
7,5±0.05 |
21,823±0,002 |
7,56±0,003 |
|
||||
3 |
2,13±0,01 |
22,16±0,03 |
6,3±0,04 |
16,825±0.004 |
8,13±0,002 |
|
||||
1.
2.
3.
№ 2.
1)
;
2)
;
3)
;
1) |
4 |
5 |
6 |
|
3) |
4 |
5 |
6 |
||
|
228,6±0,06 |
315,6±0,05 |
186,7±0,04 |
|
|
8,53 |
6,44 |
9,05 |
||
|
86,4±0,02 |
72,5±0,03 |
66,6±0,02 |
|
|
6,271 |
5,323 |
3,244 |
||
|
67,7±0,05 |
53,8±0,04 |
72,3±0,03 |
|
|
12,48 |
15,44 |
20,18 |
||
2) |
|
|
|
|
|
|
||||
4. |
13,5±0,02 |
3,7±0,02 |
4,22±0,004 |
34,5±0,002 |
23,725±0,005 |
|
||||
5. |
18,5±0,03 |
5,6±0,02 |
3,42±0.003 |
26,3±0,01 |
14,782±0,006 |
|
||||
6. |
11,8±0,02 |
7,4±0,03 |
5,82±0,005 |
26,7±0,03 |
11,234±0,004 |
|
||||
4.
5.
6.
№ 3.
1)
;
2)
;
3)
;
1) |
7. |
8. |
9. |
|
3) |
7. |
8. |
9. |
|
3,845±0,004 |
4,632±0,003 |
7,312±0,004 |
|
|
0,562 |
0,834 |
0,445 |
|
16,2±0,05 |
23,3±0,04 |
18,4±0,03 |
|
|
0,2518 |
0,3523 |
0,4834 |
|
10,8±0,1 |
11,3±0,06 |
20,2±0,08 |
|
|
0,68 |
0,74 |
0,87 |
2) |
|
|
|
|
|
7. |
2,754±0,001 |
11,7±0,04 |
0,56±0,005 |
10,536±0,002 |
6.32±0,008 |
8. |
3,236±0,002 |
15,8±0,03 |
0,64±0,004 |
12,415±0,003 |
7,18±0,006 |
9. |
4,523±0,003 |
10,8±0,02 |
0,85±0,003 |
9,318±0,002 |
4,17±0,004 |
7.
8.
9.в)
№ 4.
1)
;
2)
;
3)
;
1) |
10 |
11 |
12 |
|
3) |
10 |
11 |
12 |
|
3,456±0,002 |
1,245±0,001 |
0,327±0,005 |
|
|
8,51 |
5,71 |
7,28 |
|
0,642±0,0005 |
0,121±0,0002 |
3,147±0,0001 |
|
|
23,42 |
32,17 |
11,71 |
|
7,12±0,004 |
2,43±0,003 |
1,78±0,001 |
|
|
3,81 |
2,42 |
5,31 |
2) |
|
|
|
|
|
10. |
23,16±0,02 |
11,7±0,005 |
145,5±0,08 |
28,6±0,1 |
0,28±0,006 |
11. |
17,41±0,01 |
1,27±0,002 |
342,3±0,04 |
11,7±0,1 |
0,71±0,003 |
12. |
32,37±0,03 |
2,35±0,001 |
128,7±0,02 |
27,3±0,04 |
0,93±0,001 |
10.
11.
12.
№ 5.
1)
;
2)
;
3)
;
1) |
13 |
14 |
15 |
|
3) |
13 |
14 |
15 |
|
0,643±0,0005 |
0,142±0,0003 |
0,258±0,0002 |
|
|
21,1 |
17,8 |
32,5 |
|
2,17±0,002 |
1,71±0,002 |
3,45±0,001 |
|
|
22,08 |
32,47 |
27,51 |
|
5,843±0,001 |
3,727±0,001 |
7,221±0,003 |
|
|
31,11 |
11,42 |
21,78 |
2) |
|
|
|
|
|
13. |
27,16±0,006 |
5,03±0,01 |
3,6±0,02 |
12,375±0,004 |
86,2±0,05 |
14. |
15,71±0,005 |
3,28±0,02 |
7,2±0,01 |
13,752±0,001 |
33,7±0,03 |
15. |
12,31±0,004 |
1,73±0,03 |
3,7±0,02 |
17,428±0,003 |
41,7±0,01 |
13.
14.
15.
№ 6.
1)
;
2)
;
3)
;
1) |
16 |
17 |
18 |
|
3) |
16 |
17 |
18 |
||
|
0,3575±0,0002 |
0,1756±0,0001 |
0,2731±0,0003 |
|
|
2,456 |
7,751 |
5,441 |
||
|
2,63±0,01 |
3,71±0,03 |
5,12±0,03 |
|
|
22,08 |
3,35 |
6,17 |
||
|
5,854±0,0005 |
0,285±0,0002 |
0,374±0,0001 |
|
|
|
|
|
||
2) |
|
|
|
|
|
|
||||
16. |
16,342±0,001 |
2,5±0,03 |
38,17±0,002 |
9,14±0,005 |
3,6±0,04 |
|
||||
17. |
12,751±0,03 |
3,7±0,02 |
23,78±0,003 |
8,12±0,004 |
1,7±0,01 |
|
||||
18. |
31,456±0,002 |
3,3±0,01 |
33,28±0,003 |
6,71±0,001 |
5,8±0,02 |
|
||||
16.
17.
18.
№ 7.
1)
;
2)
;
3)
;
1) |
|
|
|
|
2) |
|
|
3) |
|
|
|
19 |
54±0,5 |
38,235±0,001 |
3,14 |
|
19 |
36,5±0,1 |
26,35±0.005 |
19 |
2,436 |
0,15 |
1,27 |
20 |
72±0, |
3,274±0,002 |
3,14 |
|
20 |
41,4±0,2 |
31,75±0,003 |
20 |
7,834 |
0,21 |
3,71 |
21 |
31,0±0,01 |
7,345±0,001 |
3,14 |
|
21 |
52,6±0,01 |
48,36±0.001 |
21 |
4,539 |
0,34 |
5,93 |
19.
20.
21.
№ 8.
1)
;
2)
;
3)
;
1) |
22 |
23 |
24 |
|
3) |
22 |
23 |
24 |
|
1,6531±0,0003 |
2,348±0,002 |
3,804±0,003 |
|
|
28,3 |
17,2 |
48,3 |
|
3,78±0,002 |
4,37±0,004 |
4,05±0,003 |
|
|
42,08 |
9,344 |
32,14 |
|
0,158±0,0005 |
0,235±0,0003 |
0,318±0,0002 |
|
|
84,2 |
76 |
45 |
2) |
|
|
|
|
|
22. |
9,542±0,001 |
3,128±0,002 |
2,8±0,03 |
0,172±0,001 |
5,4±0,02 |
23. |
8,357±0,003 |
2,48±0,004 |
3,17±0,01 |
1,315±0,0004 |
2,4±0,02 |
24. |
4,218±0,001 |
1,57±0,006 |
2,32±0,02 |
2,418±0,004 |
1,8±0,01 |
22.
23.
24.
№ 9.
1)
;
2)
;
3)
;
1) |
25. |
26. |
27. |
|
3) |
25. |
26. |
27. |
|
0,7568±0,0002 |
0,8345±0,0004 |
0,6384±0,0002 |
|
|
46,3 |
10,5 |
2,48 |
|
21,7±0,02 |
13,8±0,03 |
32,7±0,04 |
|
|
29,72 |
34,18 |
5,344 |
|
2,65±0,01 |
1,84±0,006 |
4,88±0,03 |
|
|
37,654 |
27,327 |
6,0218 |
2) |
|
|
|
|
25. |
10,82±0,03 |
2,786±0,0006 |
0,28±0,006 |
14,7±0,06 |
26. |
9,37±0,004 |
3,108±0,0003 |
0,46±0,002 |
15,2±0,04 |
27. |
11,45±0,01 |
4,431±0,002 |
0,75±0,003 |
16,7±0,05 |
25.
26.
27.
№ 10.
1)
;
2)
;
3)
;
1) |
28. |
29. |
30. |
|
2) |
28. |
29. |
30. |
|
54,8±0,02 |
38,5±0,01 |
17,3±0,03 |
|
|
2,0435±0,0001 |
1,175±0,002 |
4,456±0,01 |
|
2,45±0,01 |
3,35±0,02 |
5,73±0,01 |
|
|
4,2±0,05 |
5,8±0,01 |
6,344±0,02 |
|
0,863±0,004 |
0,734±0,001 |
0,956±0,004 |
|
|
0,82±0,01 |
0,65±0,02 |
0,42±0,03 |
3) |
|
|
|
|
4) |
28. |
29. |
28. |
5,27 |
0,0562 |
158,35 |
61,21 |
|
|
|
29. |
7,31 |
0,0761 |
234,36 |
81,26 |
|
30.
|
|
30. |
3,28 |
0,0545 |
341,17 |
52,34 |
|
||
