Решение нестационарных задач математической физики

Операционный метод может быть применён для решения нестационарных задач математической физики. Рассмотрим случай, когда искомая функция зависит лишь от пространственной координаты x и времени t.

Для уравнения теплопроводности будем решать I краевую задачу:

,

, ¾ начальные условия и , ¾ краевые условия.

Пусть все функции являются оригиналами.

Обозначим ¾ изображение по Лапласу:

Тогда,

,

,

Тогда краевые условия:

Уравнение в изображениях:

Пример 154. Концы струны , закреплены жестко. Начальные отклонения заданы равенством:

Начальные скорости равны нулю. Найти отклонения при .

Решение. Процесс описывается волновым уравнением:

Дано:

В изображениях:

,

Решение этого уравнения:

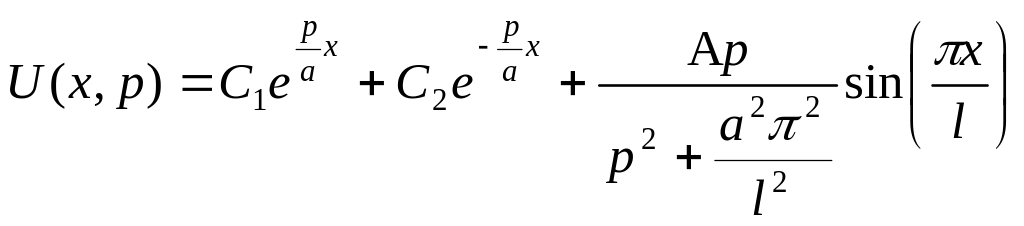
или с учетом краевых условий:

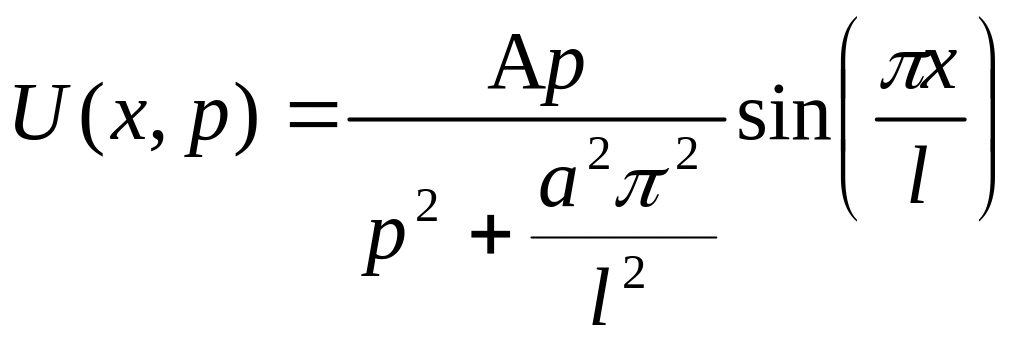
— синусоида по с амплитудой, зависящей от времени .

Пример 155. Найти решение уравнения теплопроводности:

,

удовлетворяющее начальным и граничным условиям:

Решение. Запишем операторное уравнение:

Общее решение этого дифференциального уравнения есть:

Так как функции и при является ограниченной, то . Используя граничные условия: , находим: .

Тогда: .

Имеется формула: ,

тогда

156. Решить краевую задачу

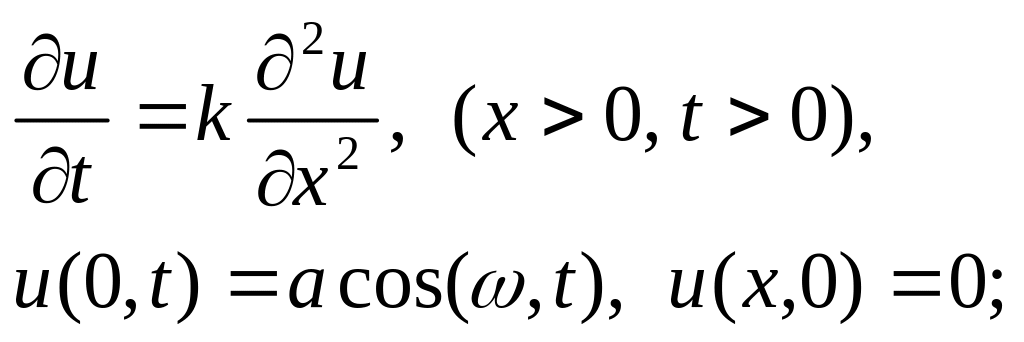
ответ:

Индивидуальные задания по теме «Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами операционным методом»

Решить дифференциальные уравнения с начальными условиями:

1. 1. ,

   2. ,

   3. , .

2. 1. ,

   2. , .

   3. , .

3. 1. , .

   2. , .

   3. , .

4. 1. , .

   2. , .

   3. , .

5. 1. , .

   2. , .

   3. , .

6. 1. , .

   2. , .

   3. , .

7. 1. , .

   2. , .

   3. , .

8. 1. , .

   2. , .

   3. , .

9. 1. , .

   2. , .

   3. , .

10. 1. , .

    2. , .

    3. , .

11. 1. , .

    2. , .

    3. , .

12. 1. , .

    2. , .

    3. , .

13. 1. , .

    2. , .

    3. , .

14. 1. , .

    2. , .

    3. , .

15. 1. , .

    2. , .

    3. , .

16. 1. , .

    2. , .

    3. , .

17. 1. , .

    2. , .

    3. , .

18. 1. , .

    2. , .

    3. , .

19. 1. , .

    2. , .

    3. , .

20. 1. , .

    2. , .

    3. , .

21. 1. , .

    2. , .

    3. , .

22. 1. , .

    2. , .

    3. ,

23. 1. , .

    2. , .

    3. , .

24. 1. , .

    2. , .

    3. , .

25. 1. , .

    2. , .

    3. , .

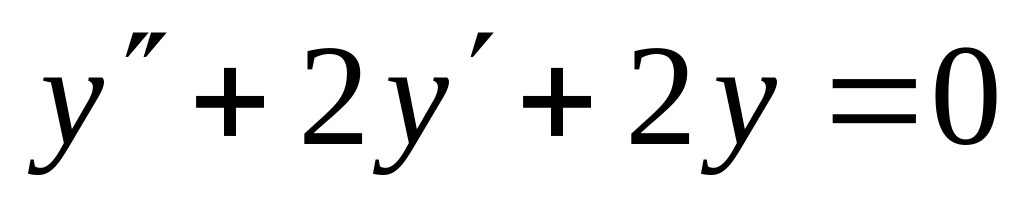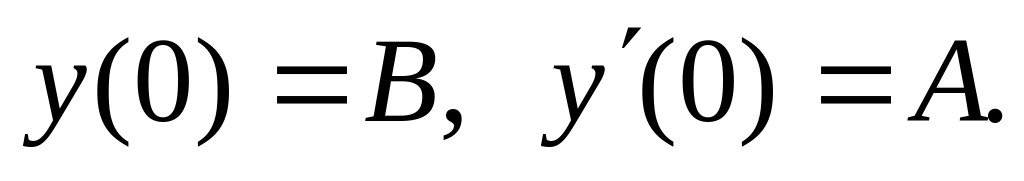
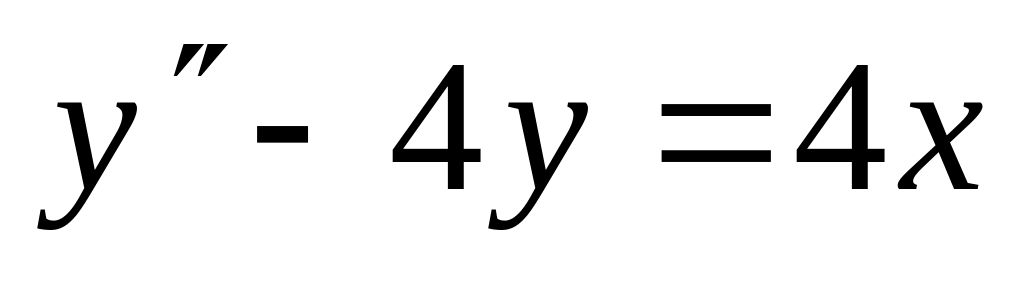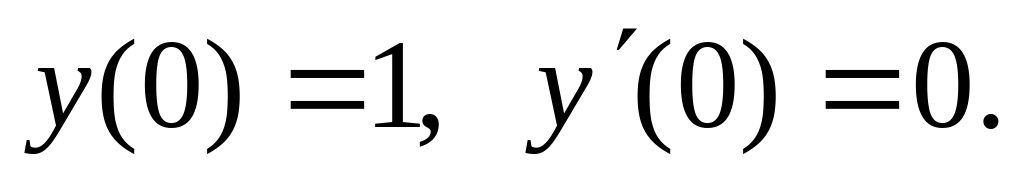
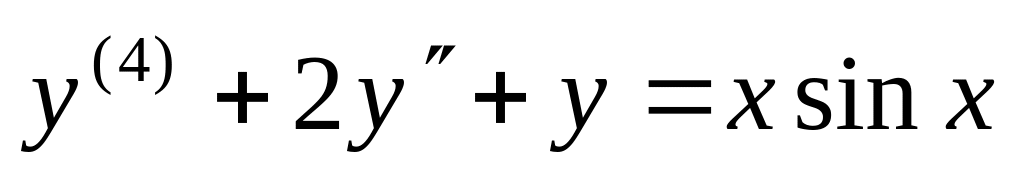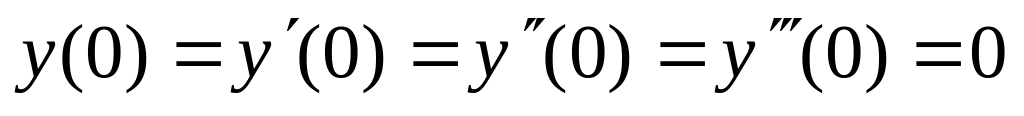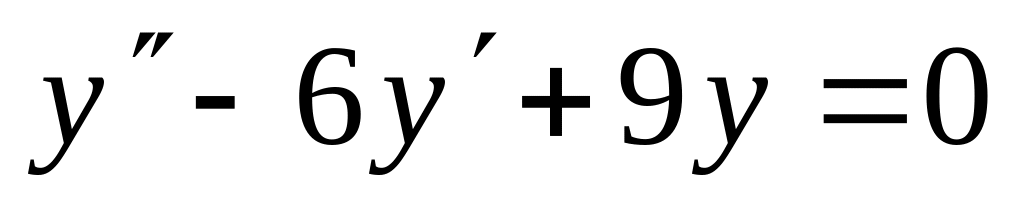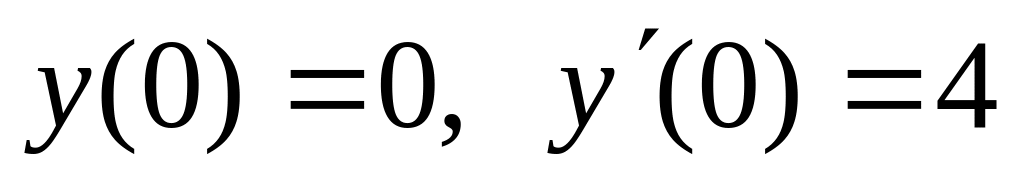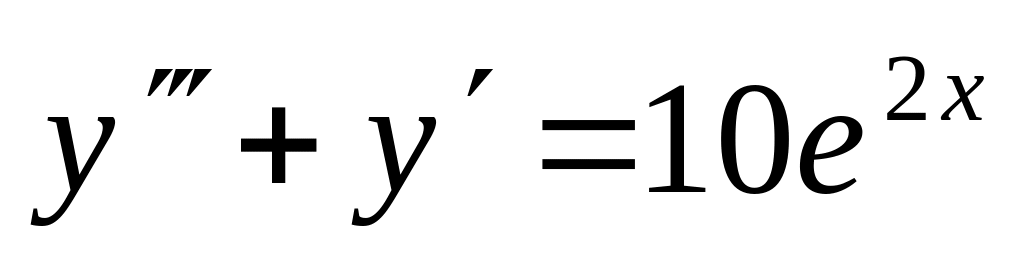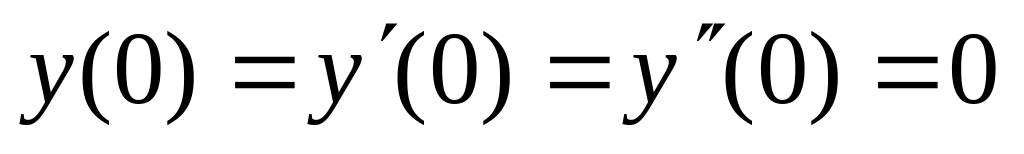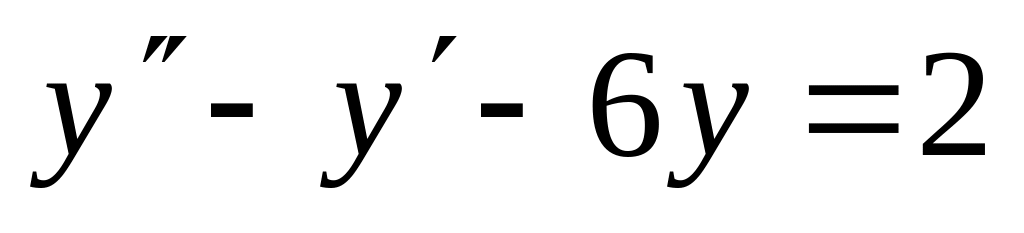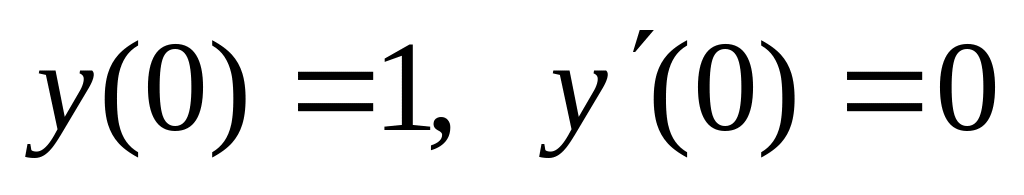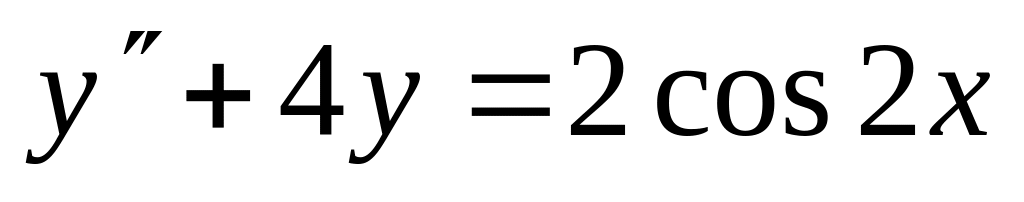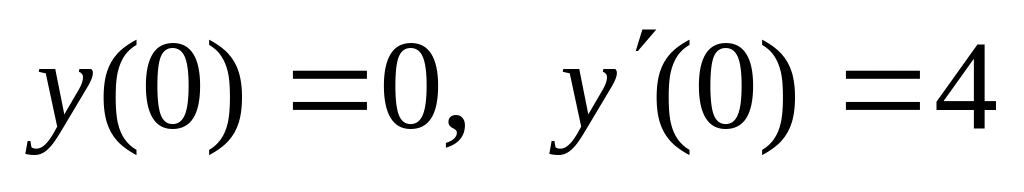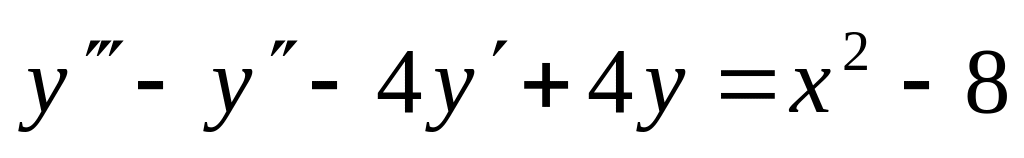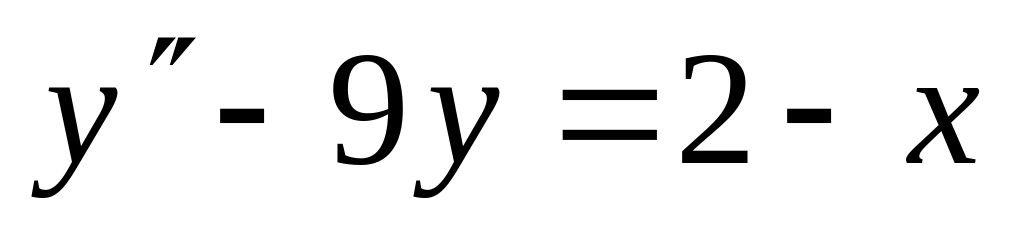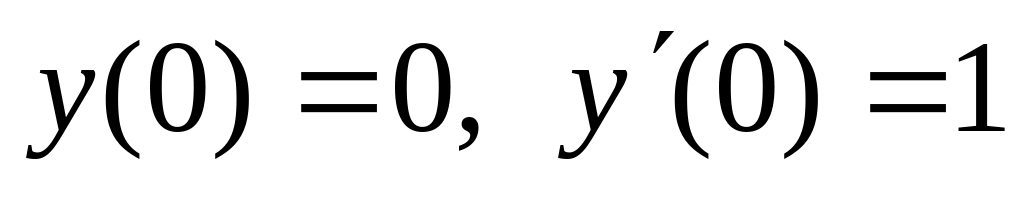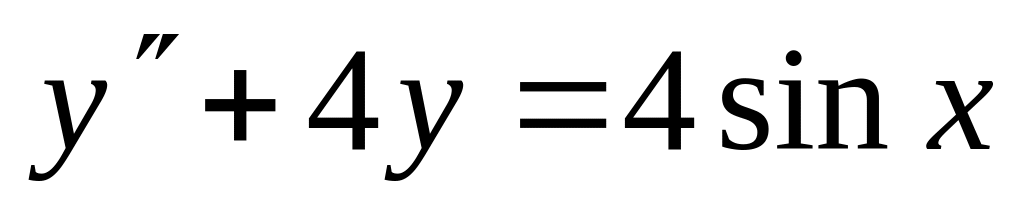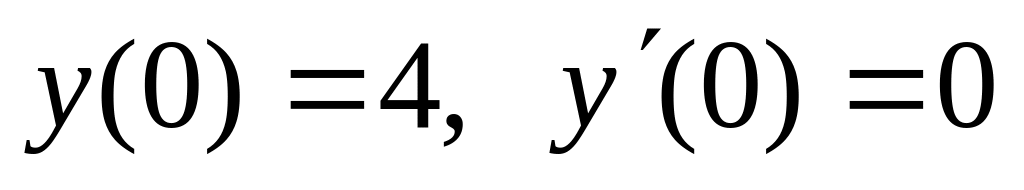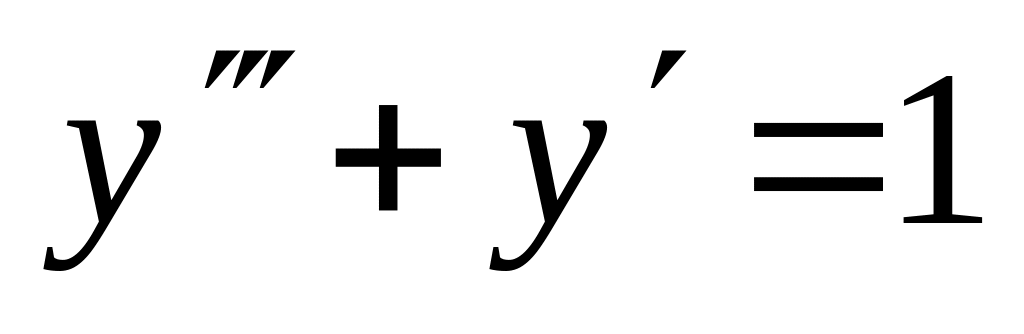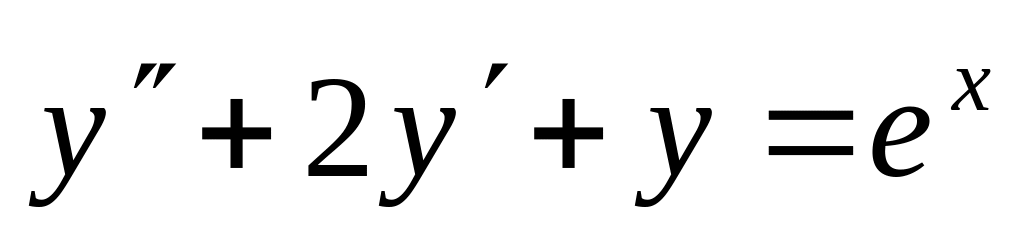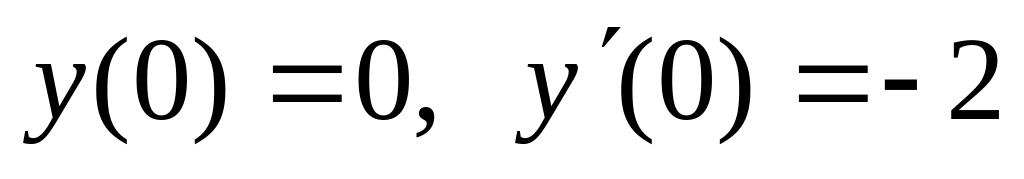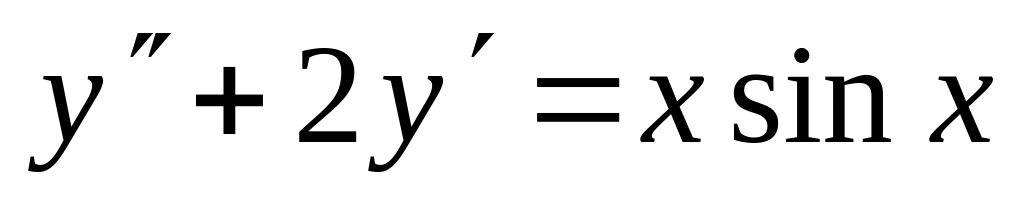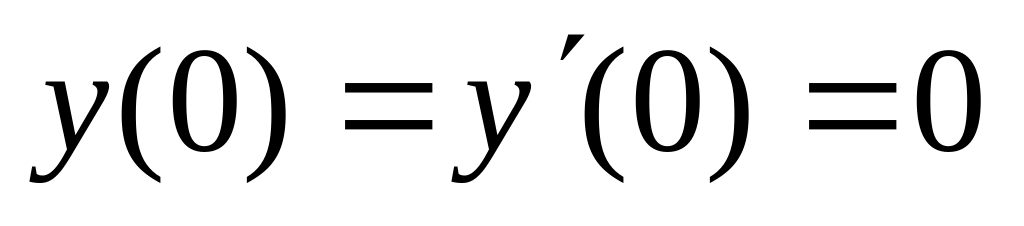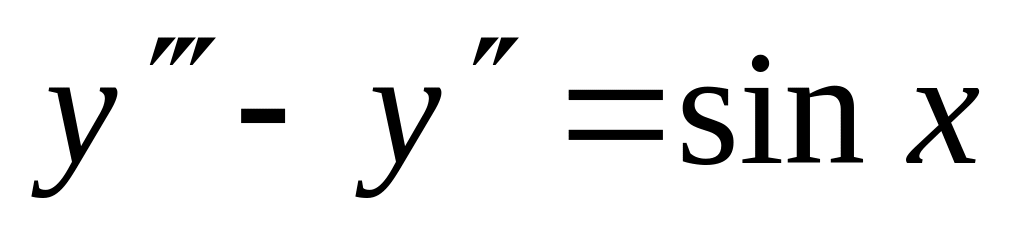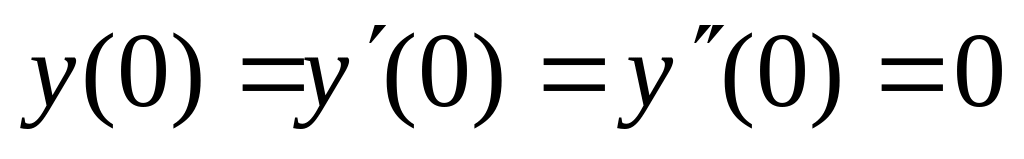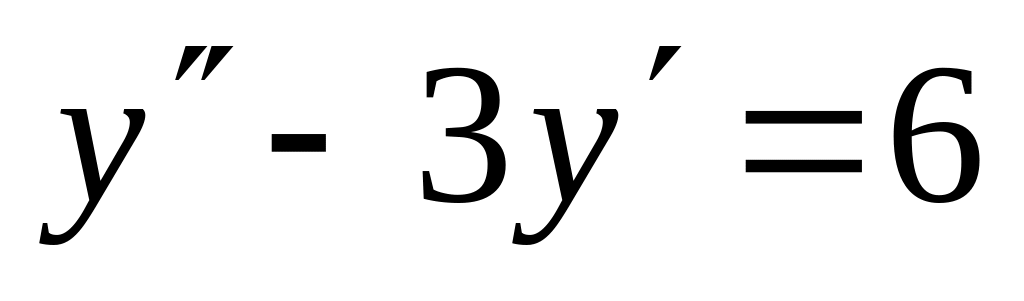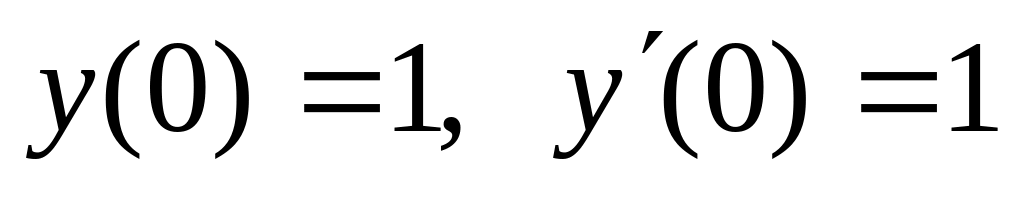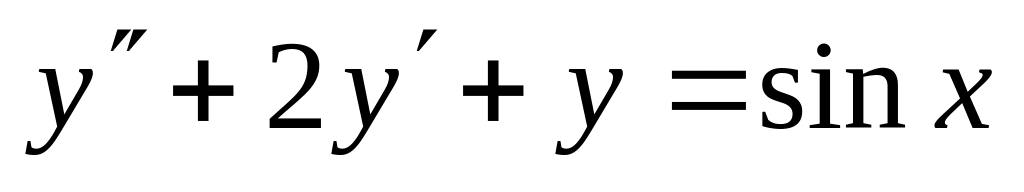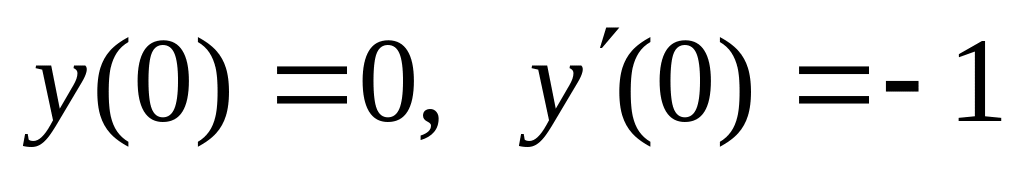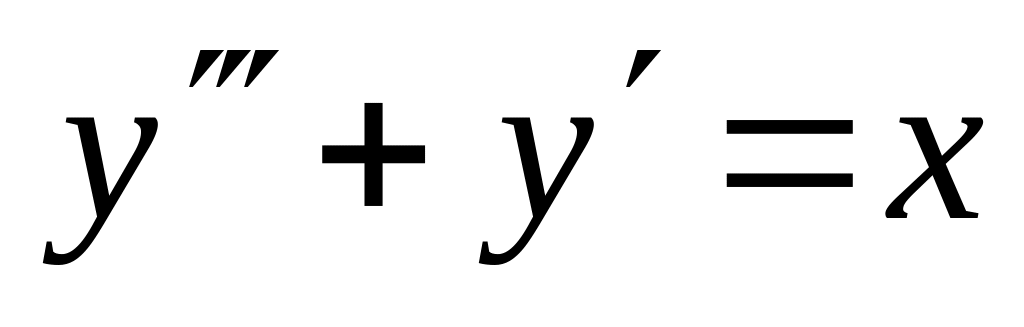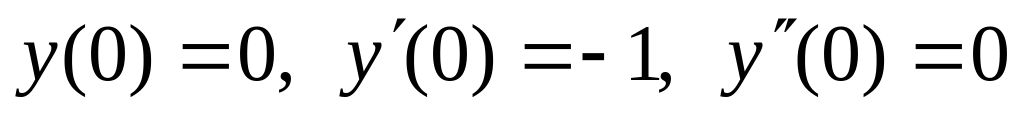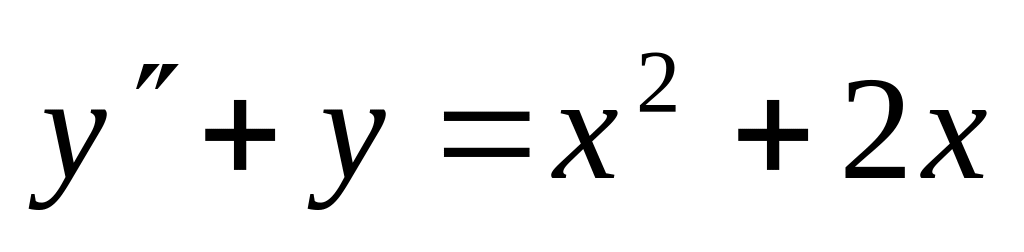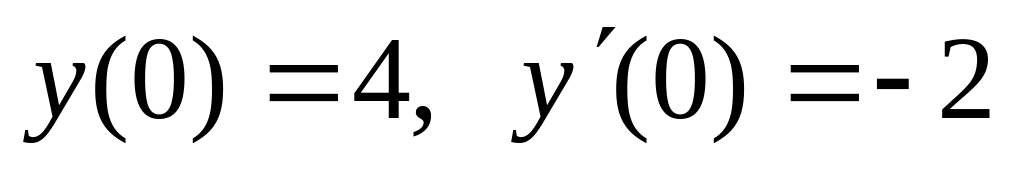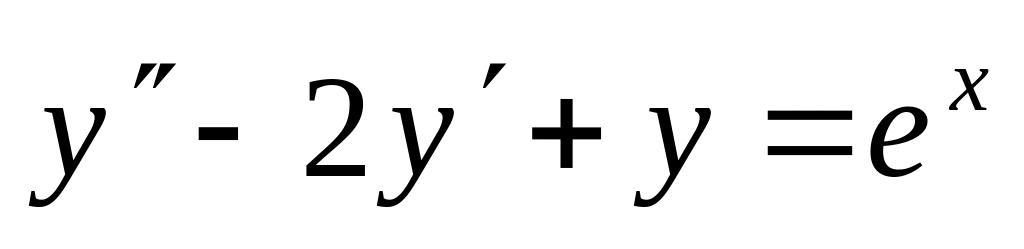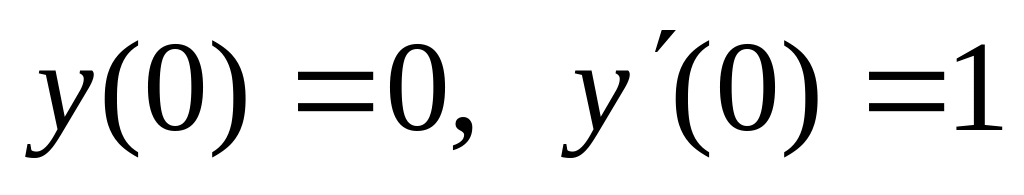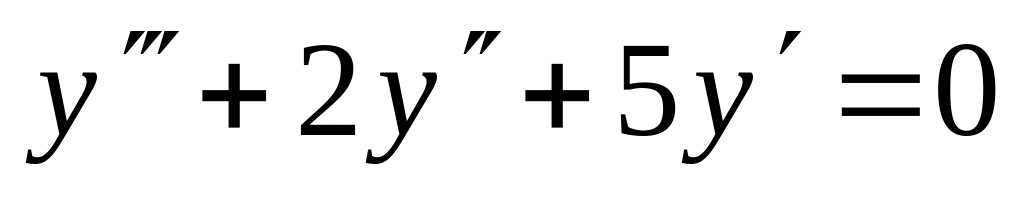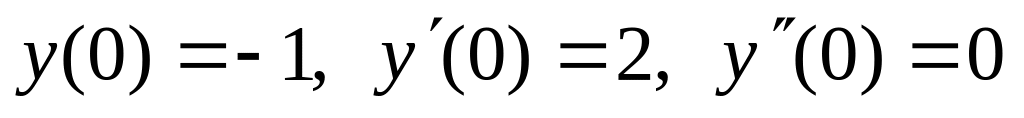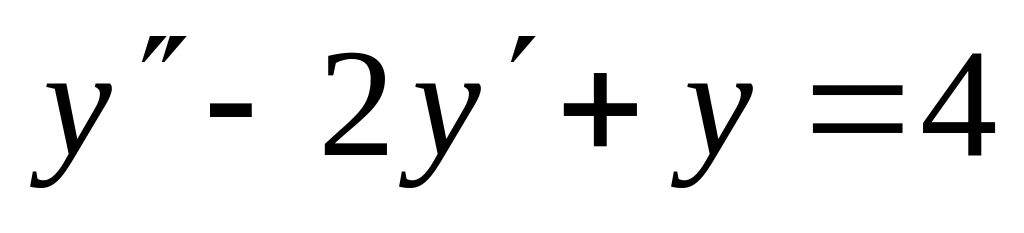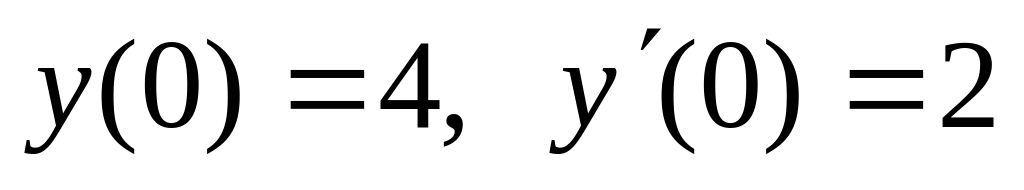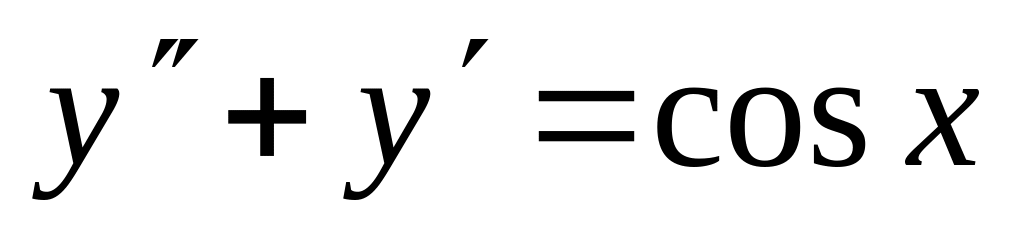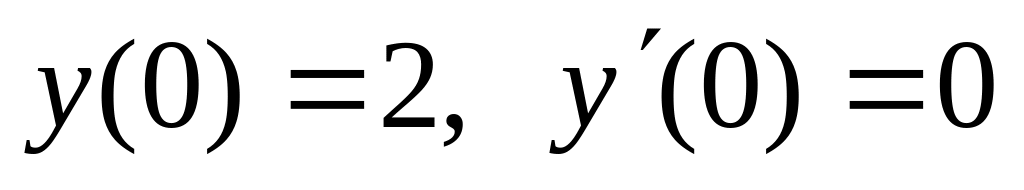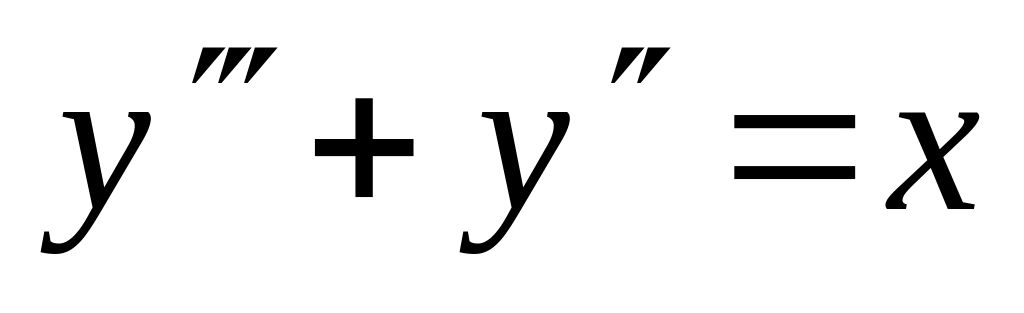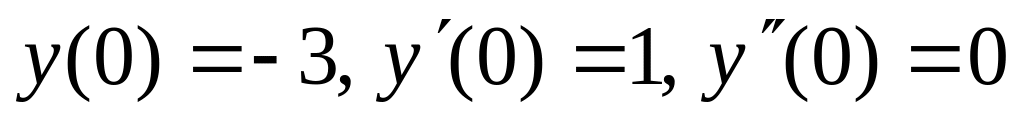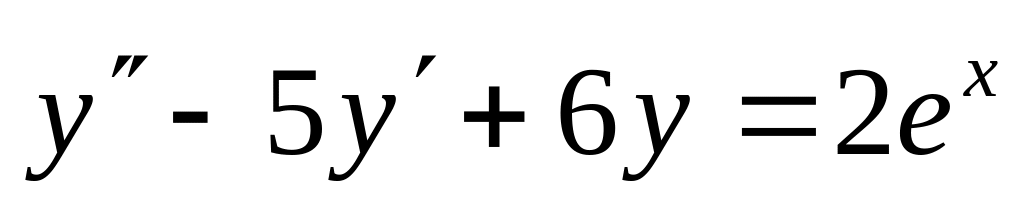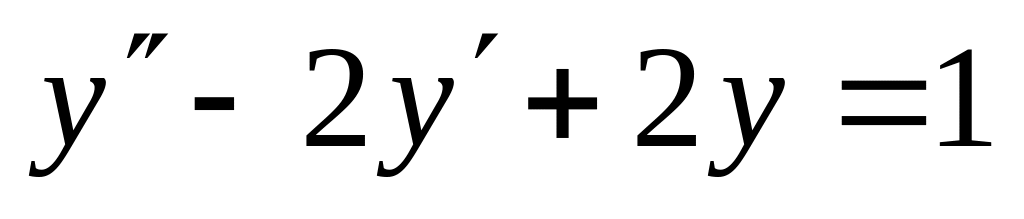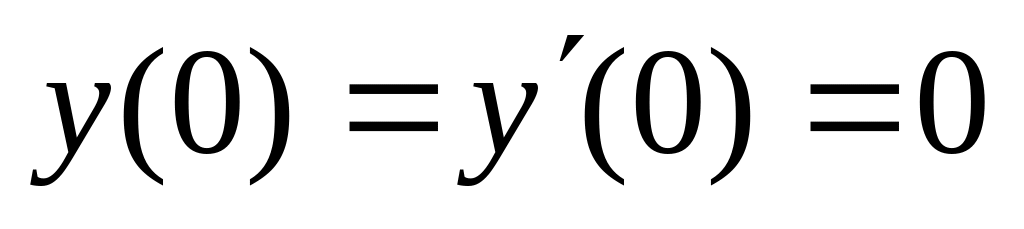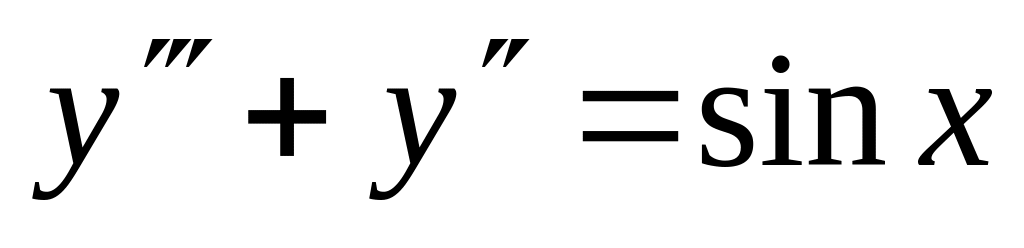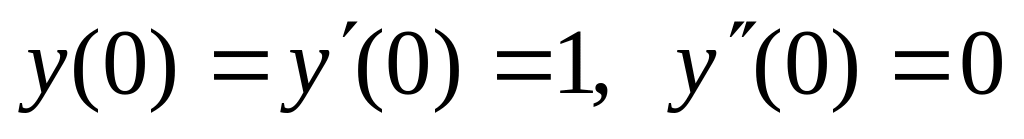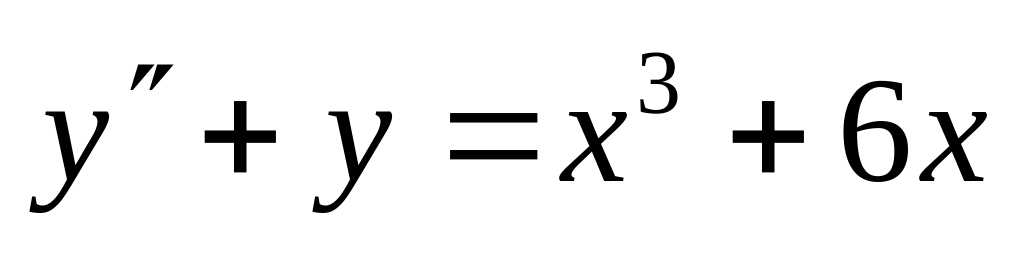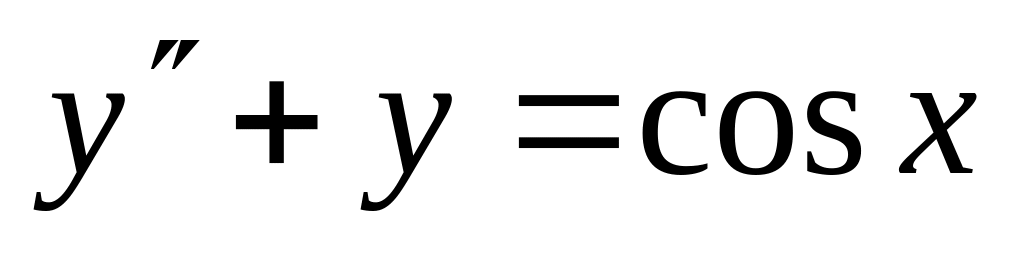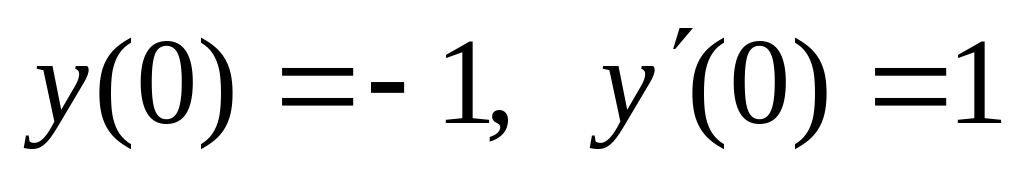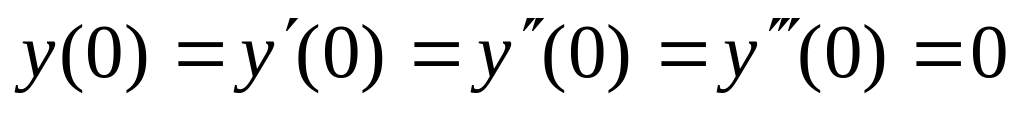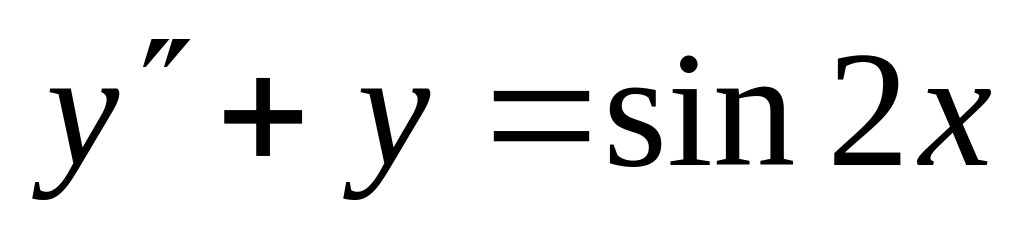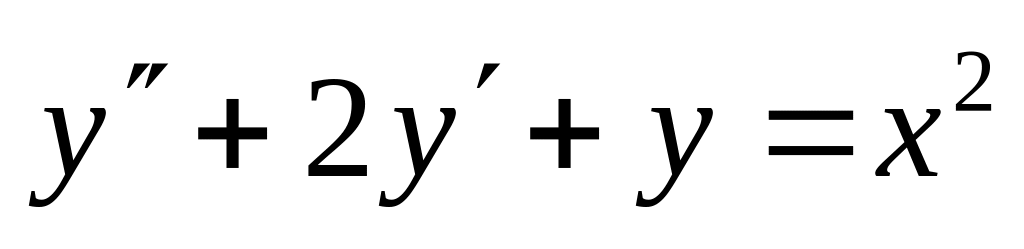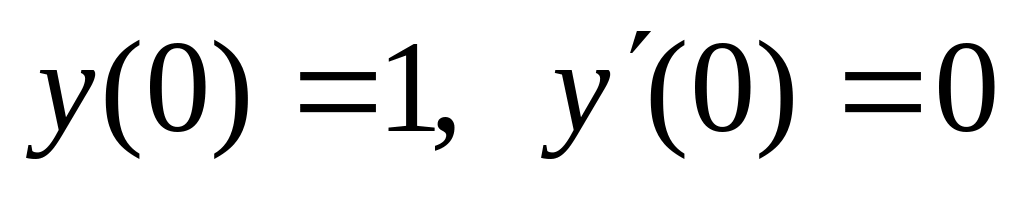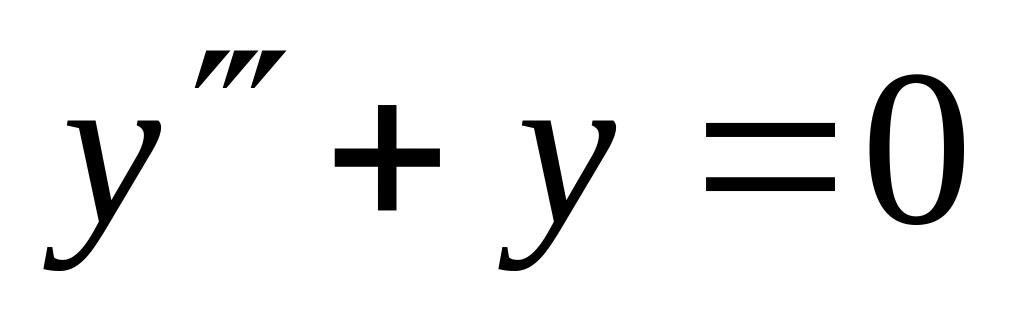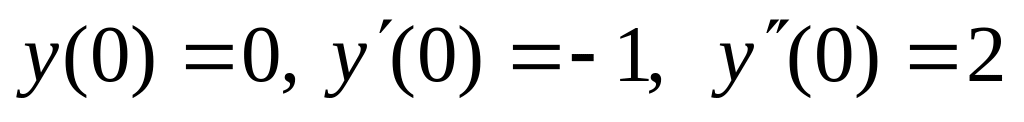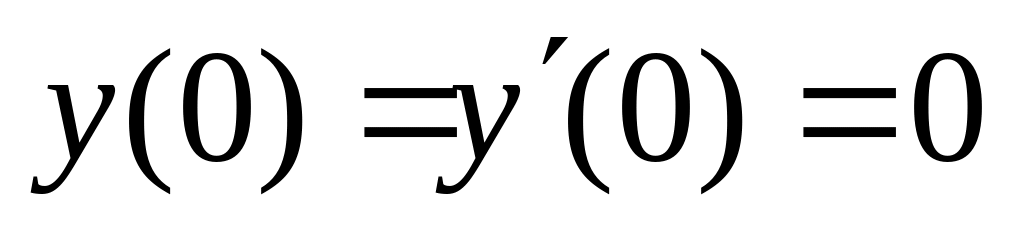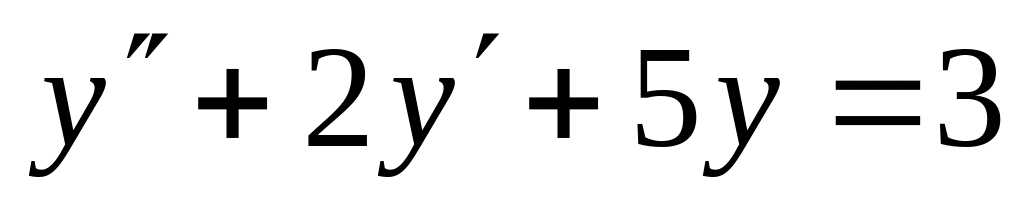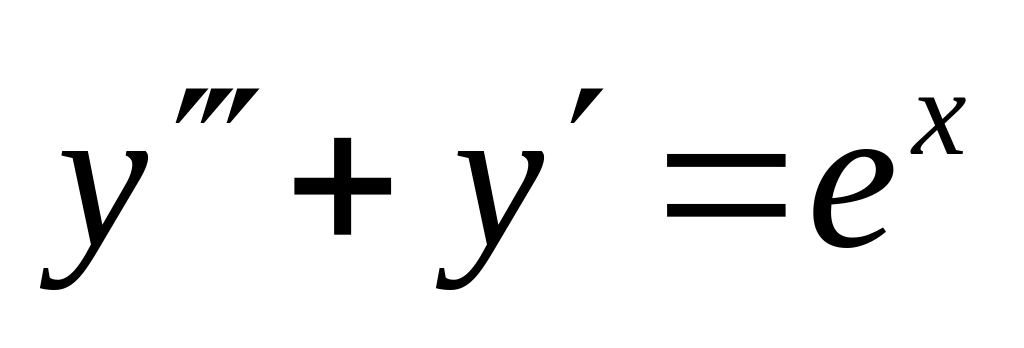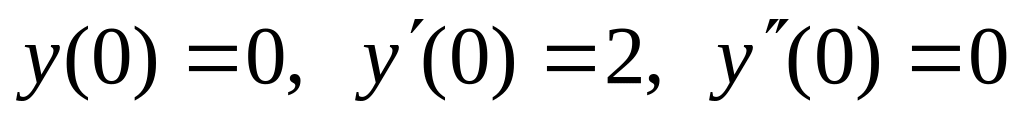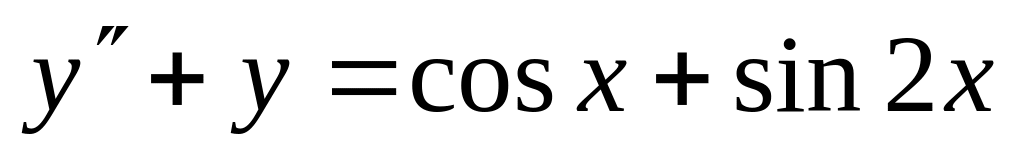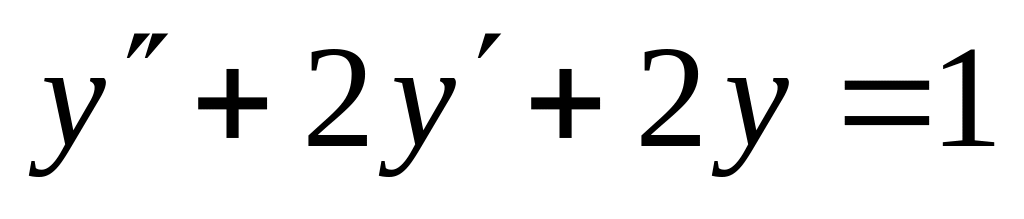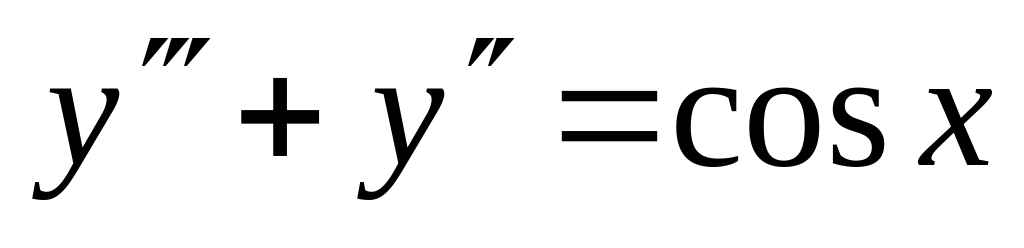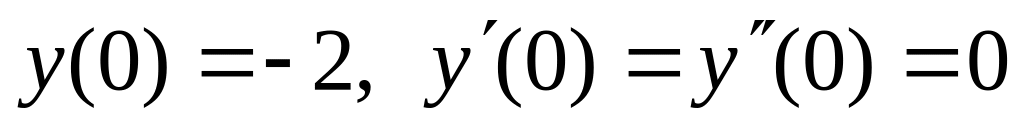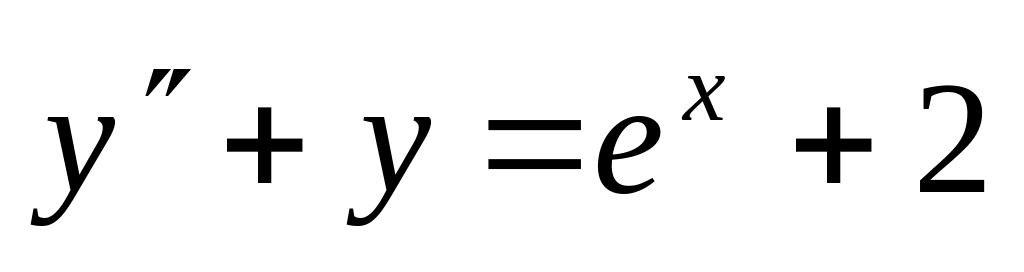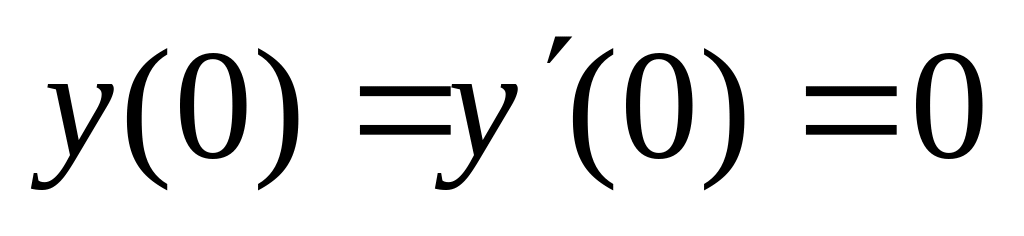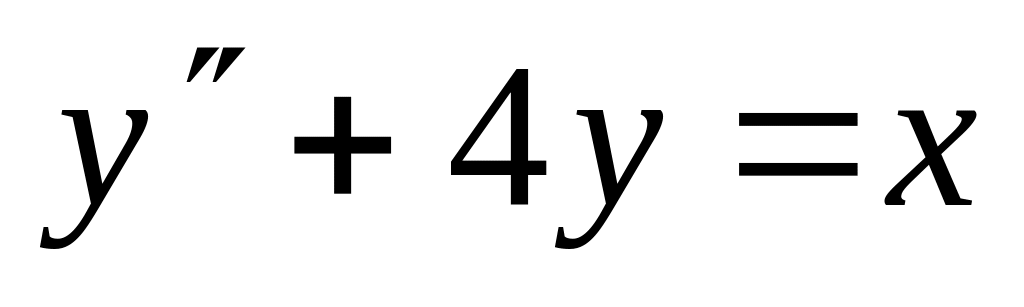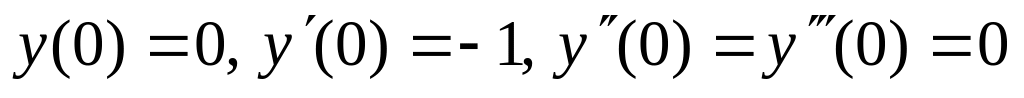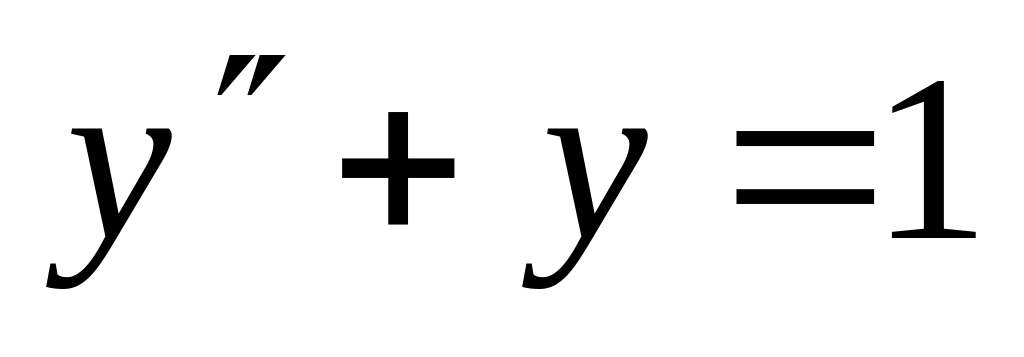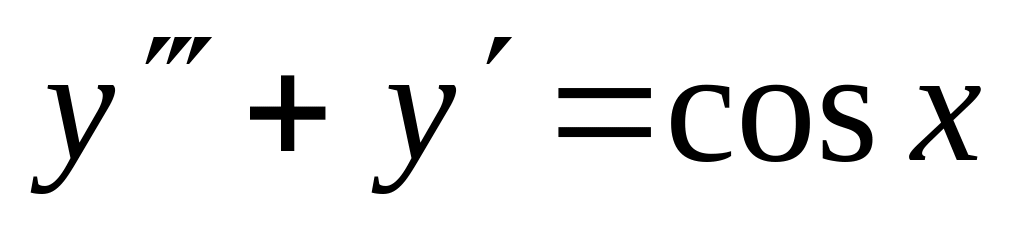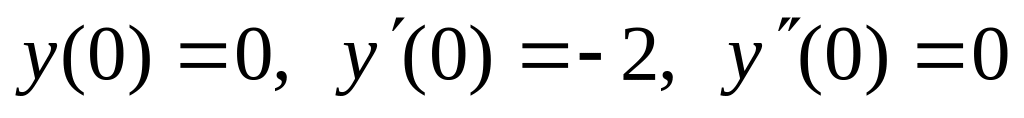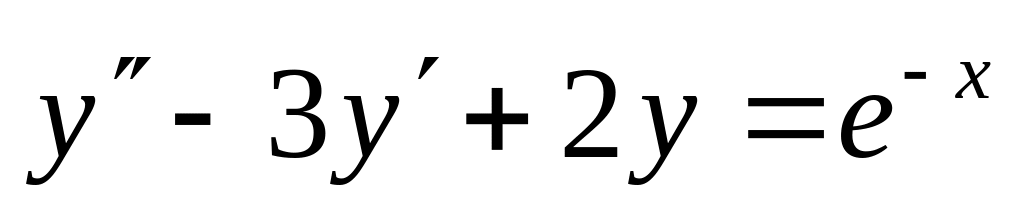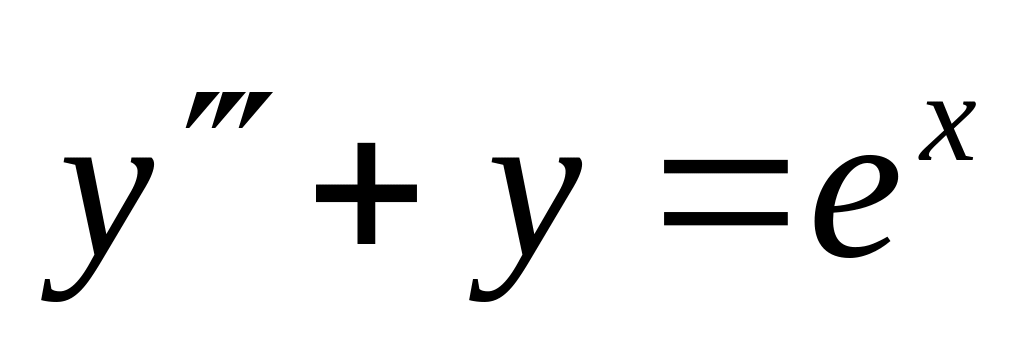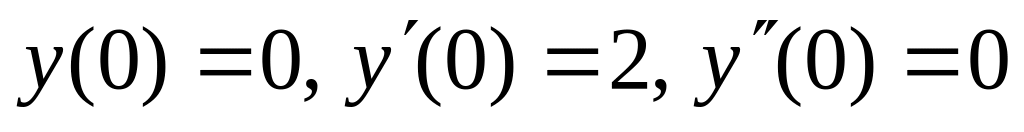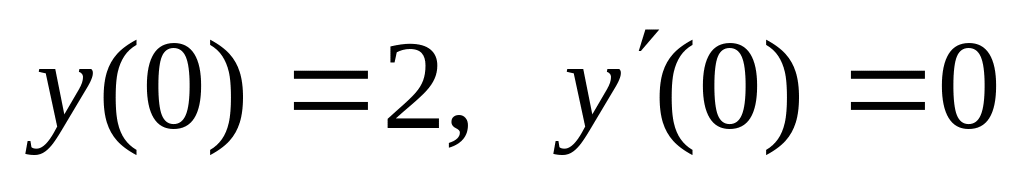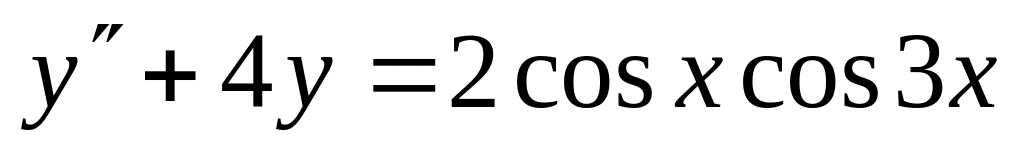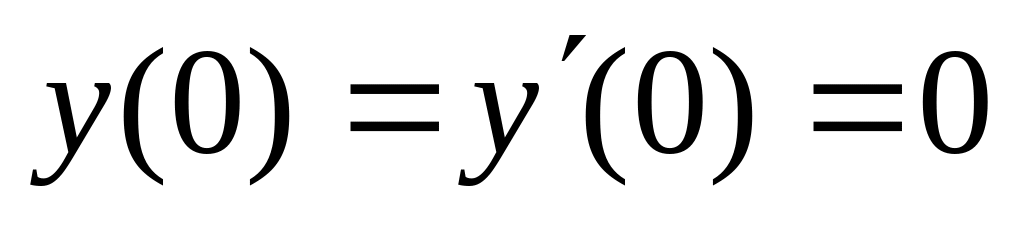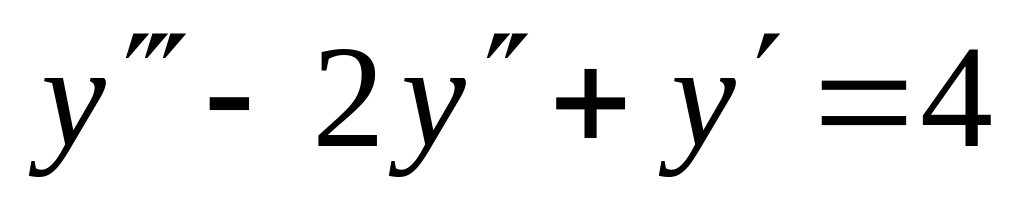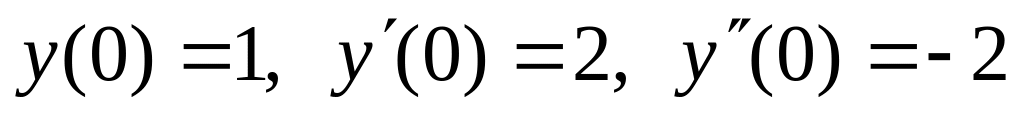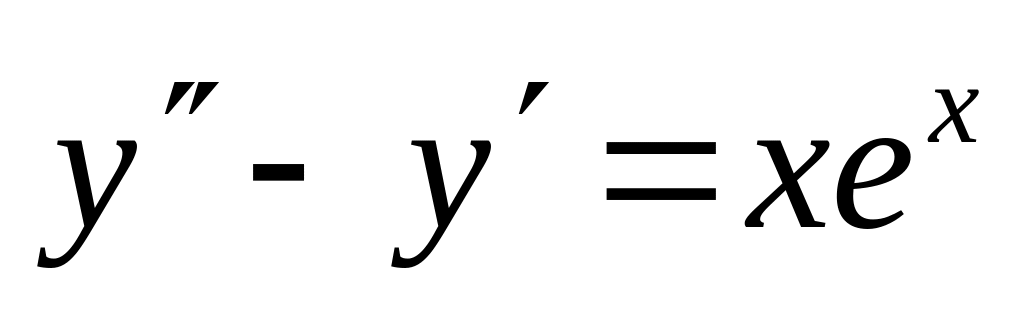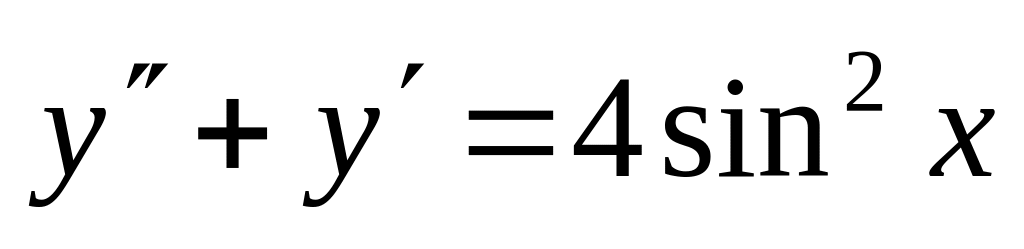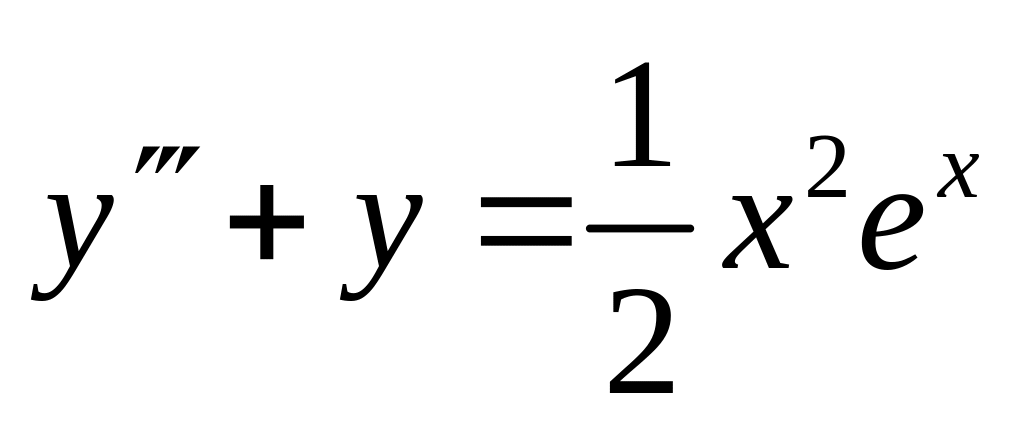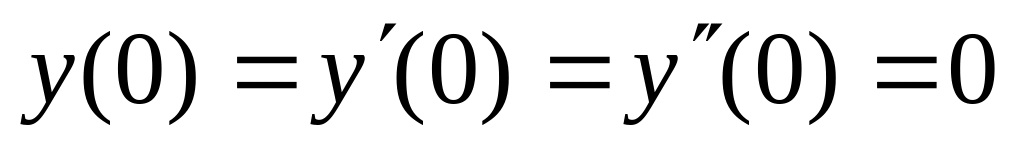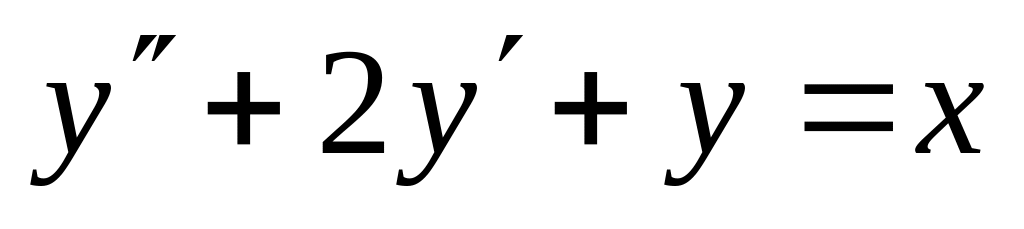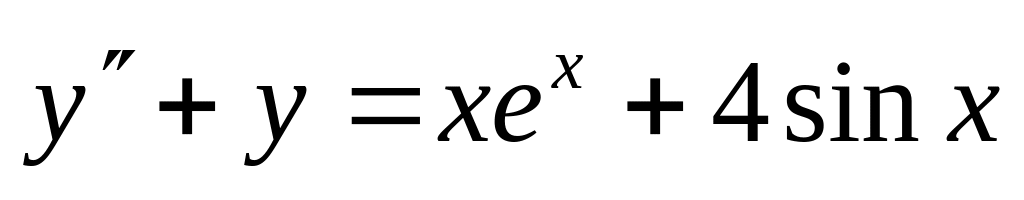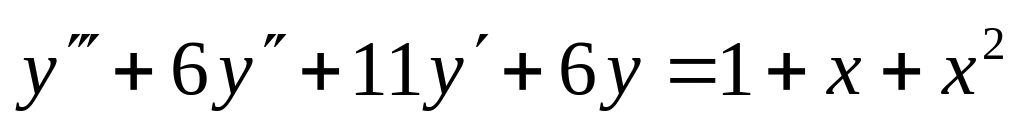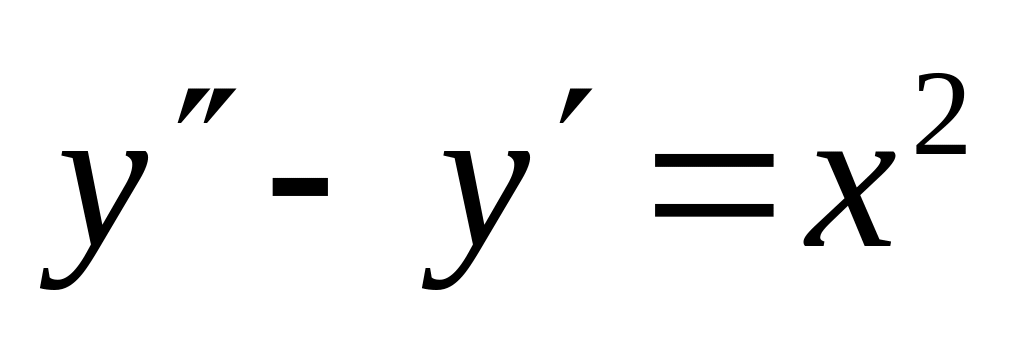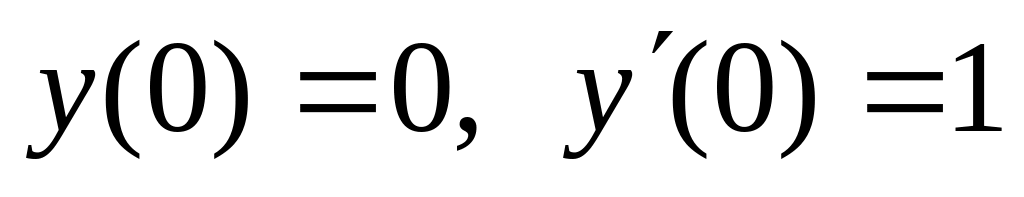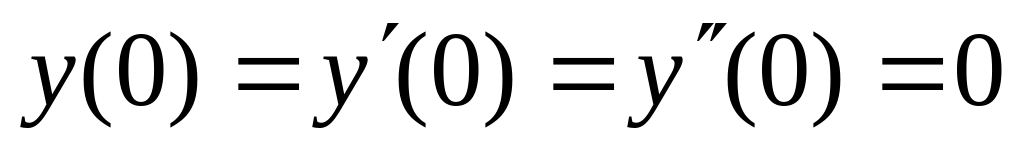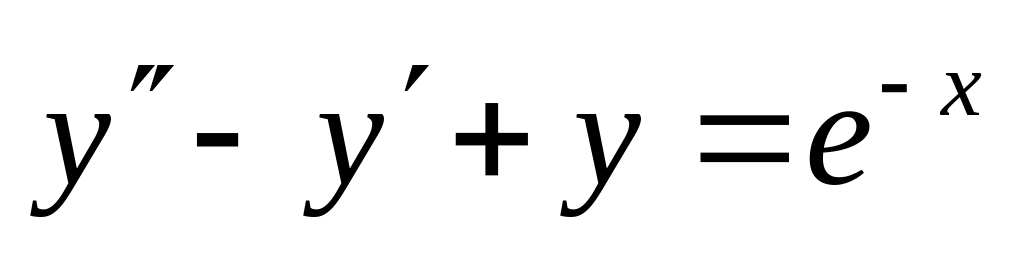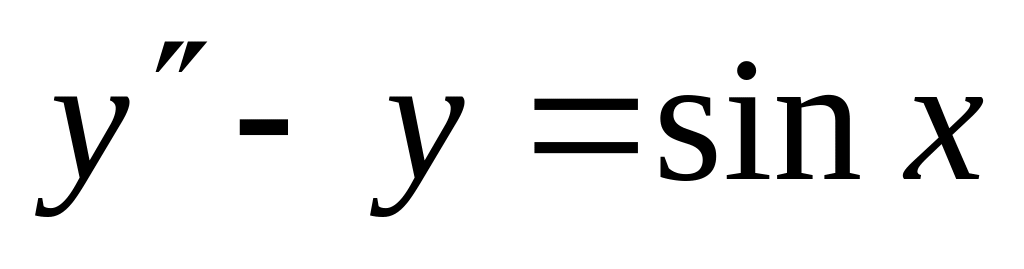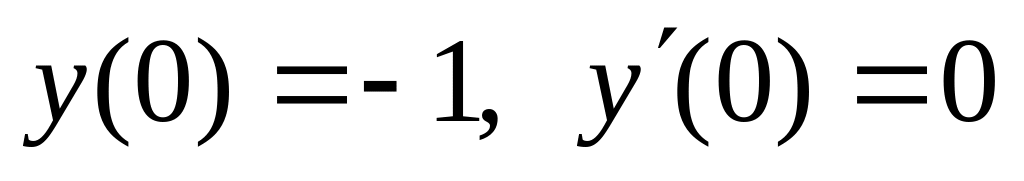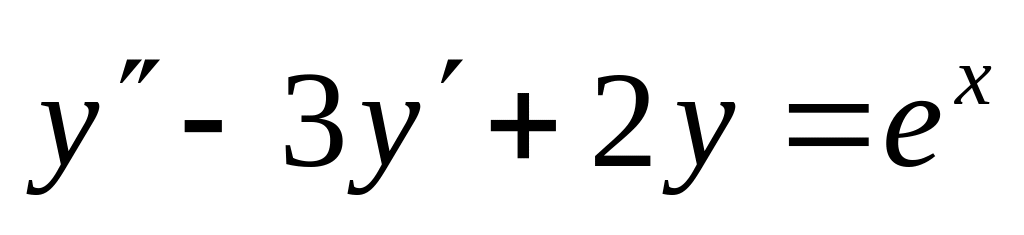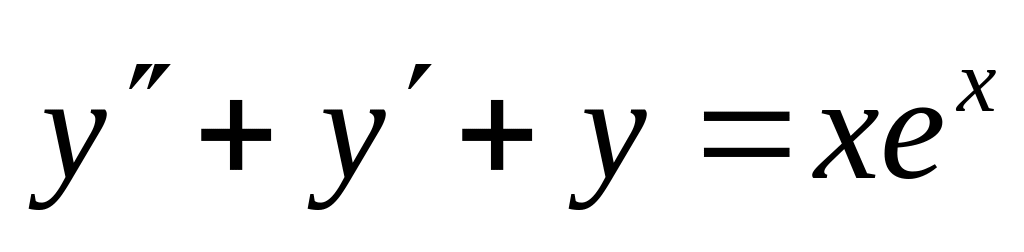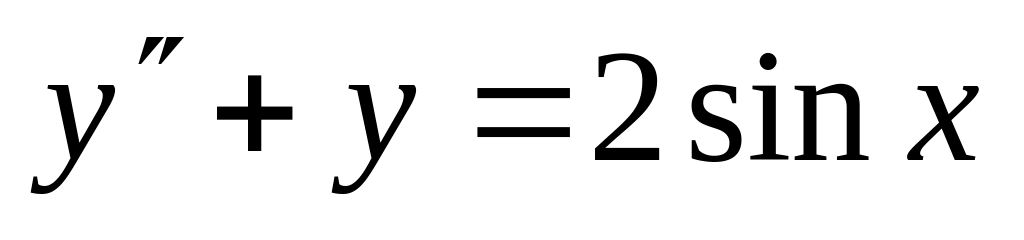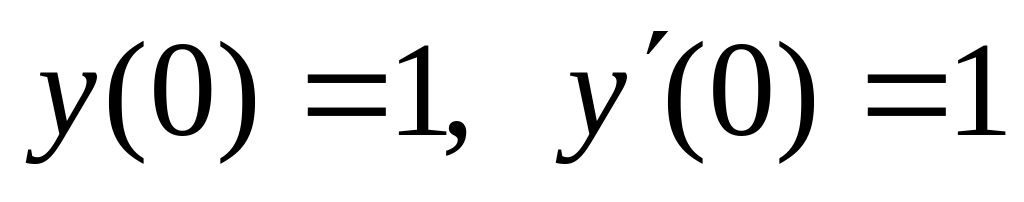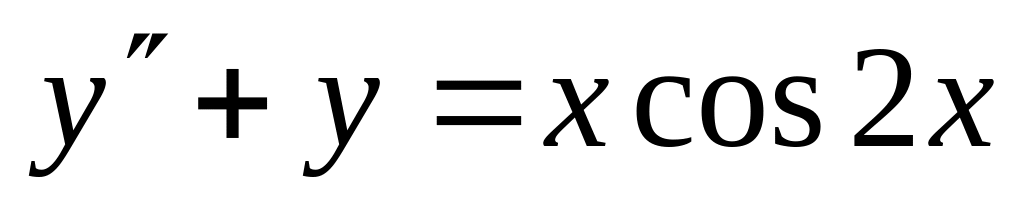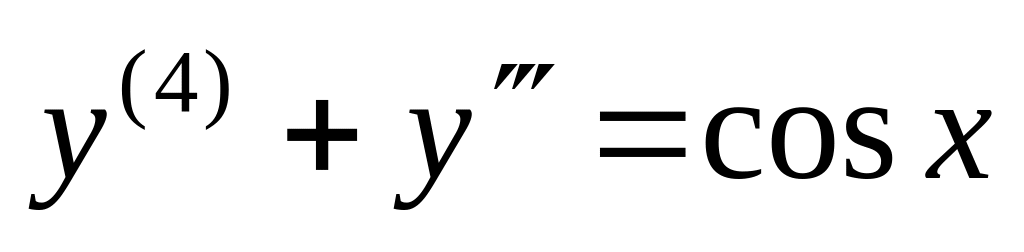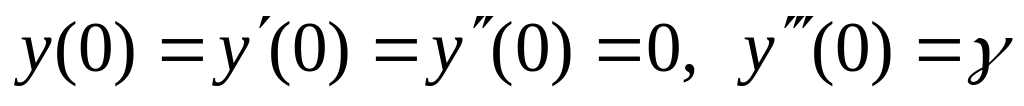
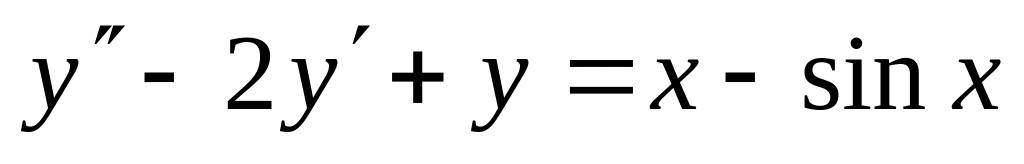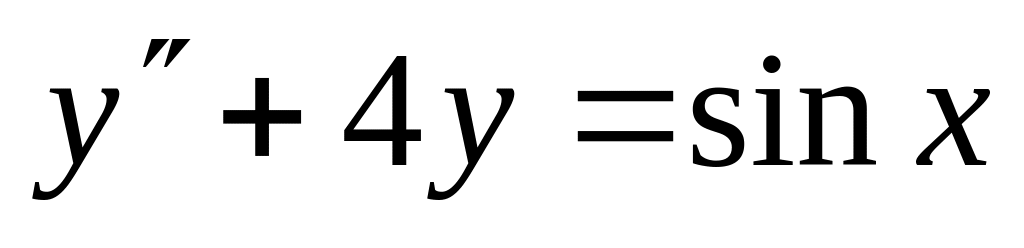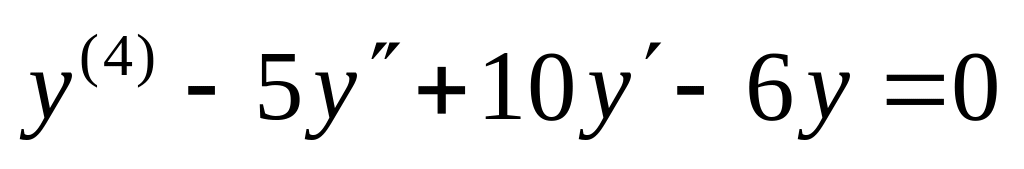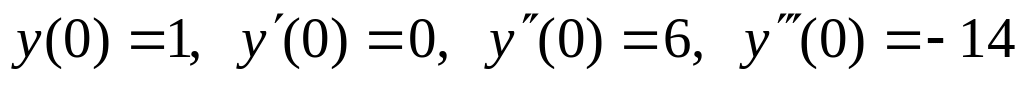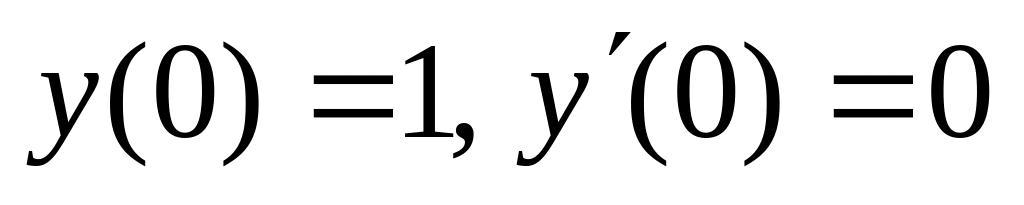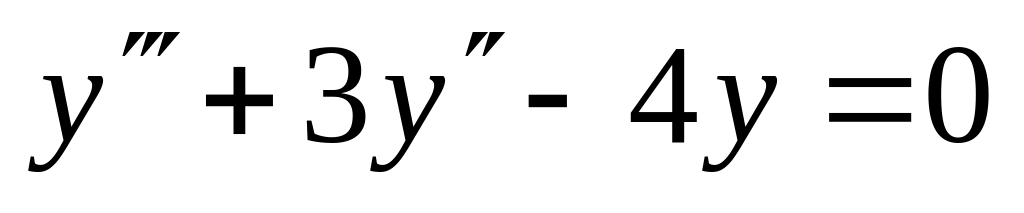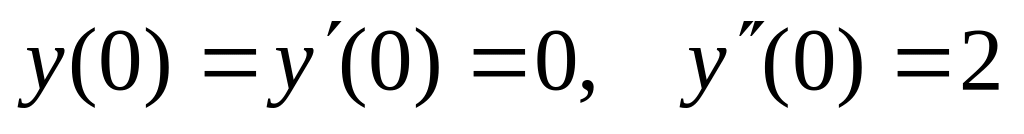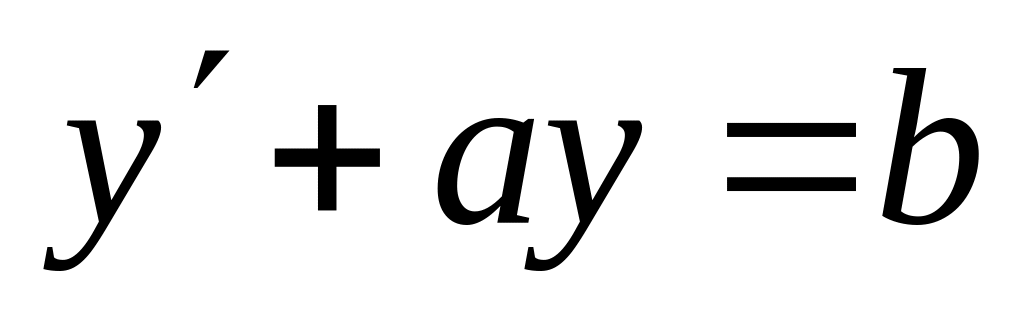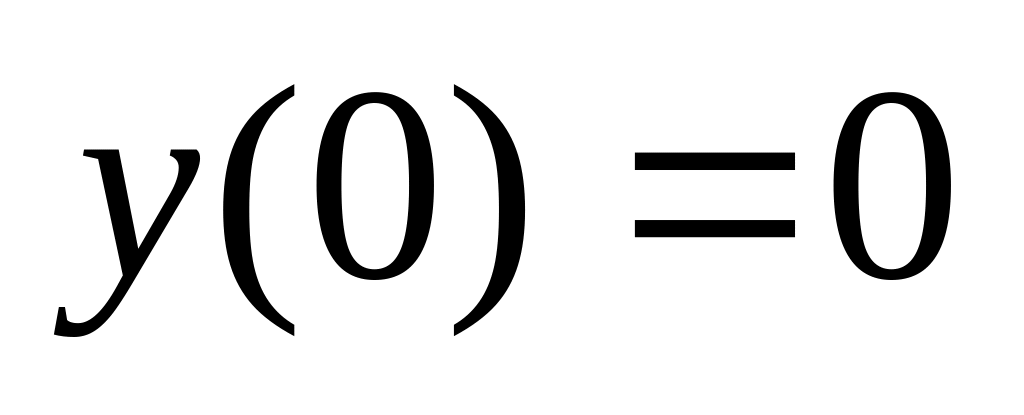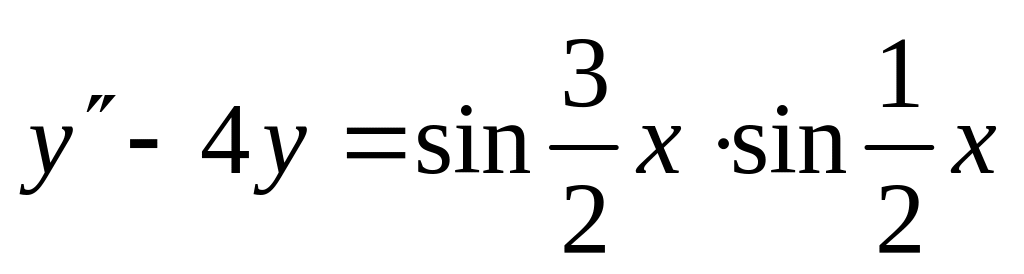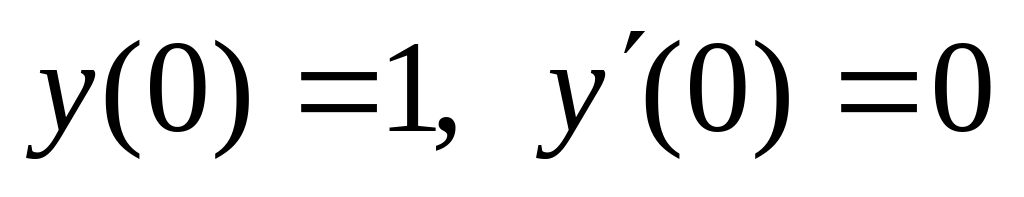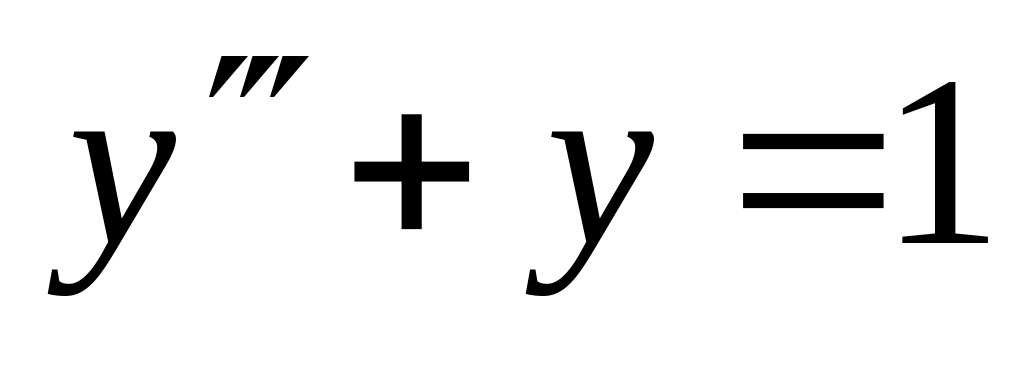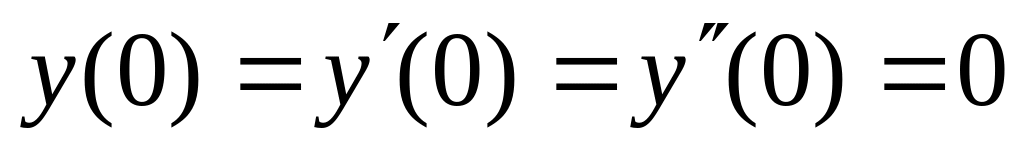Ответы для индивидуальных заданий по теме «Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами операционным методом»

1. 1. .

   2. .

   3. .

2. 1. .

   2. .

   3. .

1. .

2. .

3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. 

   2. .

   3. 

3. .

   1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

4. .

5. .

6. .

3. 1. .

   2. .

   3. 

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. 

.

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

3. 1. .

   2. .

   3. .

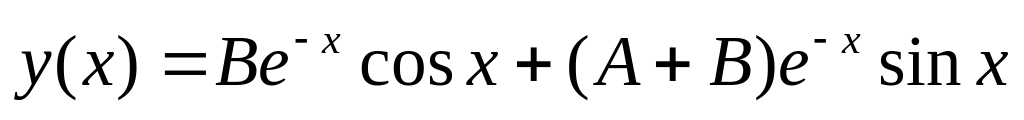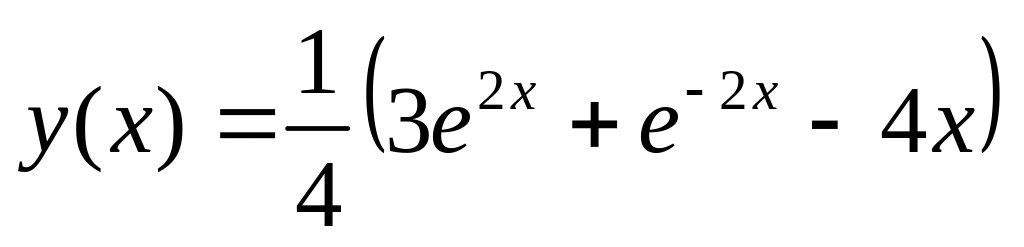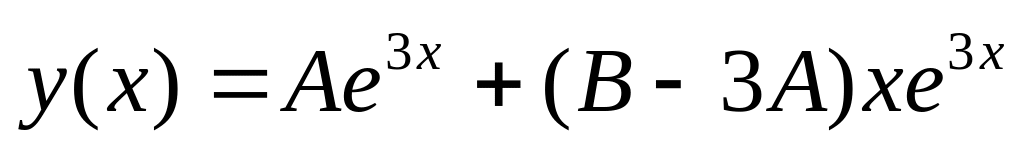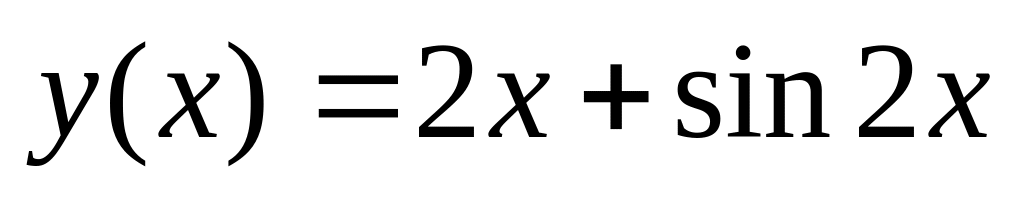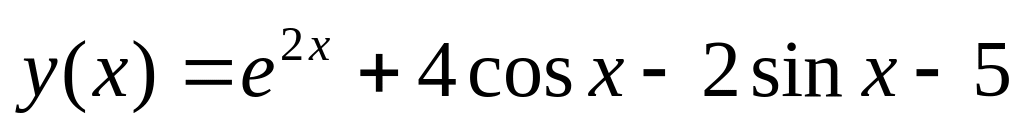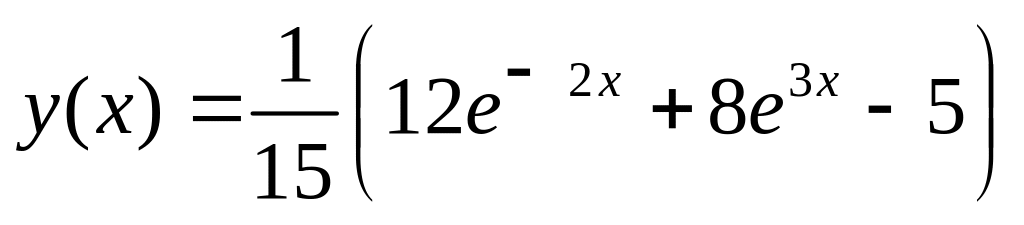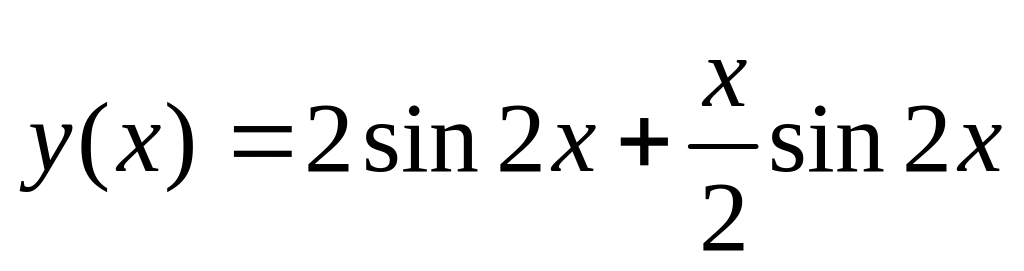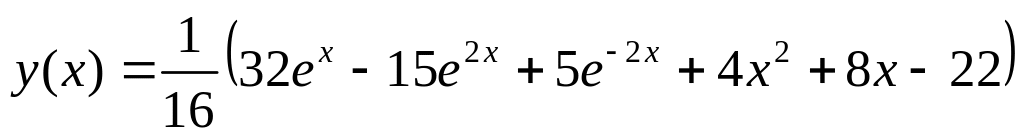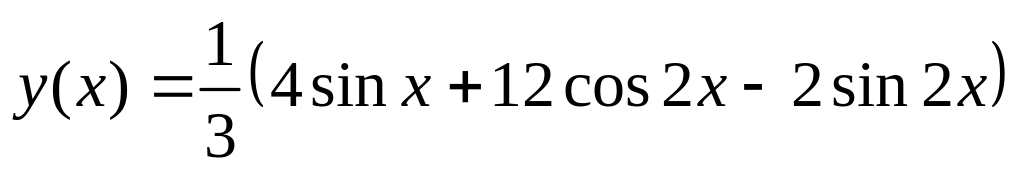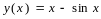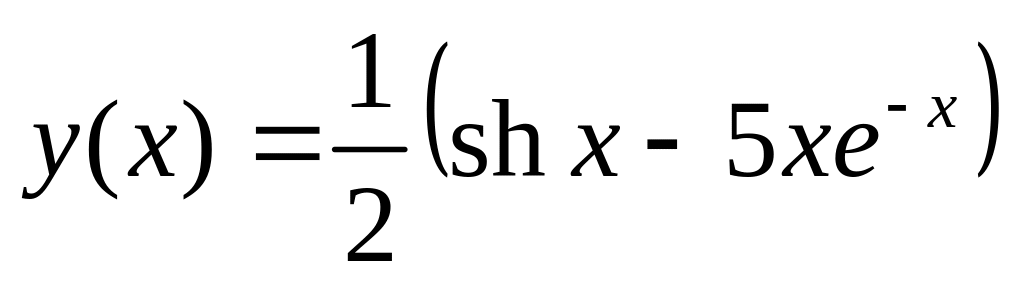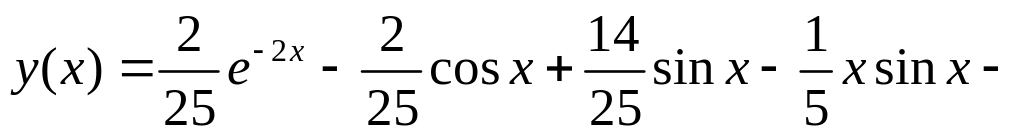
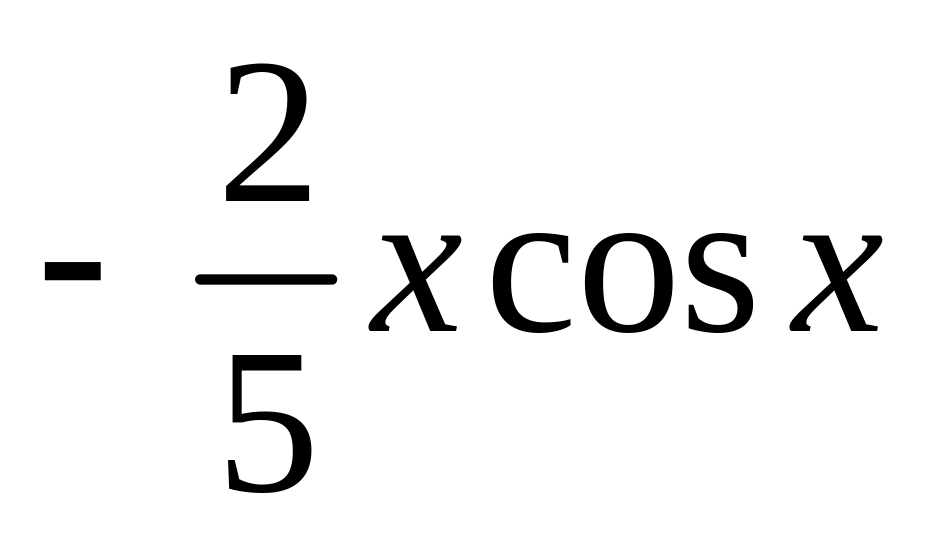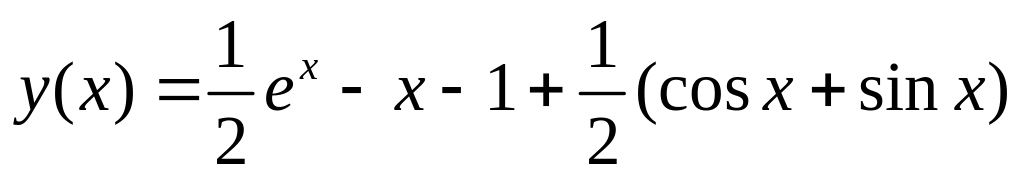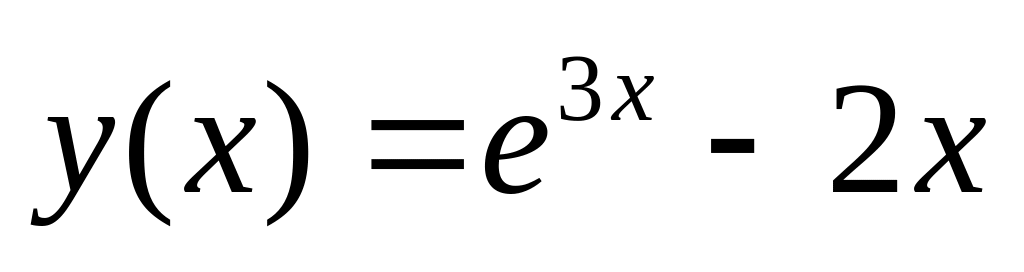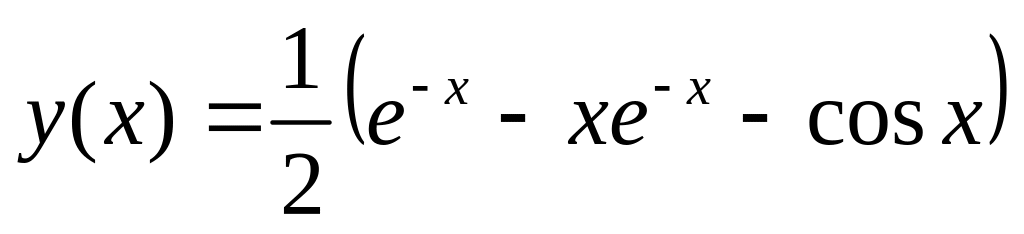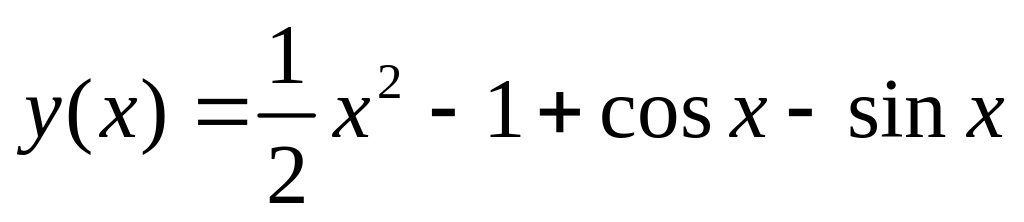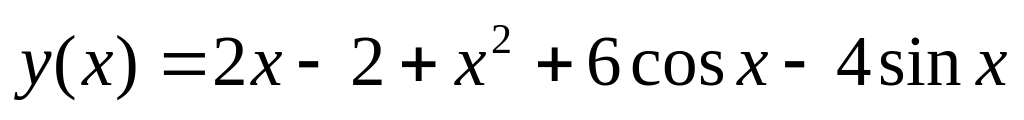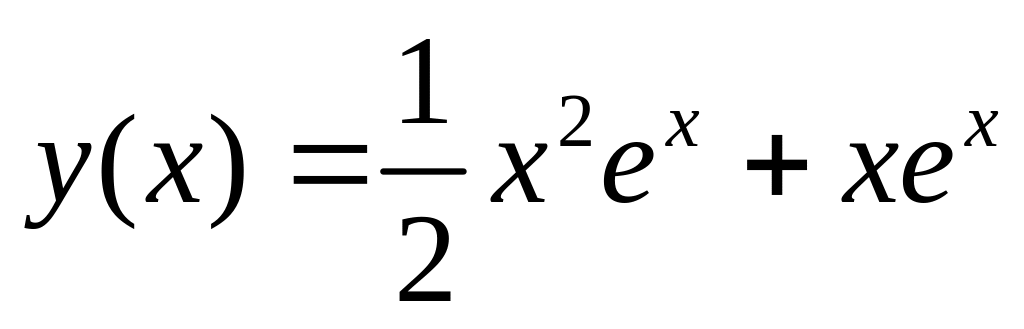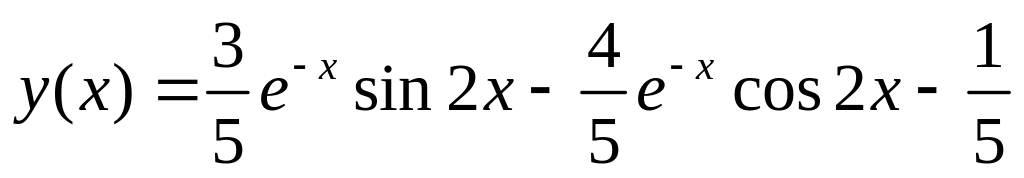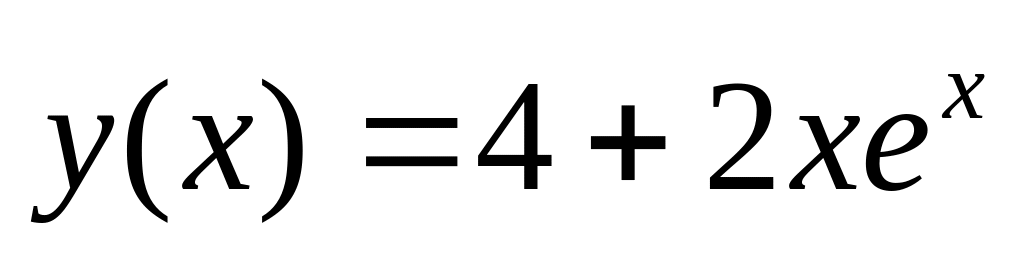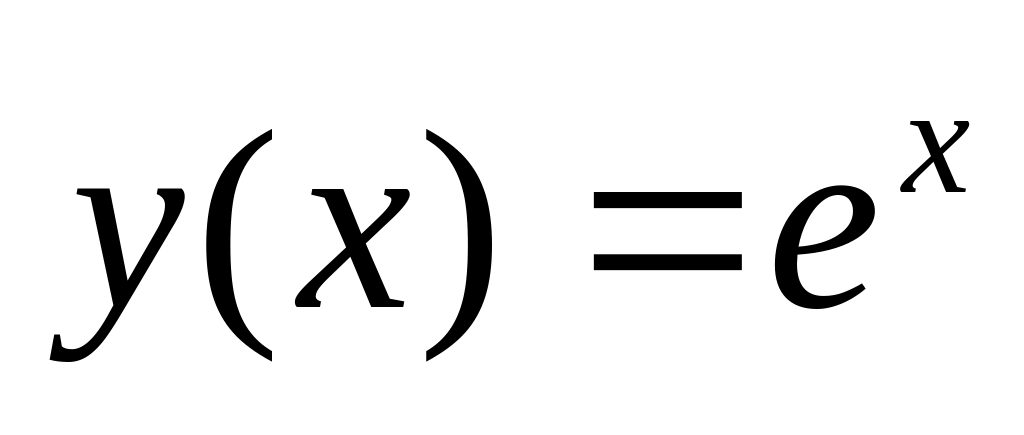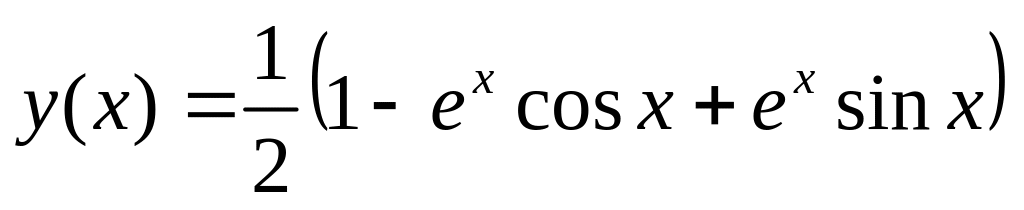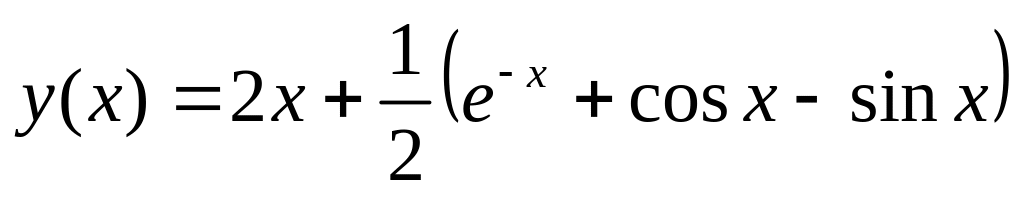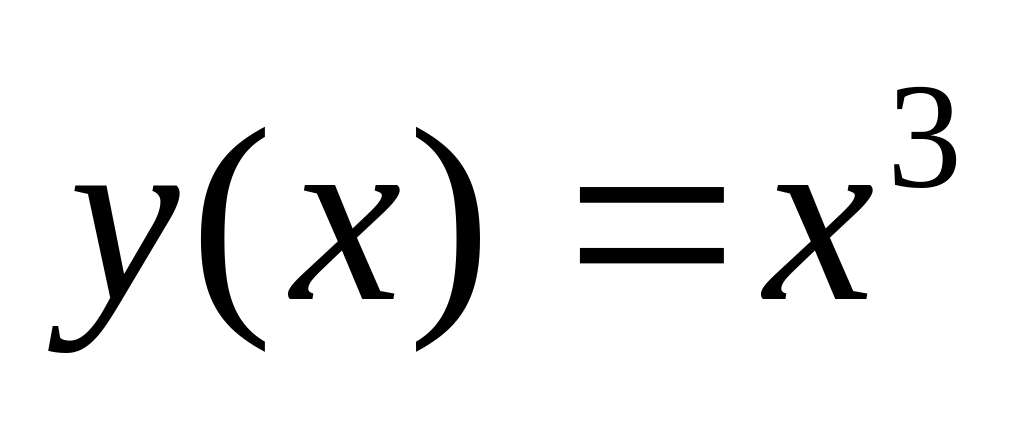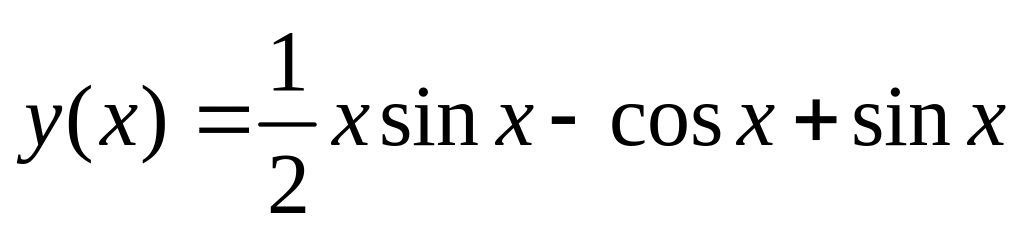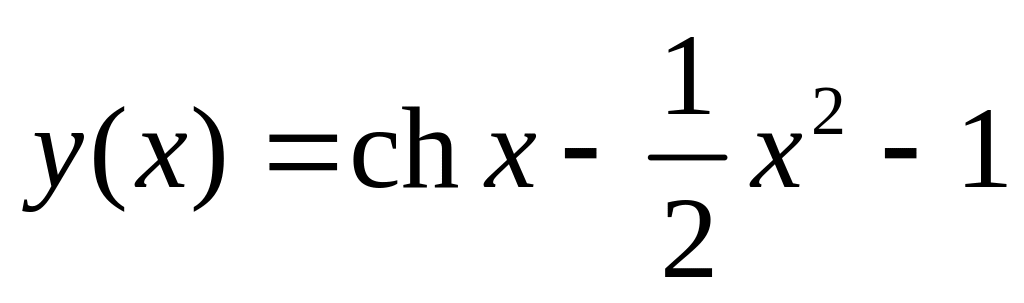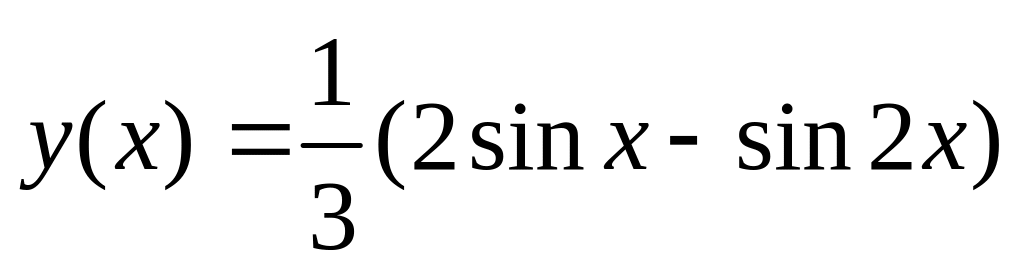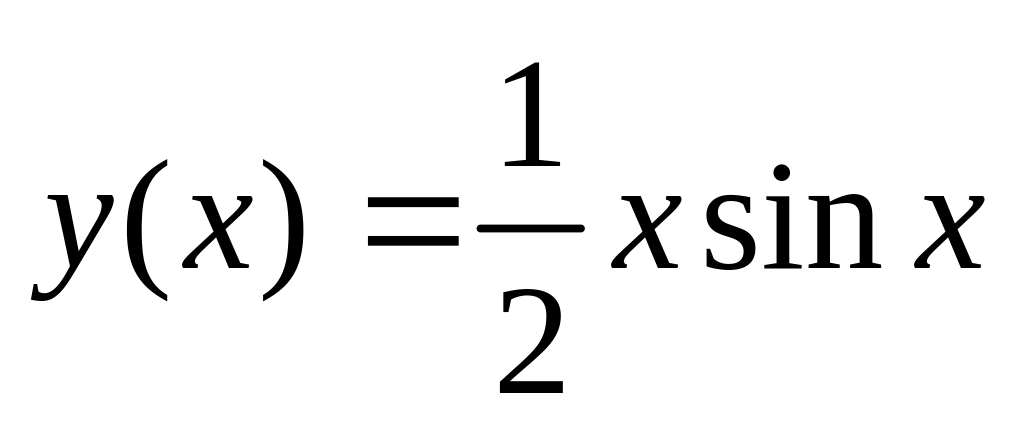
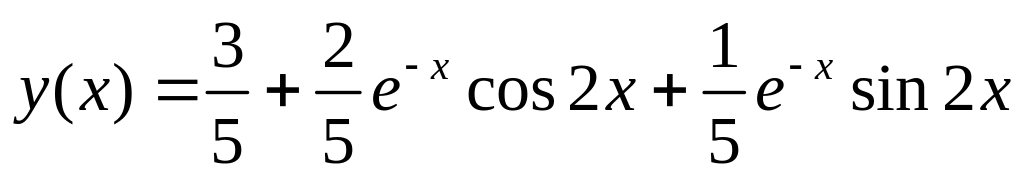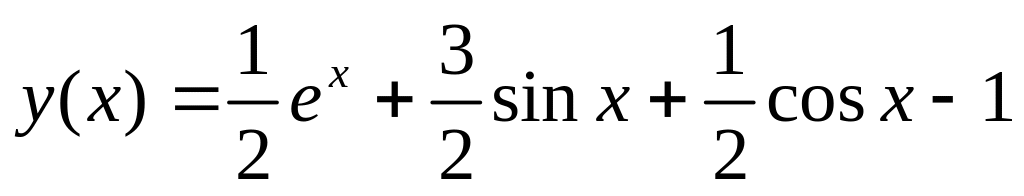
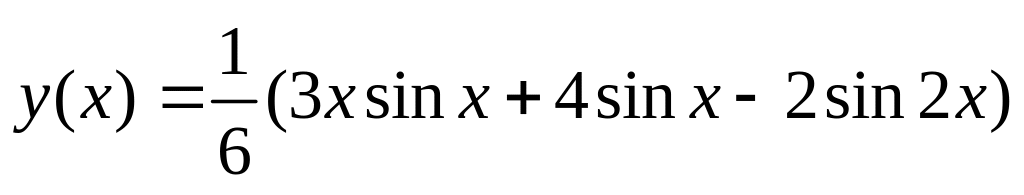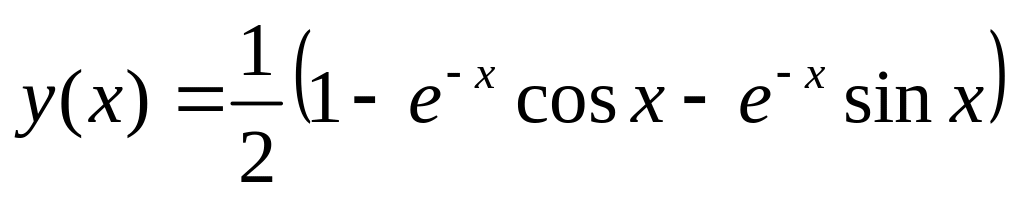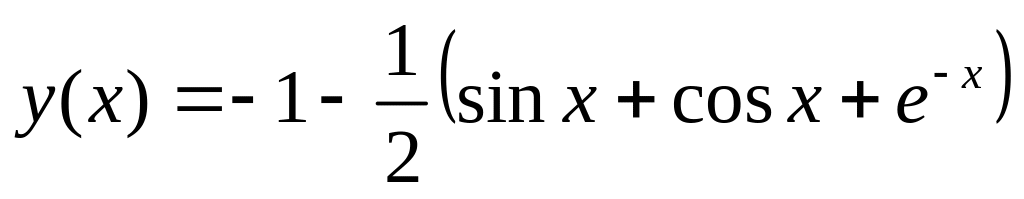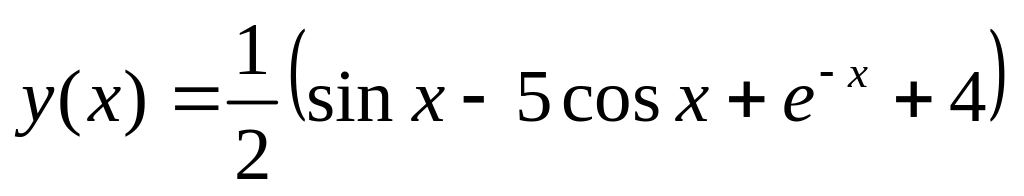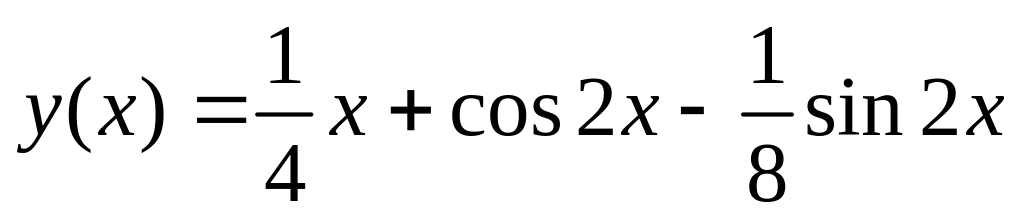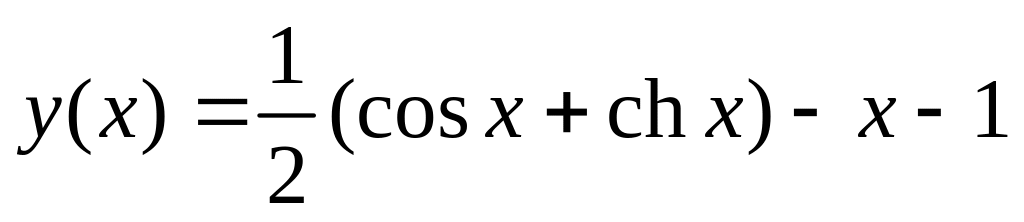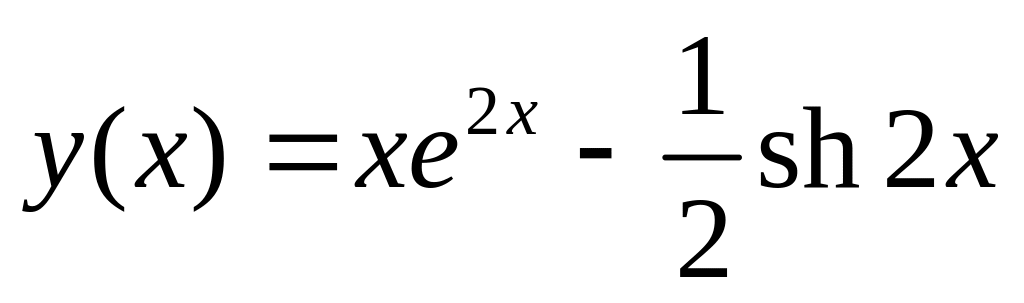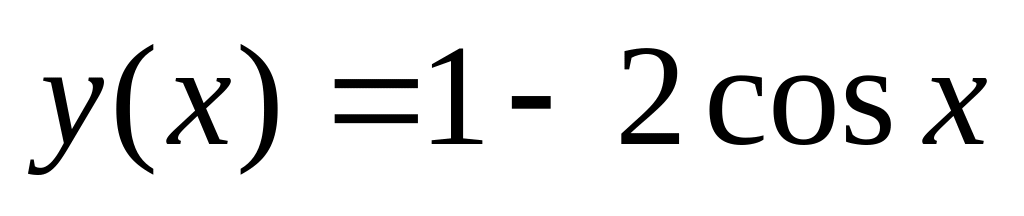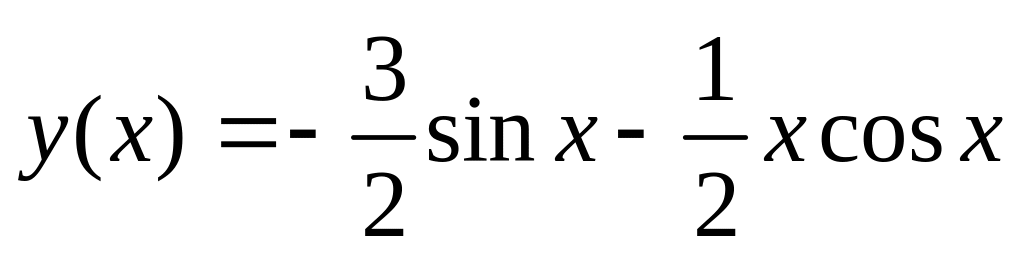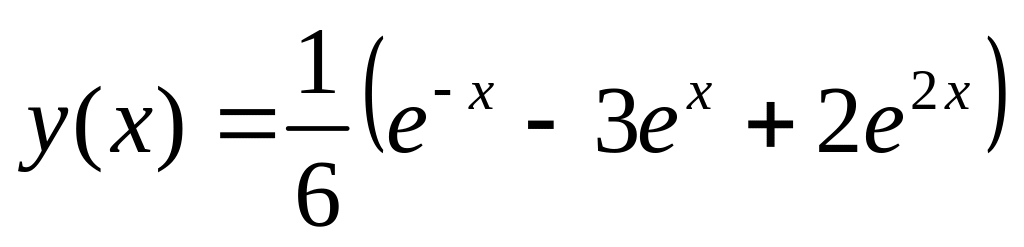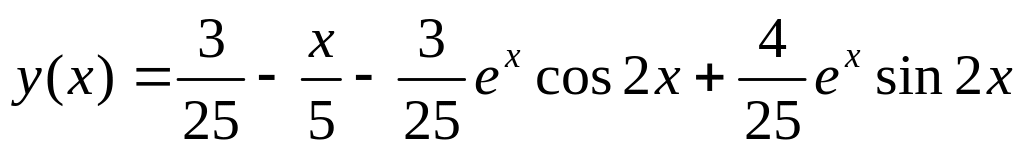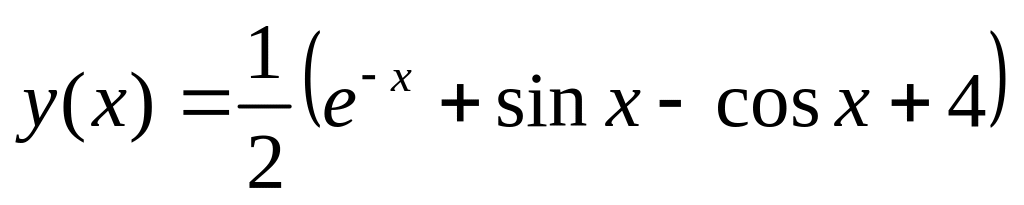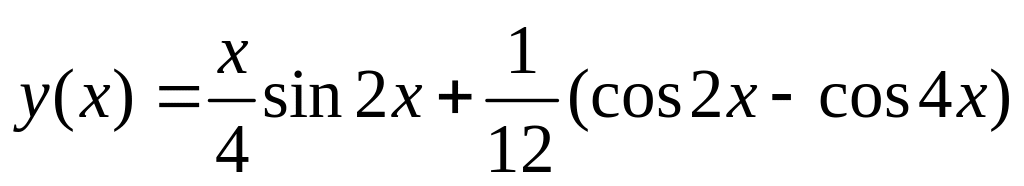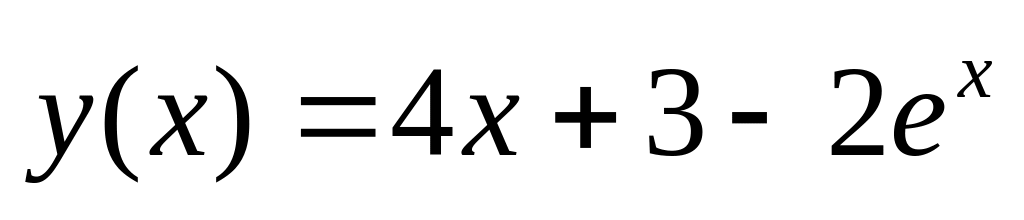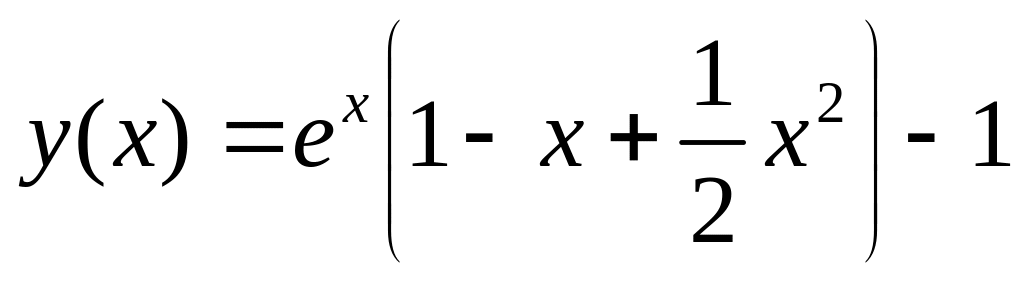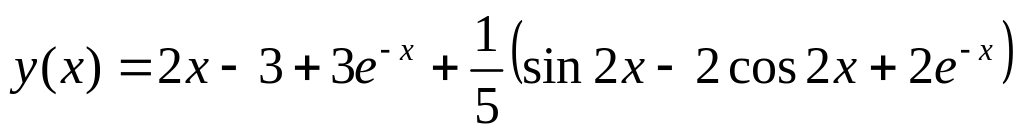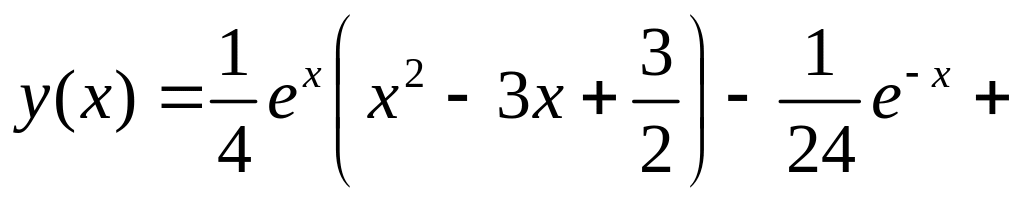
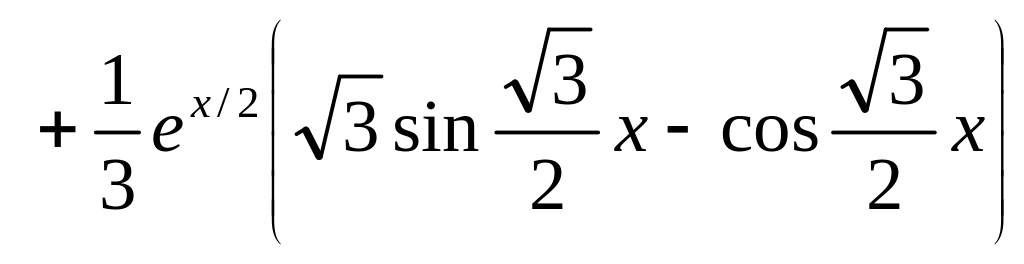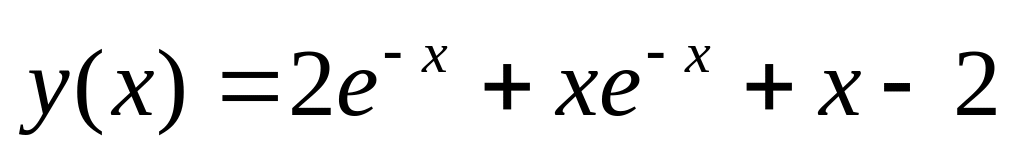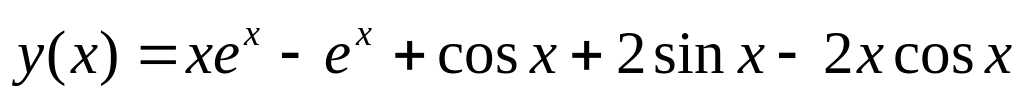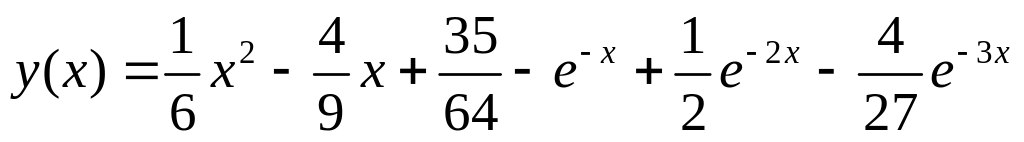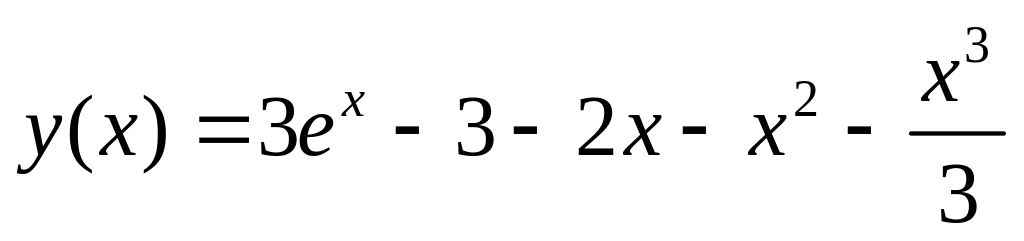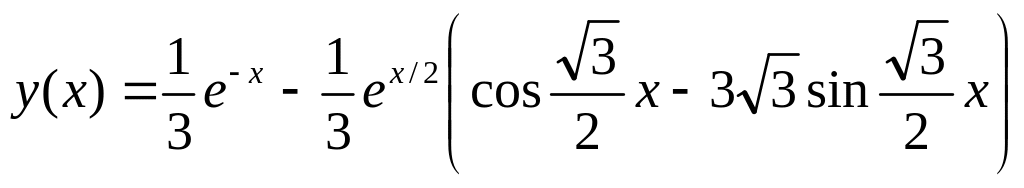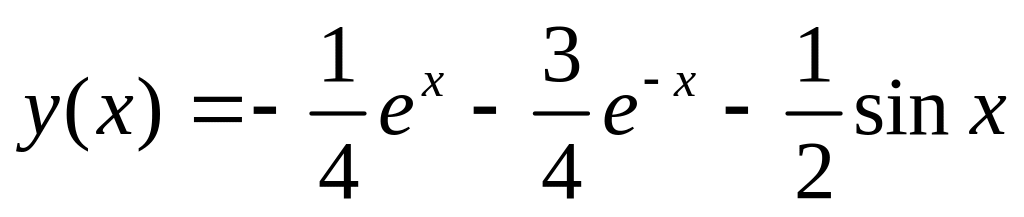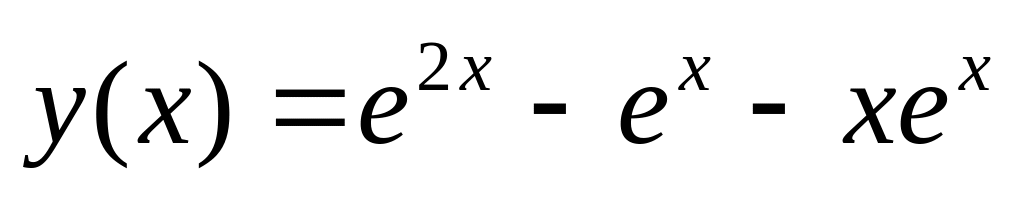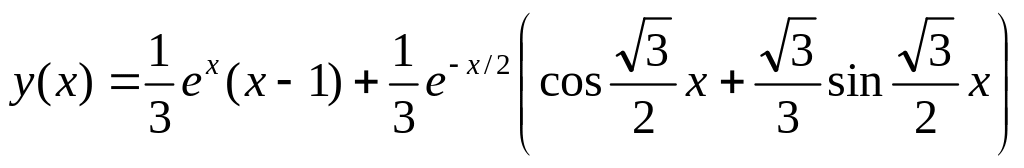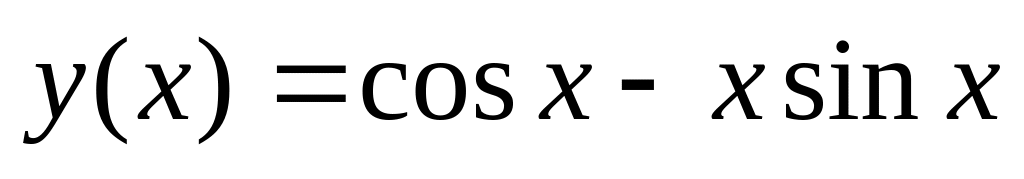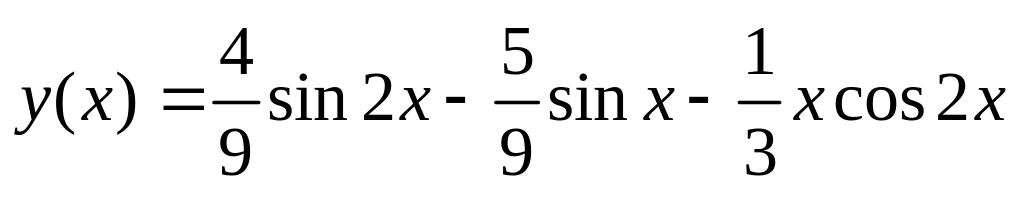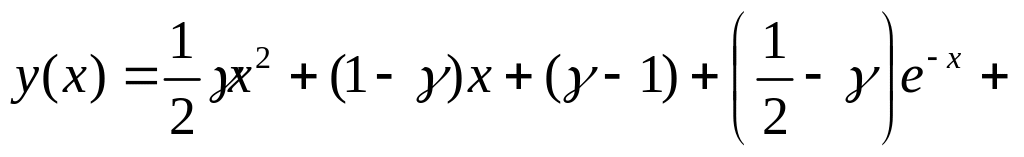
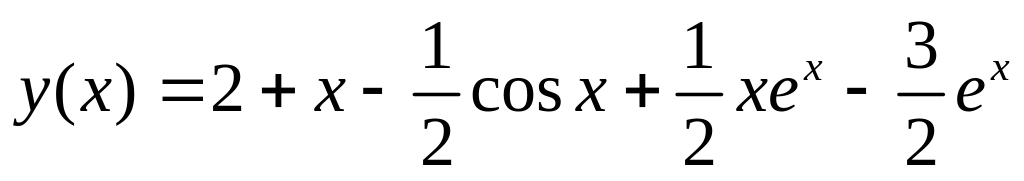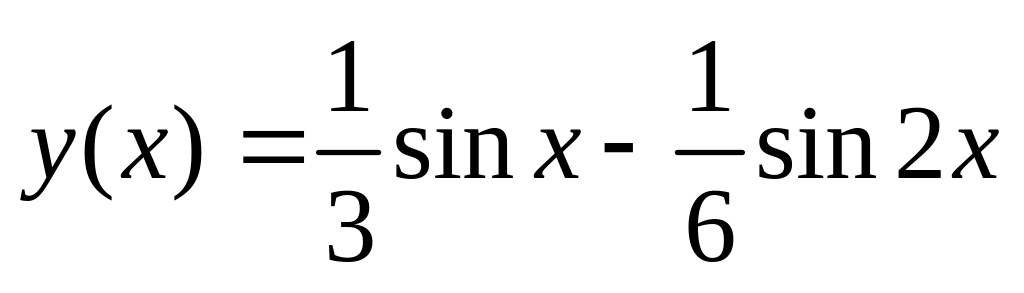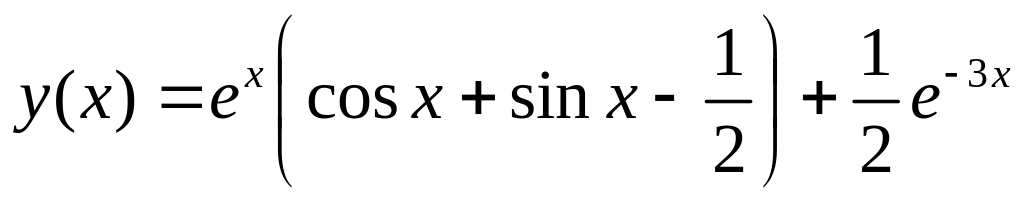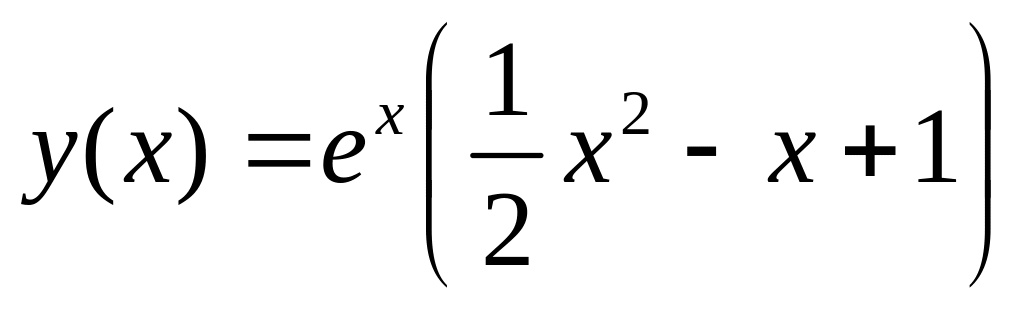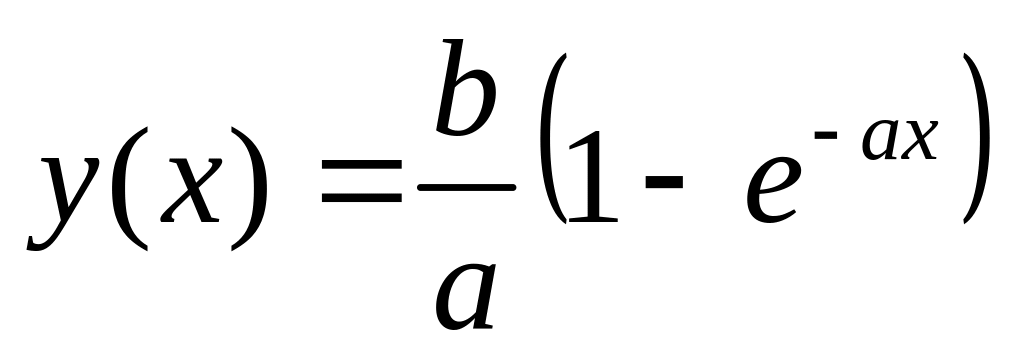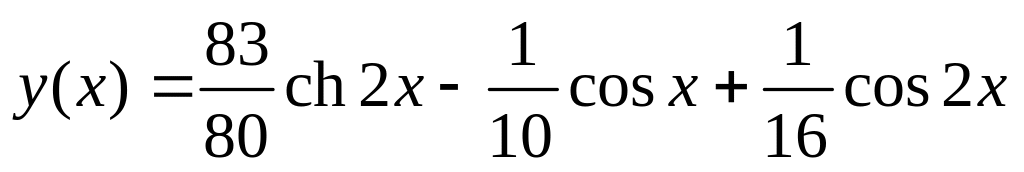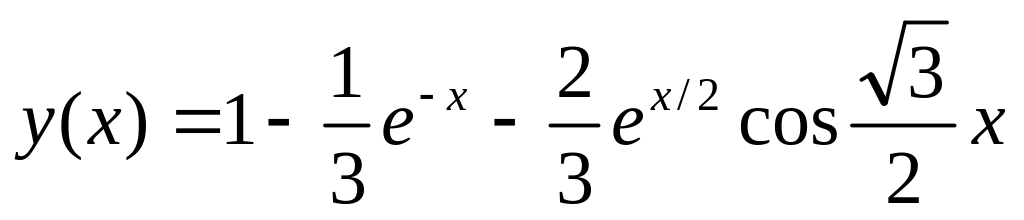Литература по операционному исчислению

1. Ван-дер Поль Б., Бремер Х. Операционное исчисление на основе двустороннего преобразования Лапласа. — М.: ИЛ, 1952.

2. Диткин В.А., Кузнецов П.И. Справочник по операционному исчислению. — М.–Л., 1951, 256 с.

3. Диткин В.А., Прудников А.П. Интегральные преобразования и операционное исчисление. — М.: Физматгиз, 1961.

4. Диткин В.А., Прудников А.П. Интегральные преобразования и операционное исчисление. — М.: Физматгиз, 1974, 542 с.

5. Карслоу Х., Егер Д. Операционные методы в прикладной математике. — М.: ИЛ, 1948.

6. Кожевников Н.И., Краснощекова Т.И., Шишкин Н.Е. Ряды и интегралы Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа. — М.: Наука, 1964.

7. Краснов М.Л., Макаренко Г.И. Операционное исчисление. Устойчивость движения. — М.: Наука, 1964, 103 с.

8. Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного, операционное исчисление, теория устойчивости. Задачи и упражнения. — М., 1971, 255 с.

9. Микусинский Я. Операторное исчисление. — М.: ИЛ, 1956.

10. Римский-Корсаков Б.С. Операционное исчисление. — М., 1960.

11. Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа. — М.: Наука, 1980, 336 с.

12. Шахно К.У. Элементы теории функций комплексной переменной и операционного исчисления. Учебное пособие. —Л.: изд. СЗПИ, 1961.

13. Шелковников Л.А., Такайшвили К.Г. Сборник упражнений по операционному исчислению. — М.: Высшая школа, 1961, 154 с.

14. Шостак Р.Я. Операционное исчисление. — М., 1968, 192 с.

Содержание

Применение интеграла Дюамеля к интегрированию дифференциальных уравнений 3

По правилу дифференцирования интеграла по параметру 3

Их операторные решения 4

Применив интеграл Дюамеля, решить дифференциальные уравнения 6

Интегрирование дифференциальных уравнений с переменными (функциональными) коэффициентами 8

Тогда уравнение в изображениях 8

Выберем ветвь корня, для которой 9

О функциях с запаздывающим аргументом и их изображениях 9

Изображение 11

3 12

Изображение 13

Интегрирование дифференциальных уравнений, содержащих в правой части функцию Хевисайда 14

Найдем 15

Имеем 15

Окончательно 15

Дифференциальные уравнения с запаздывающим аргументом 16

Решение. Перейдем к изображениям 17

Решение интегральных уравнений 18

Решение. В изображениях 21

Разлагая на простейшие дроби, найдем оригиналы 22

Решение нестационарных задач математической физики 22

Начальные скорости равны нулю. Найти отклонения при . 23

Индивидуальные задания по теме «Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами операционным методом» 26

Ответы для индивидуальных заданий по теме «Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами операционным методом» 30

Литература по операционному исчислению 35