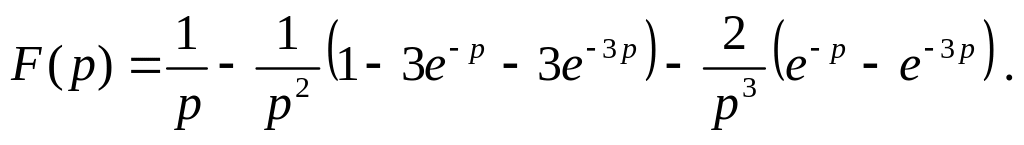- •Применение интеграла Дюамеля к интегрированию дифференциальных уравнений
- •Интегрирование дифференциальных уравнений с переменными (функциональными) коэффициентами
- •О функциях с запаздывающим аргументом и их изображениях
- •Интегрирование дифференциальных уравнений, содержащих в правой части функцию Хевисайда
- •Дифференциальные уравнения с запаздывающим аргументом
- •Решение интегральных уравнений
- •Решение нестационарных задач математической физики
- •Индивидуальные задания по теме «Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами операционным методом»
- •Ответы для индивидуальных заданий по теме «Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами операционным методом»
- •Литература по операционному исчислению
Применение интеграла Дюамеля к интегрированию дифференциальных уравнений
Интеграл Дюамеля (формула 18 пункта 5.7) может быть использован при интегрировании дифференциальных уравнений.
Выведем формулу для интеграла Дюамеля.
Пусть
![]()
![]()
![]()
![]() По
теореме умножения изображений (формула
(17) пункта 5.6) имеем:
По
теореме умножения изображений (формула
(17) пункта 5.6) имеем:
![]()
![]() .
(30)
.
(30)
По теореме о дифференцировании оригинала (правой части (30)) по формуле пункта 5.10:
![]()
![]() .
.
По правилу дифференцирования интеграла по параметру
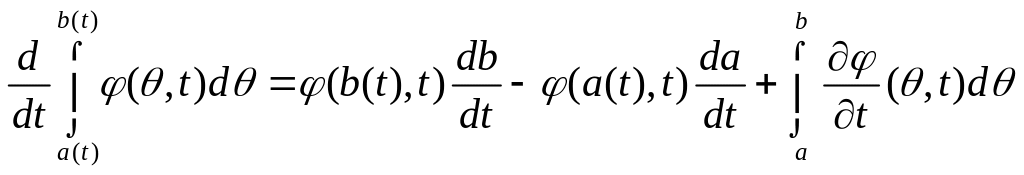 (31)
(31)
получим
![]() (32)
(32)
Правую часть этой формулы называют интегралом Дюамеля. В силу равноправности функций f и g ее можно записать и так
![]()
![]() (33)
(33)
Применим интеграл Дюамеля к интегрированию дифференциальных уравнений. Пусть требуется найти решение линейного дифференциального уравнения с постоянными коэффициентами
![]() , (34)
, (34)
удовлетворяющее
нулевым (для простоты) начальным условиям
![]()
![]() (35)
(35)
Наряду с этим уравнением будем рассматривать дифференциальные уравнения с такой же левой частью, но правой частью, равной 1: (метод толчков)
![]() (36)
(36)
и будем искать его решение, также удовлетворяющее нулевым начальным данным
![]() . (37)
. (37)
Эти дифференциальные уравнения переходят в уравнения в изображениях
![]()
![]()
Их операторные решения
![]() (38)
(38)
где
![]() .
.
Из них выражаем
![]() .
Используя формулу (32)
.
Используя формулу (32)
![]()
![]() . (39)
. (39)
Если известно решение z(t) уравнения (36) , то по (39) мы получим решение x(t) в виде квадратур.
Пример 105. Найти
решение дифференциального уравнения
![]() при начальных условиях
при начальных условиях
![]()
Решение.
Сначала найдем решение
![]() ,
удовлетворяющее условиям
,
удовлетворяющее условиям
![]() .
Его уравнение в изображениях
.
Его уравнение в изображениях
![]() дает
дает
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Для отыскания
решения исходного уравнения применим
формулу (39). Имеем![]() ,
так что
,
так что
![]() .
.
Замечание. Особенно удобно применять интеграл Дюамеля для интегрирования нескольких дифференциальных уравнений с одинаковыми левыми и различными правыми частями. В этом случае интеграл Дюамеля значительно сокращает объем вычислительной работы.
Пример 106. Решить дифференциальное
уравнение
![]() c начальными условиями
c начальными условиями
![]() .
.
Решение.
Сначала решим задачу Коши для
дифференциального уравнения
![]() ,
,
![]() .
Его уравнение в изображениях
.
Его уравнение в изображениях
![]() имеет решение
имеет решение
![]() .
Отсюда
.
Отсюда
![]() .
По формуле Дюамеля (32)
.
По формуле Дюамеля (32)
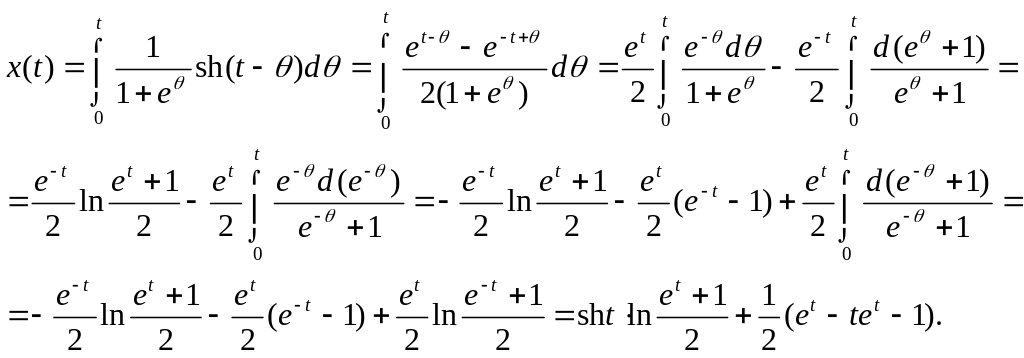
Применив интеграл Дюамеля, решить дифференциальные уравнения
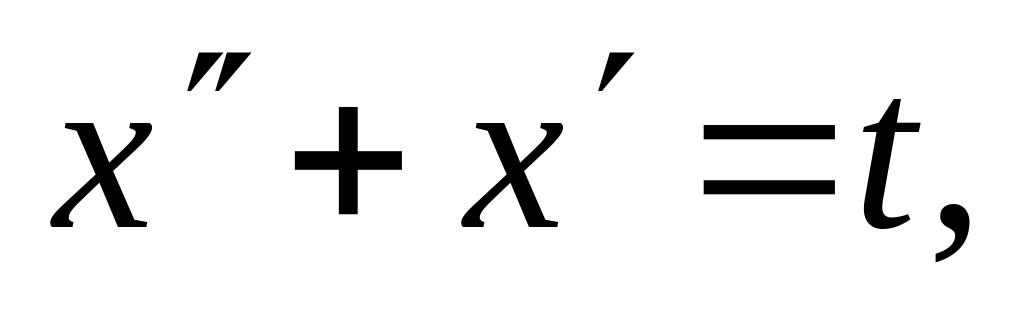
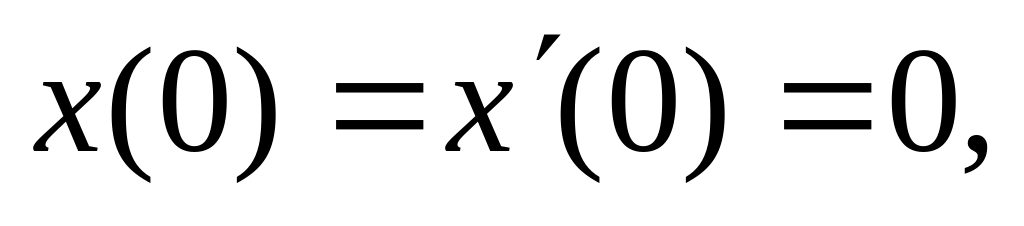 ответ:
ответ: 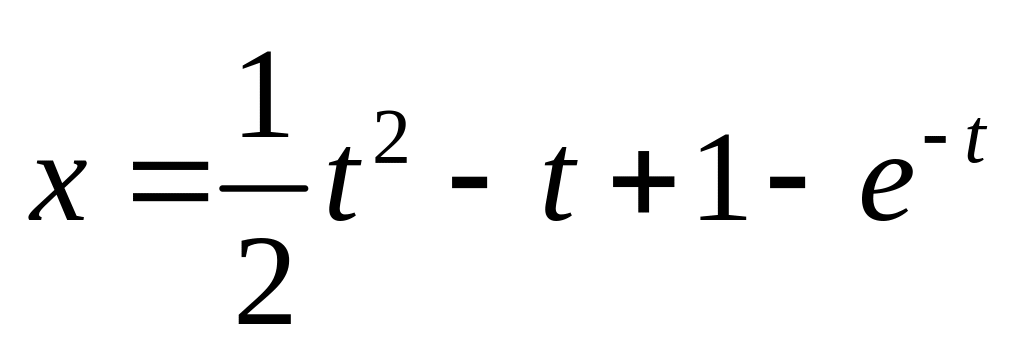 .
.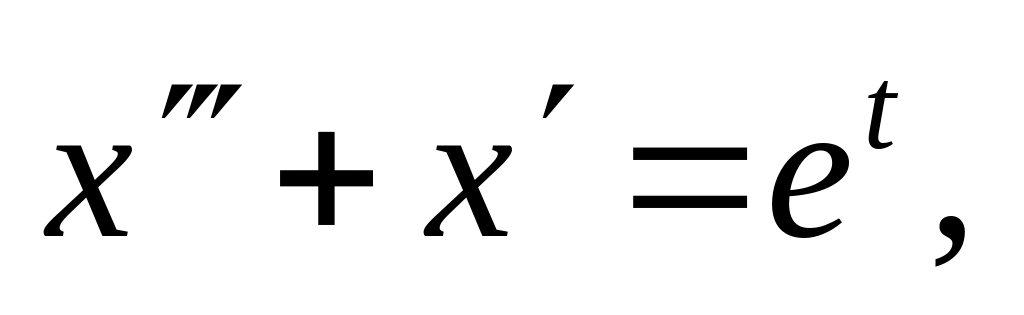
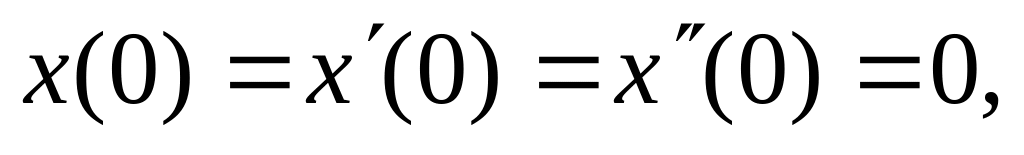
ответ: ![]() .
.
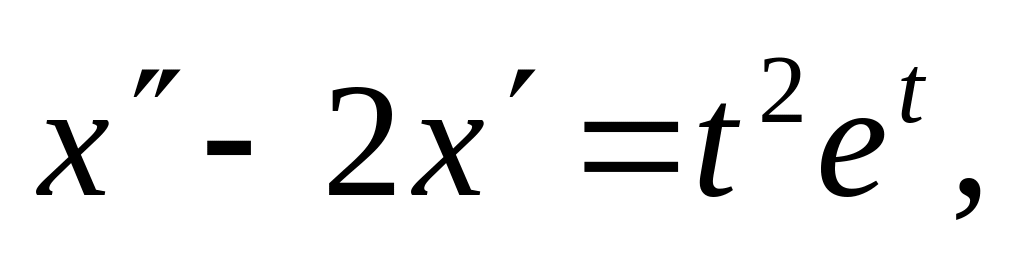 ответ:
ответ: 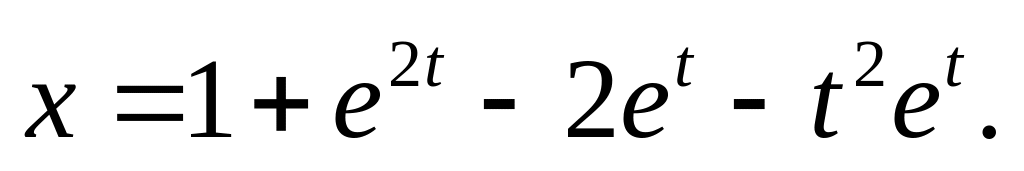
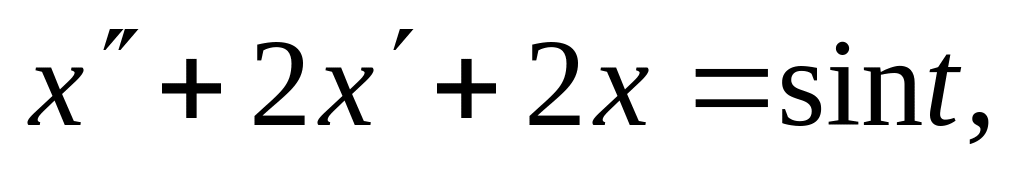
ответ: ![]()
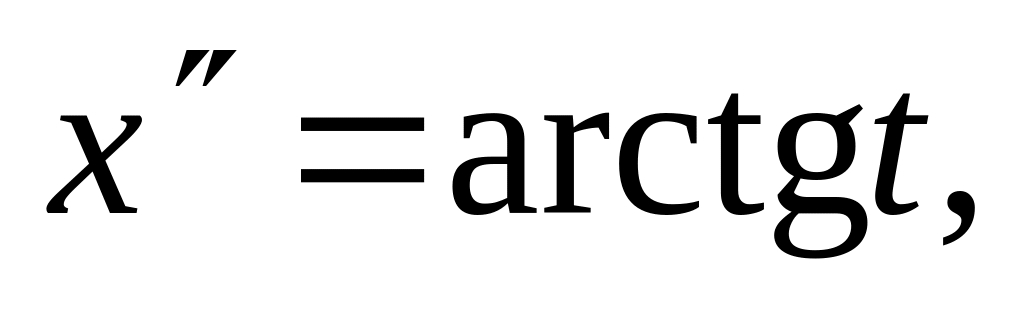
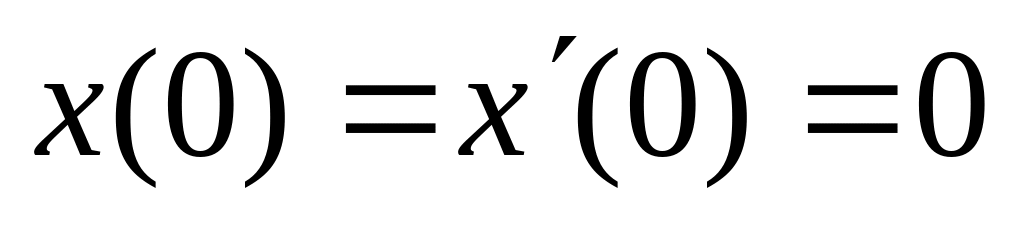 ,
,
ответ: ![]()
ответ: ![]()
ответ:
![]()
![]() .
.
ответ: ![]() .
.
ответ: ![]() .
.
ответ: ![]() .
.
ответ: ![]()
ответ:
![]()
![]() .
.
ответ: ![]() .
.
Интегрирование дифференциальных уравнений с переменными (функциональными) коэффициентами
Пример
120. Решить дифференциальное
уравнение Бесселя
![]() с начальными условиями
с начальными условиями
![]()
![]()
Решение. Перейдем к изображениям
![]()
![]()
![]()
![]()
![]()
![]()
![]() Для нахождения изображений
Для нахождения изображений
![]() и
и
![]() воспользуемся формулой дифференцирования
изображений (формула (23) пункта 5.11)
воспользуемся формулой дифференцирования
изображений (формула (23) пункта 5.11)
![]()
![]() Тогда
Тогда
![]() ,
,
![]() .
.
Тогда уравнение в изображениях
![]() ,
,
![]()
Уравнение с разделяющимися переменными
![]()
![]()
![]()
![]()
Выберем
ветвь корня, для которой
![]()
![]()
![]()
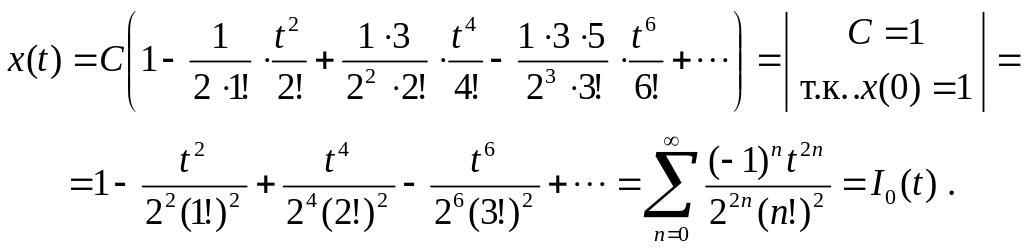
![]() — так называемая функция Бесселя
нулевого порядка.
— так называемая функция Бесселя
нулевого порядка.
О функциях с запаздывающим аргументом и их изображениях
Как уже было сказано
в пункте 2, единичная функция Хевисайда
![]() может превратить в оригинал любую
функцию f (t),
“выключая” ее значения при t < 0
и сохраняя при t > 0:
может превратить в оригинал любую
функцию f (t),
“выключая” ее значения при t < 0
и сохраняя при t > 0:
![]()
Имеется большое
количество функций
![]() ,
которые описывают процессы, начинающиеся
не в
,
которые описывают процессы, начинающиеся
не в
![]() ,
а с опозданием τ > 0.
С помощью функции Хевисайда
,
а с опозданием τ > 0.
С помощью функции Хевисайда
![]()
функцию с запаздыванием записывают так
![]() (40)
(40)
Заметим, что
множитель
![]() способен
“включать” или “гасить” значения
некоторых функций. Эта функция удобна
для записи как периодических, так и
других составных функций.
способен
“включать” или “гасить” значения
некоторых функций. Эта функция удобна
для записи как периодических, так и
других составных функций.
По теореме запаздывания (пункт.5.3) изображения этих оригиналов (40) выражаются формулой
![]()
![]()
![]() (41)
(41)
Пример 121.Найти
изображение периодического с периодом
Т прямоугольного импульса
![]() величины А и продолжительностью τ
величины А и продолжительностью τ


A 
![]()
![]()
![]()
![]()
![]()
![]()
Решение.
Постоянная функция
![]() должна быть “погашена”, начиная с
момента
должна быть “погашена”, начиная с
момента
![]() .
Это можно записать как
.
Это можно записать как
![]()
Далее с момента
![]() опять “включаем” функцию
опять “включаем” функцию
![]() и
“гасим” ее в момент
и
“гасим” ее в момент
![]() В этом случае следует записать
В этом случае следует записать
![]() и т. д.
и т. д.
Окончательно
![]()
Изображение
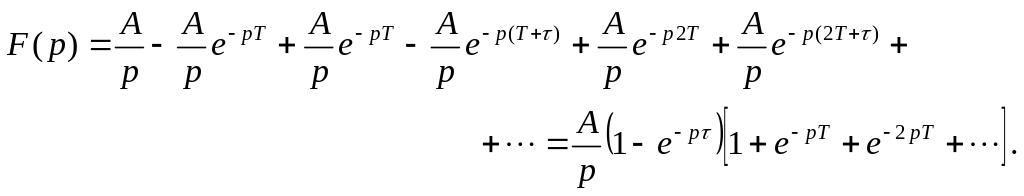
Так как
![]() то
суммируя геометрическую прогрессию в
квадратных скобках со знаменателями
то
суммируя геометрическую прогрессию в
квадратных скобках со знаменателями
![]() ,
получим
,
получим
![]()
Этот же результат можно было бы получить по формулам (20), (21).
Пример 122. Построить
график функции
![]() и найти ее изображение.
и найти ее изображение.
Решение. Функция
![]() описывает некоторый процесс, “включаемый”
с запаздыванием
описывает некоторый процесс, “включаемый”
с запаздыванием
![]() .
Для того, чтобы решить, какой это процесс,
нужно функцию представить в форме
.
Для того, чтобы решить, какой это процесс,
нужно функцию представить в форме





![]()
![]()
![]()
![]() 3
3
2 t
Пример 123. Найти изображение составной функции , предварительно записав ее с помощью функции Хевисайда одним аналитическим выражением.
Функция имеет вид и график .


 3
3
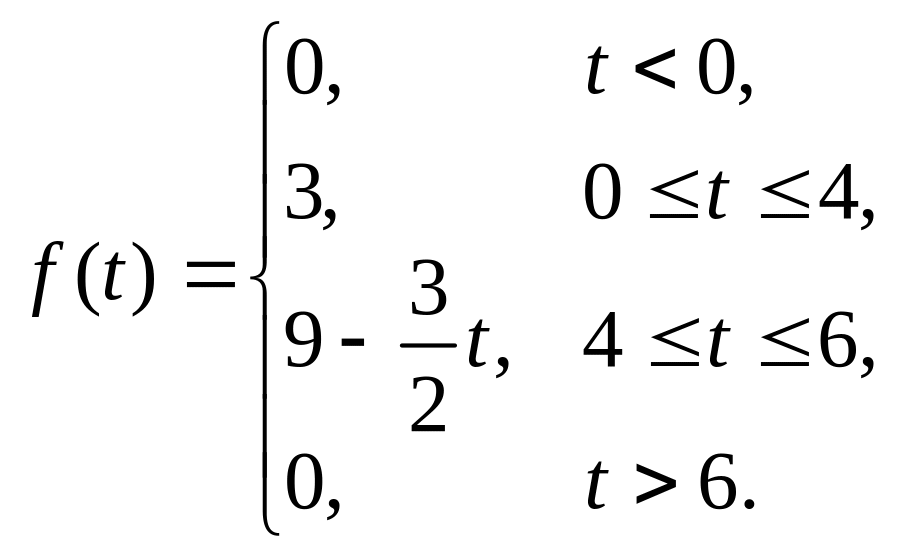
 t
t

 0 4 6
0 4 6
Решение. Функция
![]() при
при
![]() .
В момент
.
В момент
![]() “включается” функция, равная 3. В момент
“включается” функция, равная 3. В момент
![]() она “гасится” и “включается” функция
она “гасится” и “включается” функция
![]() .
В момент
.
В момент
![]() “гасится” эта функция. Эту последовательность
действий можно описать формулой
“гасится” эта функция. Эту последовательность
действий можно описать формулой
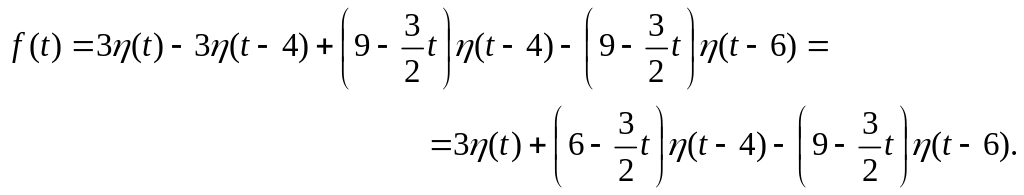
Надо “организовать”
сдвиги аргумента
в множителях при функциях Хевисайда:
во втором слагаемом надо получить
аргумент
![]() ,
а в третьем
,
а в третьем
![]() :
:
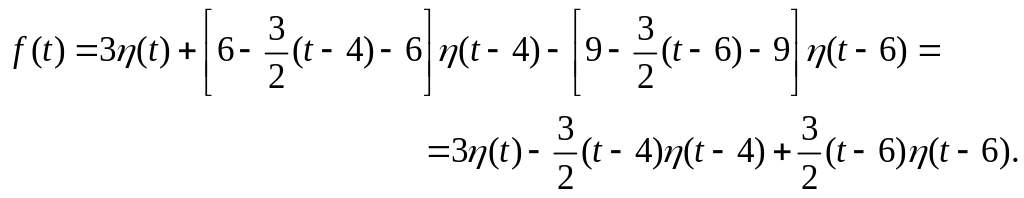
Изображение
![]()
В следующих задачах,
записав с помощью функции Хевисайда
одним аналитическим выражением составную
функцию
![]() найти ее изображение:
найти ее изображение:
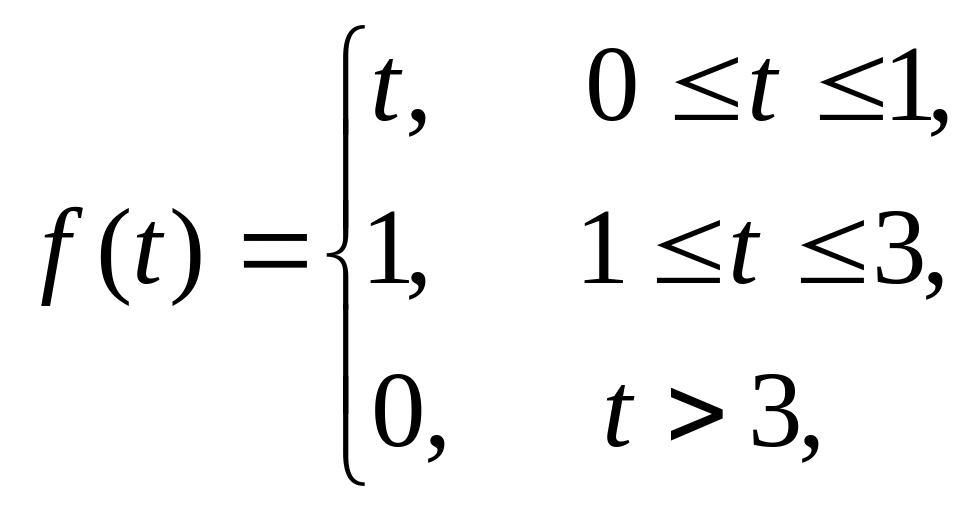 ответ:
ответ: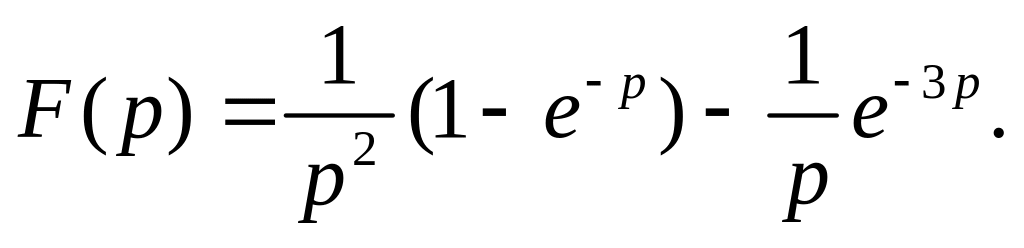
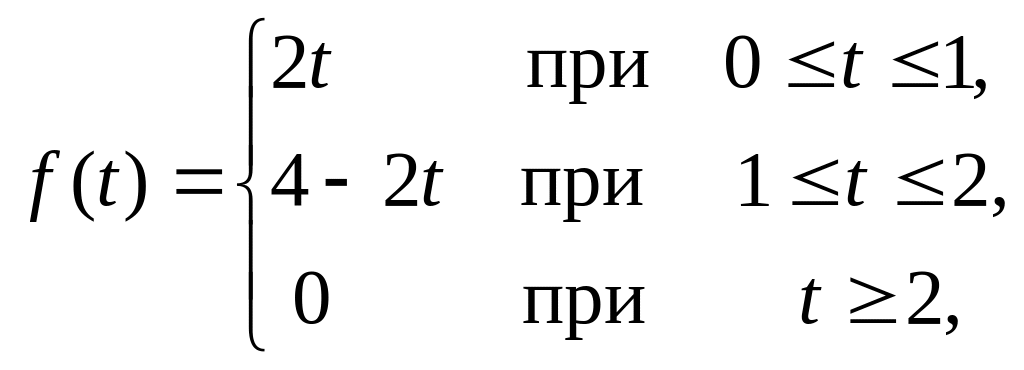 ответ:
ответ:
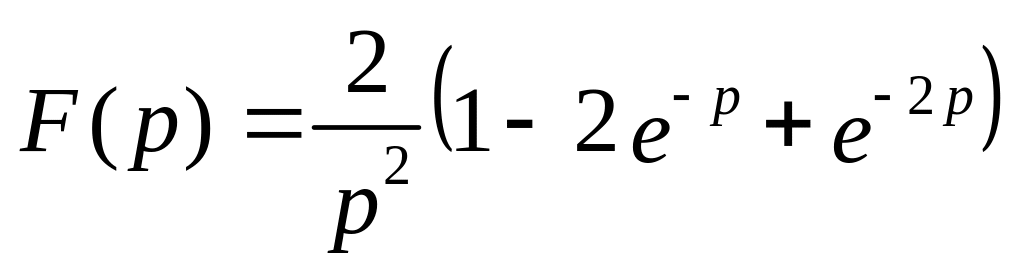 .
.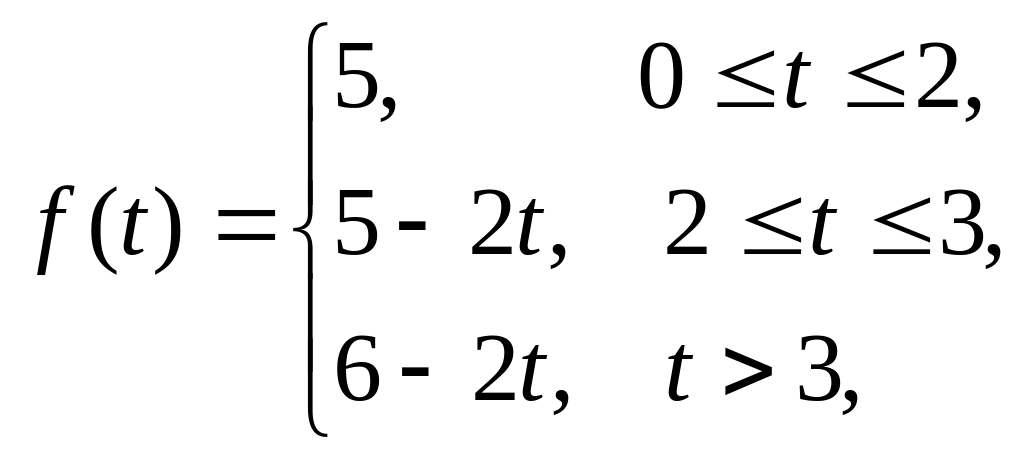 ответ:
ответ:
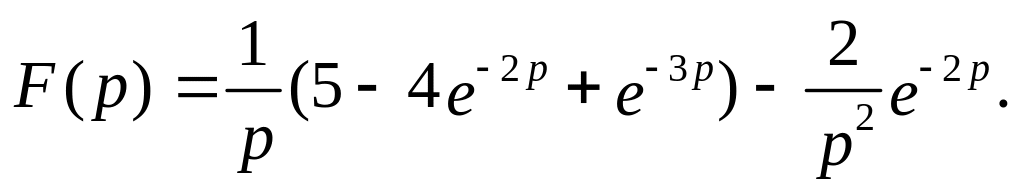
В следующих задачах
записать функцию
![]() в виде, удобном для построения графика,
и найти её изображение.
в виде, удобном для построения графика,
и найти её изображение.
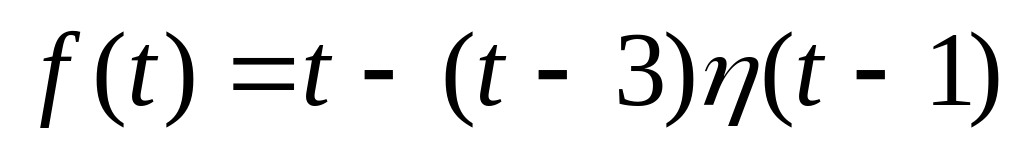 ,
,
ответ:
![]()
![]() .
.
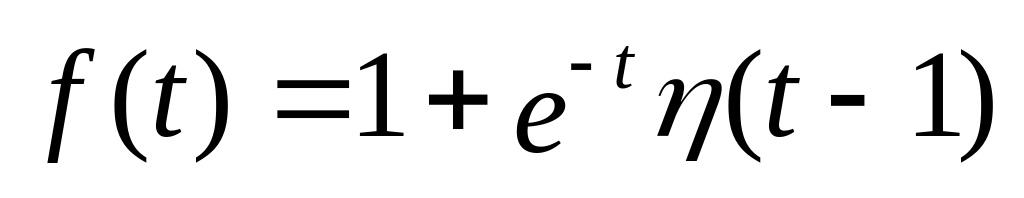 ,
,
ответ:
![]()
![]() .
.
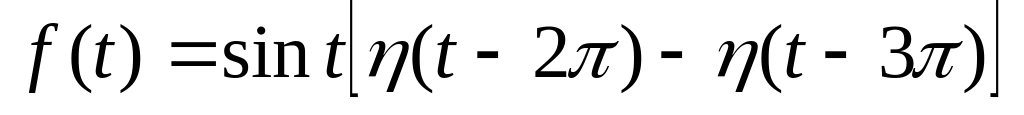 ,
,
ответ:
![]()
![]() .
.
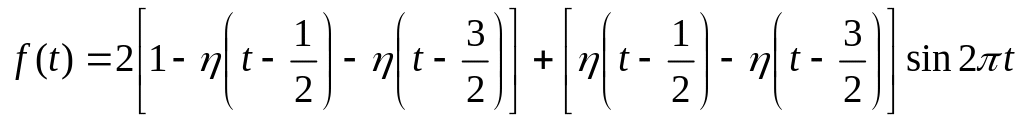 ,
,
ответ:
![]()
![]() .
.
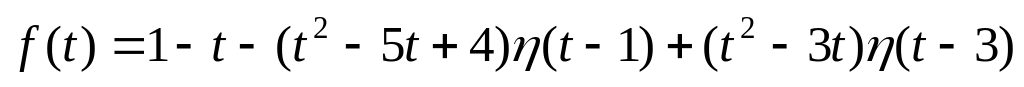 ,
ответ:
,
ответ: