3.6. Завдання для самостійної роботи

1. За допомогою алгоритма прямої прогонки, знайти найкоротший шлях між вершинами 1 і 9 мережі, зображеної на рис. 14.

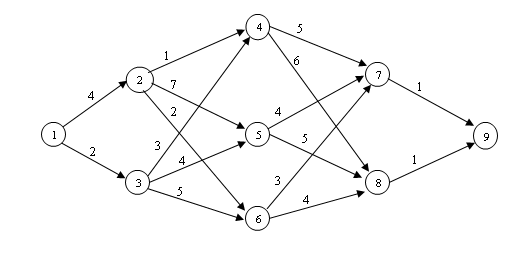
Рис. 14

Відповідь: найкоротший шлях 1—2—6—7—9, довжина шляху 10.

2. За допомогою алгоритма прямої прогонки, знайти найкоротший шлях між вершиною A й однієї з вершин останнього слою (вершинами G, H або I) наступної мережі (рис. 15).

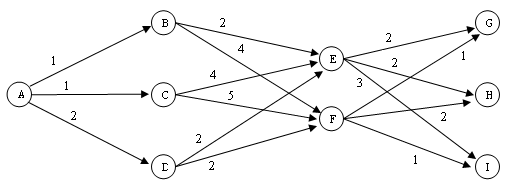
Рис. 15

Відповідь: найкоротші шляхи: A—B—E—G; A—D—F—G; A—D—F—I, їх довжина 5.

3.7 Схема алгоритму зворотної прогонки (азп) по дугах, що входять

1. Покласти ; .

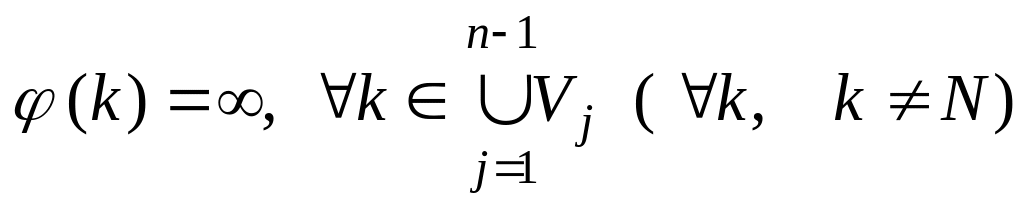( - допоміжний масив. У ньому будемо зберігати поточну довжину найкоротшого шляху від всіх вершин не останнього слою. Початкове значення цієї довжини вважаємо рівним ).

2. Планування кроку

1. Виділити всі можливі стани, які можуть мати місце наприкінці кроку : всі

2. . Для кожного стану виконати наступне:

По кожній дузі (k,s), що входить у вершину знайти

3. Вважаємо

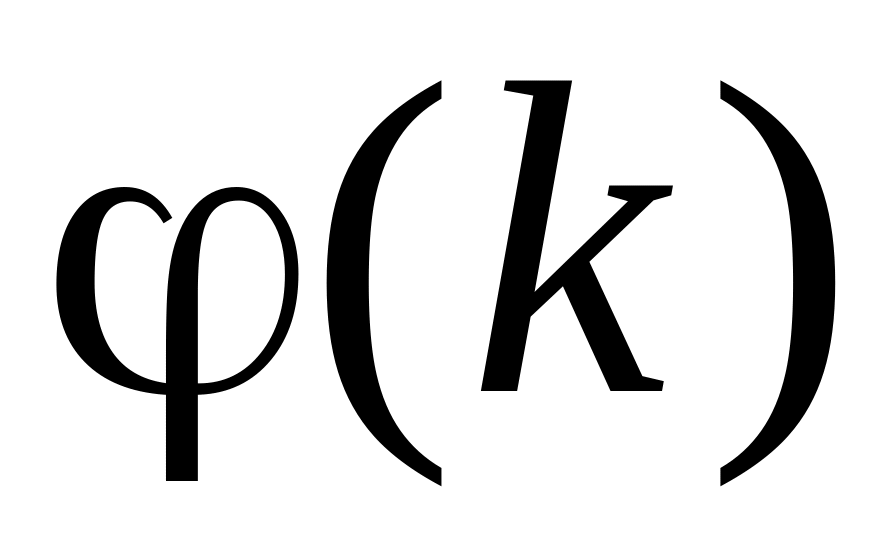
3. j=j –1. Якщо j=0, то перейти до пункту 4, інакше – перейти до пункту 2.

4. Формування оптимального розв’язку.

Процес розв’язку ЗЗНШ АЗП по дугах, що входять, проілюстрований на рис. 16.

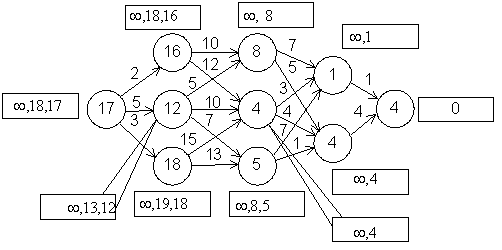
Рис. 16

У прямокутниках вказані значення, що послідовно принімалися величинами .

3.8 Відмінності алгоритмів прямої і зворотної прогонок

Вибір того чи іншого напрямку розрахунків (що співпадає з напрямком мережі або є зворотнім до нього) залежить від постановки вихідної задачі ЗНШ. Розглянемо чотири можливі ситуації, що впливають на цей вибір.

1. Потрібно знайти найкоротшу відстань між двома конкретними вершинами мережі. У цьому випадку вибір може бути довільним, тому що жоден з алгоритмів не має переваги над іншим.

2. Потрібно знайти найкоротшу відстань між вершиною 1 і однією з вершин множини

.

У цьому випадку рекомендується застосовувати АЗП і у пункті 1 алгоритму вважати, що .

3. Потрібно знайти найкоротшу відстань між однією з вершин множини і вершиною . У цьому випадку рекомендується застосовувати АПП і у пункті 1 вважати, що .

4. Потрібно знайти найкоротшу відстань у мережі такого типу (рис. 17):

							S finish
S start

Рис. 17

тобто від однієї (довільної) з вершин із множини до однієї (довільної) з вершин множини . У цьому випадку вибір напрямку прогонки довільний.

Для випадків 1 і 4 схеми АПП й АЗП розв’язку ЗЗНШ еквівалентні.

Отже, у загальному випадку, для розв’язку задач ДП можливе застосування чотирьох алгоритмів (зворотньої і прямої прогонки по дугах, що виходять і входять). Для розв’язку задачі ЗНШ обрати можна кожний з них. Однак, при розв’язанні деяких інших задач динамічного програмування можливі ситуації, коли відмінності між цими алгоритмами, пов'язані з ефективністю обчислень, виявляються істотними. Алгоритми по дугах, що виходять можна узагальнити й використати для розв’язання задач, у яких є елемент випадковості. Для алгоритмів по дугах,що входять цього зробити не можна.

Досвід практичного застосування АЗП показує, що процедура зворотньої прогонки більш ефективна.