2 Основні положення поетапного оптимального управліНня

Пошук екстремума функції багатьох змінних замінюється багаторазовим пошуком екстремума функції однієї або невеликої кількості змінних: . Інакше кажучи, планування багатокрокового процесу, розбивається на ряд етапів, на кожному етапі оптимізується тільки один крок. Але це не означає, що, обираючи управління на одному окремому кроці, можна не враховувати інші. Навпаки, управління на кожному кроці повинно обиратися з урахуванням всіх його наслідків. Плануючи багатоепну операцію, ми повинні обирати управління на кожному кроці, виходячи не з вузьких інтересів саме цього кроку, а виходячи з більш широких інтересів операції в цілому.

Проілюструємо принцип “далекоглядного” планування [1]. Для цього повернемося до прикладу про концерн. У ньому планується робота групи підприємств на період часу років, і кінцева мета - одержання максимального об'єму продукції деякого товару. На початку періоду є певний запас засобів виробництва (машин, устаткування), за допомогою якого можна почати виробництво цього товару. Кроком планування є рік. Щороку керівництво концерну має вирішувати три питання:

• скільки закуповувати сировини;

• скільки коштів виділити на ремонт і закупівлю нового обладнання,

• як розподілити їх між підприємствами.

При “короткозорому” поетапному плануванні ми б прийняли таке рішення: вкласти максимальну кількість коштів у закупівлю сировини і використати все наявне устаткування на повну потужність, прагнучи максимального об'єму продукції до кінця першого ж року (рис. 2). До чого призведе таке планування? До швидкого зношування машинного парку і, як наслідок, до того, що на другому році випуск продукції зменшиться.

О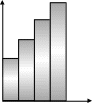 б'єм випуску продукції Об'єм випуску

продукції

рік рік

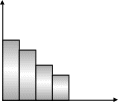
Рис. 2 Рис. 3

При “далекоглядному” плануванні, навпаки, будуть передбачені заходи, що забезпечують поповнення машинного парку в міру його зношування. З урахуванням таких капіталовкладень об'єм продукції за перший рік буде меншим, ніж міг би бути, але буде забезпечена можливість розширення виробництва в наступні роки (рис. 3).

!	У процесі поетапного планування управління на кожному кроці повинно вибиратися з урахуванням його майбутніх наслідків.

Серед усіх кроків є крок, який можна планувати без урахування його наслідків - це останній крок. Його можна планувати таким чином, щоб він сам по собі приносив найбільшу користь. Спланувавши оптимальним чином цей крок, можна приступати до планування передостаннього кроку і т.д. Тому, процес ДП звичайно проходить у зворотному за часом напрямку: від кінця до початку.

!	Отже, першим планується останній крок.

Однак, заздалегідь не відомо, чим закінчується передостанній крок. Тому потрібно зробити припущення про те, чим може закінчитися передостанній крок і для кожного із цих припущень обрати найкраще управління, яке будемо називати умовним оптимальним управлінням.

!	У методі ДП на кожному кроці для кожного з можливих результатів попереднього кроку знаходиться умовне оптимальне управління.

Отже, важливою умовою застосування ДП є можливість розбиття процесу прийняття рішення на ряд однотипних кроків або етапів, кожний з яких планується окремо, але з урахуванням результатів, отриманих на інших кроках. Деякі операції природно розпадаються на етапи, в інших розбиття на етапи доводиться проводити штучно.