2.2. Коэффициент Пуассона и модуль сдвига для однонаправленно армированных композиционных материалов
При растяжении происходит
уменьшение диаметра образца (или –
ширины, толщины). При деформации стержня
относительная продольная деформация
.
Причем
.
Абсолютная величина
называется коэффициентом Пусассона.
Следовательно по определению коэффициент Пуассона композиции
(2
13)
При нагружении силой Рх
и деформацию ук
можно рассчитать из соотношения (2.11) с
учетом того, что:
;
:
(2.14)
Подставив в формулу (2.13) выражение (2.14) и используя условия (2.1), получим уравнение для определения коэффициента Пуассона
(2.15)
Сдвиг – вид деформации, при котором все слои смещаются параллельно друг другу (рис. 2.2). Отрезок АА1 характеризует абсолютный сдвиг. При малых углах tg =AA1/АД; это соотношение принято называть относительным сдвигом.
Закон Гука для деформации при сдвиге:
,
где:
– напряжения;
G – модуль сдвига.
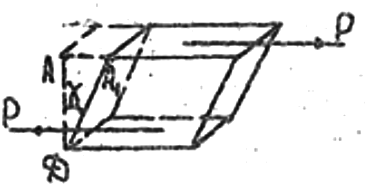
Рис. 2.2. Схема деформации образца при сдвиге
При нагружении армированного КМ касательными напряжениями (рис. 2.2) нагрузка воспринимается матрицей и волокнами последовательно, в силу чего касательные напряжения в матрице хум и волокнах хув одинаковы:
(2.16)
При этом деформация сдвига КМ, по аналогии с уравнением (2.11), определяется соотношением
(2.17)
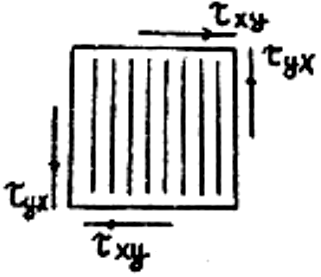
Рис. 2.3. Схема касательных напряжений в однонаправленном КМ
Поскольку поведение всех компонентов рассматривается в пределах упругих деформаций, можно воспользоваться выражением закона Гука для сдвига: ( = /G), – подставив которое в уравнение (2.17), с учетом равенства {2.16) получим модуль сдвига КМ при деформации в плоскости ху:
(2.18)
Таким образом, четыре упругие константы Ехк, Еук, хук и Gхук – полностью описывают упругое поведение рассматриваемой модели однонаправленного армированного КМ при плоском напряженном состоянии.
Соотношение (2.6), (2.12), (2.15), (2,18) можно рассматривать только как приближенные, оценочные, поскольку модель для их расчета очень идеализирована. Технологические дефекты, неоднородности распределения волокон по объему, искажения их сечений, разориентация и разброс свойств компонентов приводят к тому, что реальные характеристики армированных КМ отличаются от расчетных. Поэтому для паспортизации КМ используют экспериментально определенные упругие константы.
2.3. Прочность км, армированных непрерывными и дискретными волокнами
2.3.1. Композиционные материалы, армированные непрерывным волокном
Развитие методов расчета прочности изделий и конструкций из КМ основывается на использовании следующих трех принципов: 1) расчетная модель и созданные на ее основе методы расчета должны исходить из форм исчерпания несущей способности изделия и должны быть подтверждены экспериментально; 2) упрощающая гипотеза о свойствах материала, конструкции и эксплуатационных нагрузках должна обеспечивать некоторый запас прочности, однако без излишнего увеличения массы или преждевременного разрушения; 3) методы расчета должны допускать определенное варьирование свойств и структуры материала с тем, чтобы можно было оптимизировать конструкцию, прежде всего по основному критерию – минимуму массы.
Сложность строения КМ и существенные отличия в их поведении при деформировании и разрушении по сравнению с традиционными конструкционными материалами приводит к необходимости использования методов математического модулирования с помощью ЭВМ. В связи с этим при оптимизации конструкций из КМ получили применение частные критерии: равнопрочность волокон, безмоментное состояние, максимум критических нагрузок, минимум отклонения спектра собственных частот колебаний от заданных и др.
В связи с этим в настоящее время расчеты на прочность изделий из КМ с учетом их оптимизации при проектировании разработаны лишь для простых видов нагружения.