Диаграмма расслоения

Кривая расслоения отделяет диаграмме гомогенную от гетерогенной области (гетерогенная область заштрихована косой чертой).

К – критическая точка.

Особенность системы в критической точке – равенство состава двух равных фаз.

Теоретические основы перегонки

Всю перегонку делят на два вида:

1. простая перегонка (отгонка). В этом случае чаще всего отделяется жидкая часть от растворенных в ней твердых веществ. Пример: дистилляция воды.

2. Фракционная перегонка, в которой происходит разделение двух жидкостей.

Любая перегонка основана на первом законе Коновалова, который гласит:

пар, обогащается более легколетучим компонентом, входящим в состав кипящей жидкости.

Фракционная перегонка включает в себя несколько стадий:

1. Кипячение исходного раствора для получения пара определенного состава.

2. Конденсация полученного пара.

3. Кипячение полученного пара для получения пара, ещё более обогащенного легколетучим компонентом.

4. Конденсация полученного пара.

Количество подобных операций зависит от необходимости получить чистые вещества.

Основная проблема при подобной перегонки – изменение состава кипящей жидкости и получающегося пара в результате кипения.

Если система образует азеотропную смесь, то разделить ее на чистые компоненты невозможно (даже теоретически).

Второй закон Коновалова гласит:

В точках азеотропа состав кипящей жидкости и пара совпадают, поэтому в результате перегонки бинарного раствора, образующего азеотропную смесь, одним из продуктов перегонки будет являться азеотроп.

Лекция № 10

План лекции:

1. Диаграммы плавкости.

2. Уравнение Шредера.

3. Теория построения диаграмм плавкости.

4. Основы термического анализа. Кривые охлаждения.

Диаграммы плавкости

Полное название подобных диаграмм – диаграмма состояния двухкомпонентной системы температура – состав, содержащих твердую и жидкую фазы двух неограниченно смешивающихся друг с другом жидкостей и твердых веществ, образующих твердые растворы и химические соединения.

В данном случае фазовое равновесие можно рассматривать как псевдохимическую реакцию . Очевидно, что в условиях равновесия, химические потенциалы двух реагентов будут равны.

В случае однокомпонентной системы - растворимость вещества при данной температуре.

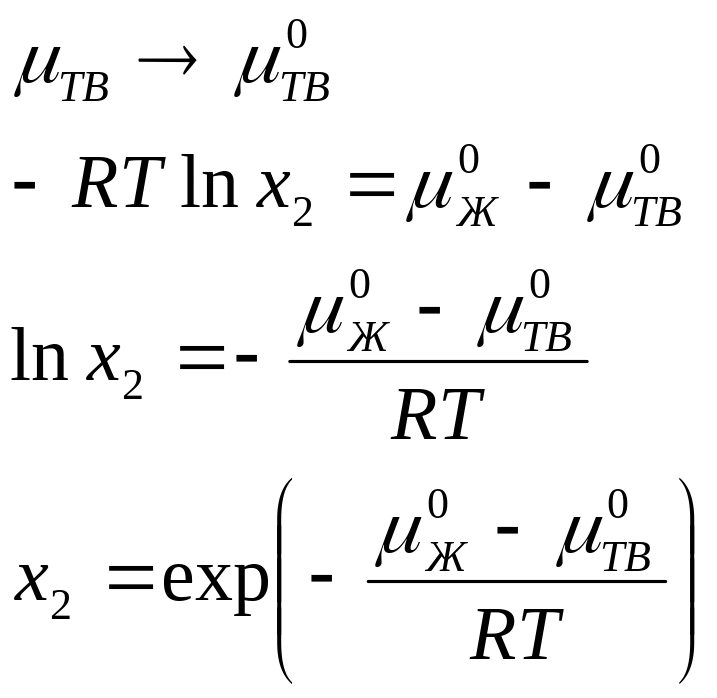
В данном случае растворимость вещества будет численно равна константе равновесия процесса плавления. В том случае, если образующийся состав будет идеальным.

Уравнение Шредера

Данное уравнение является аналогом уравнения изобары, записанным для процесса плавления:

- дифференциальная форма уравнения Шредера.

Если образующийся расплав обладает идеальными свойствами:

- теплота плавления.

Если раствор неидеальный, вместо растворимости используют константу равновесия, а вместо теплоты плавления - теплота, равная теплоте смешения двух жидкостей: расплавленного компонента А и идеального раствора.

Величина будет аналогична полезной теплоте смешения, то есть тепловыделение или теплопоглощение в процессе перехода данного моль твердого вещества в состояние насыщенного раствора.

Анализ уравнения Шредера аналогичен анализу уравнения изобары.

1. Идеальный раствор:

2. Неидеальный раствор:

Поэтому, влияние температуры на растворимость веществ может быть различная. Уравнение Шредера служит основой для теоретического построения диаграмм плавкости.