Параметры гидромотора (насоса)

Расход Q	Давление p	Вращающий момент Mгм	Частота вращения nгм	Угловая скорость ωгм	Рабочий объём Wгм
л/мин	МПа	Н∙м	об/мин	рад/c	см3

С учётом единиц измерения параметров, представленных в табл. 2, формула (27) не изменится, а формула (28) примет вид:

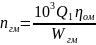. (29)

В общем случае характеристика простого трубопровода, содержащего гидродвигатель (гидроцилиндр или гидромотор), в соответствии с уравнением (21) предстанет в виде:

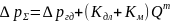, где m = 1 или m = 2.

(30)

Составим характеристику простого трубопровода с гидродвигателем, изображённого на рис. 3. Заменим гидравлическую схему трубопровода (участок от сечения 3 – 3 до сечения 4 – 4) эквивалентной схемой, в которой на участке трубопровода длиной l и диаметром d в условном виде представим все виды местных гидравлических сопротивлений (рис. 7).

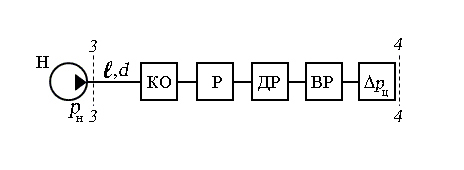
Рис. 7. Эквивалентная схема простого трубопровода, содержащего гидродвигатель:

р_н – давление насоса; КО – клапан обратный; Р – распределитель; ДР – дроссель; ВР - внезапное расширение; ∆р_ц – потери в гидроцилиндре, связанные с нагрузкой на штоке G и усилием противодействия пружины F_пр

Составим уравнение потерь давления (характеристику простого трубопровода, содержащего гидроцилиндр) в виде (30). Для этого определим потери давления по длине трубопровода и в местных сопротивлениях (потери на обратном клапане, на распределителе, дросселе, при внезапном расширении и на преодоление сил сопротивления ∆р_ц). Пусть режим течения в трубопроводе – ламинарный, потери на обратном клапане и распределителе заданы коэффициентами сопротивления ζ_ко и ζ_рс, потери на дросселе заданы коэффициентом расхода μ_р и площадью проходного сечения S₀.

Потери давления по длине определим по формуле (15):

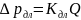, где .

Потери давления в местных сопротивлениях в соответствии с формулами (16), (17), (26):

- на обратном клапане (16) ∆р_ок = , где K_ок = ζ_ок ;

- на распределителе (16) ∆р_рс = , где K_рс = ζ_рс ;

- на дросселе (17) . где ;

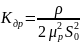- при внезапном расширении (16) ∆р_вр = 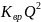, где K_вр = ζ_вр ;

- потери давления (26) .

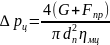Сложив все виды потерь, получим:

,

,

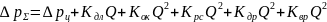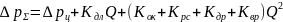или

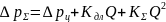. (31)

Выражение (31) называется характеристикой простого трубопровода с гидродвигателем. Графическое отображение характеристики изображено на рис. 8.

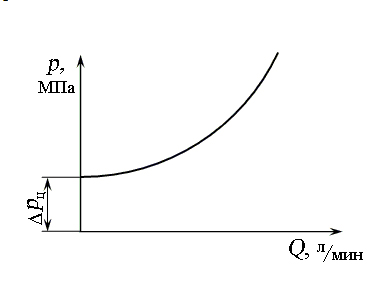
Рис. 8. Характеристика простого трубопровода с гидродвигателем

Если графически характеристика отображается в виде параболы, то есть существует квадратичная зависимость , график строится не менее чем по пяти точкам, первая из которых при Q = 0.

Если зависимость линейная, то есть , то достаточно выбрать две точки.