1. Пряма задача

Z = 14x₁+9x₂+8x₃+12x₄

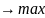
4 x₁+2x₂+x₃+4x₄≤528

2x₁+…+2x₃+3x₄≤228

2x₁+3x₂+x₃ +….≤568

2. Двоїста задача

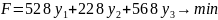
4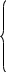 y₁+2y₂+2y₃ 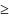14

2y₁+… + 3y₃ 9

y₁+2y₂+y₃ 8

4y₁+3y₂+… 12

2. Знаходження оптимального рішення прямої і двоїстої задач.

Вирішимо пряму задачу лінійного програмування симплексним методом, з використанням симплексного таблиці.

Визначимо максимальне значення цільової функції F (X) = 14x₁+9x₂+8x₃+12x₄ за таких умов-обмежень.

4x₁+2x₂+x₃+4x₄≤0528

2x₁+2x₃+3x₄≤0228

2x₁+3x₂+x₃≤0568

Для побудови першого опорного плану систему нерівностей наведемо до системи рівнянь шляхом введення додаткових змінних (перехід до канонічної форми).

В 1-м нерівності сенс (≤) вводимо базисну змінну x₅. В 2-м нерівності сенс (≤) вводимо базисну змінну x₆. В 3-м нерівності сенс (≤) вводимо базисну змінну x₇.

04x₁ + 02x₂ + 01x₃ + 04x₄ + 1x₅ + 0x₆ + 0x₇ = 0528

02x₁ + 0x₂ + 02x₃ + 03x₄ + 0x₅ + 1x₆ + 0x₇ = 0228

2x₁ + 03x₂ + 01x₃ + 0x₄ + 0x₅ + 0x₆ + 1x₇ = 0568

Матриця коефіцієнтів A = a(ij) цієї системи рівнянь має вигляд:

4	2	1	4	1	0	0
2	0	2	3	0	1	0
2	3	1	0	0	0	1

Вирішимо систему рівнянь відносно базисних змінних:

x₅, x₆, x₇,

Вважаючи, що вільні змінні рівні 0, отримаємо перші опорний план:

X1 = (0,0,0,0,0528,0228,0568)

Базис	В	x1	x2	x3	x4	x5	x6	x7
x5	528	4	2	1	4	1	0	0
x6	228	2	0	2	3	0	1	0
x7	568	2	3	1	0	0	0	1
F(X0)	0	-14	-9	-8	-12	0	0	0

Переходимо до основного алгоритму симплекс-методу.

Ітерація №0.

Поточний опорний план неоптімален, так що в індексному рядку знаходяться негативні коефіцієнти.

В якості ведучого виберемо стовпець, відповідний змінноїx₁, так як це найбільший коефіцієнт по модулю.

Обчислимо значення D_i по рядках як частка від ділення: b_i / a_i1

і з них виберемо найменше:

Отже, 2-ий рядок є провідною.

Дозволяє елемент дорівнює (2) і стоїть на перетині ведучого шпальти і головною рядки.

Базис	В	x1	x2	x3	x4	x5	x6	x7	min
x5	528	4	2	1	4	1	0	0	132
x6	228	2	0	2	3	0	1	0	114
x7	568	2	3	1	0	0	0	1	284
F(X1)	0	-14	-9	-8	-12	0	0	0	0

Після перетворень одержуємо нову таблицю:

Базис	В	x1	x2	x3	x4	x5	x6	x7
x5	72	0	2	-3	-2	1	-2	0
x1	114	1	0	1	1.5	0	0.5	0
x7	340	0	3	-1	-3	0	-1	1
F(X1)	1596	0	-9	6	9	0	7	0

Ітерація №1.

Поточний опорний план неоптімален, так що в індексному рядку знаходяться негативні коефіцієнти.

В якості ведучого виберемо стовпець, відповідний змінноїx₂, так як це найбільший коефіцієнт по модулю.

Обчислимо значення D_i по рядках як частка від ділення: b_i / a_i2

і з них виберемо найменше:

Отже, 1-ий рядок є провідною.

Дозволяє елемент дорівнює (2) і стоїть на перетині ведучого шпальти і головною рядки.

Базис	В	x1	x2	x3	x4	x5	x6	x7	min
x5	72	0	2	-3	-2	1	-2	0	36
x1	114	1	0	1	1.5	0	0.5	0	-
x7	340	0	3	-1	-3	0	-1	1	113.33
F(X2)	1596	0	-9	6	9	0	7	0	0

Після перетворень одержуємо нову таблицю:

Базис	В	x1	x2	x3	x4	x5	x6	x7
x2	36	0	1	-1.5	-1	0.5	-1	0
x1	114	1	0	1	1.5	0	0.5	0
x7	232	0	0	3.5	0	-1.5	2	1
F(X2)	1920	0	0	-7.5	0	4.5	-2	0

Ітерація №2.

Поточний опорний план неоптімален, так що в індексному рядку знаходяться негативні коефіцієнти.

В якості ведучого виберемо стовпець, відповідний змінноїx₃, так як це найбільший коефіцієнт по модулю.

Обчислимо значення D_i по рядках як частка від ділення: b_i / a_i3

і з них виберемо найменше:

Отже, 3-ий рядок є провідною.

Дозволяє елемент дорівнює (3.5) і стоїть на перетині ведучого шпальти і головною рядки.

Базис	В	x1	x2	x3	x4	x5	x6	x7	min
x2	36	0	1	-1.5	-1	0.5	-1	0	-
x1	114	1	0	1	1.5	0	0.5	0	114
x7	232	0	0	3.5	0	-1.5	2	1	66.29
F(X3)	1920	0	0	-7.5	0	4.5	-2	0	0

Після перетворень одержуємо нову таблицю:

Базис	В	x1	x2	x3	x4	x5	x6	x7
x2	135.43	0	1	0	-1	-0.14	-0.14	0.43
x1	47.71	1	0	0	1.5	0.43	-0.0714	-0.29
x3	66.29	0	0	1	0	-0.43	0.57	0.29
F(X3)	2417.14	0	0	0	0	1.29	2.29	2.14

Кінець ітерацій: індексний рядок не містить негативних елементів - знайдений оптимальний план

Остаточний варіант симплекс-таблиці:

Базис	В	x1	x2	x3	x4	x5	x6	x7
x2	135.43	0	1	0	-1	-0.14	-0.14	0.43
x1	47.71	1	0	0	1.5	0.43	-0.0714	-0.29
x3	66.29	0	0	1	0	-0.43	0.57	0.29
F(X4)	2417.14	0	0	0	0	1.29	2.29	2.14

Оптимальний план можна записати так:

x₂ = 135.43

x₁ = 47.71

x₃ = 66.29

F(X) = 014*47.71 + 09*135.43 + 08*66.29 = 2417.14

З останньої симплексної таблиці нескладно знайти оптимальний план і двоїстої задачі. Він матиме вигляд:

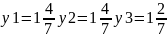
При цьому F min = 524*y1+224*y2+564*y3=1900.57

Легко побачити що Z max = F min = 1900.57

Економічний аналіз оптимальних планів прямої і двоїстої задач наступний.

Оптимальний план прямої задачі передбачає виробництво лише трьох видів продукції A, B, C у кількості виробництва A=47.43 (ум.од), B=134.86 (ум.од), C=64.57 (ум.од). Випуск продукції D(x4=0) не передбачається.

За такого оптимально плану виробництво продукції та використання ресурсів підприємство отримає найбільший дохід у розмірі 1900.57 умовних одиниць.

План двоїстої задачі дає оптимальну систему оцінок ресурсів, що використовуються у виробництві. Так з того, що 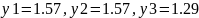(значення більші нуля), випливає, що ресурси 1-го, 2-го і 3-го видів ресурсу використовуються повністю. Ці висновки аналогічні отриманим на основі попереднього аналізу додаткових змінних оптимального плану прямої задачі.

Статус ресурсів прямої задачі можна визначити так:

Перший спосіб – підстановкою. Якщо обмеження виконується як рівняння, то відповідний ресурс дефіцитний, інакше – недефіцитний

Для розглядуваного прикладу матимемо:

4*47.43+2*134.86 +1*64.57 +4*0=524(524) (ресурс A дефіцитний)

2*47.43+0*134.86 +2*64.57 +4*0=224(224) (ресурс B дефіцитний)

2*47.43+3*134.86 +1*64.57 +0*0=564(564) (ресурс C дефіцитний)

Другий спосіб – за допомогою двоїстих оцінок. Якщо у не дорівнює 0, то ресурс дефіцитний, якщо ж у=0, то ресурс недефіцитний.

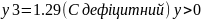
Визначаємо далі інтервали стійкості двоїстих оцінок відносно зміни запасів дефіцитних ресурсів.

Якщо запас першого дефіцитного ресурсу збільшити на одну умовну одиницю (b1=524+1=525), то цільова функція Z max збільшиться на 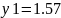ум.од. і становитиме Z max=1902.14.

Отже збільшення запасу першого дефіцитного ресурсу за інших умов приводить до падіння виробництва продукції х2 з 134.86 ум.од. до 134.71 ум. од., продукції х1 зросте від 47.43 ум.од до 47.86, а продукції С від 64.57 ум.од до 64.14 ум.од.

Якщо запас другого дефіцитного ресурсу збільшити на одну умовну одиницю (b2=224+1=225), то цільова функція Z max збільшиться на 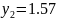ум.од. і становитиме Z max=1902.14.

Отже збільшення запасу другого дефіцитного ресурсу за інших умов приводить до падіння виробництва продукції х2 з 134.86 ум.од. до 134.71 ум. од., продукції х1 впаде від 47.43 ум.од до 47.36, а продукції С зросте від 64.57 ум.од до 65.14 ум.од.

Якщо запас третього дефіцитного ресурсу збільшити на одну умовну одиницю (b3=564+1=565), то цільова функція Z max збільшиться на 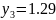ум.од. і становитиме Z max= 1901.86.

Отже збільшення запасу третього дефіцитного ресурсу за інших умов приводить до зростання виробництва продукції х2 з 134.86 ум.од. до 135.29 ум. од., продукції х1 впаде від 47.43 ум.од до  47.14, а продукції С зросте від 64.57 ум.од до 64.86 ум.од.

Після проведення аналізу постає логічне запитання, чи збережуться встановлені пропорції, якщо запас дефіцитного ресурсу змінити не на одиницю, а на 10 умовних одиниць. Щоб відповісти необхідно розрахувати інтервали можливої зміни обсягів дефіцитних ресурсів, у межах яких двоїсті оцінки (у) залишаються на рівні оптимальних значень

Приріст (зміну) запасу ресурсу 1 позначимо через ∆b1. Тоді якщо 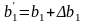то новий оптимальний план буде таким

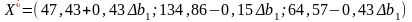
Єдина вимога, що можна поставити, до можливих нових оптимальних значень - це умова невід’емності тобто:

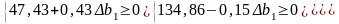
Це означає, що коли запас ресурсу 1 збільшиться на 150,2 умовні одиниці або зменшиться на 150,2 умовні одиниці, то оптимальною двоїстою оцінкою ресурсу 1 залишиться 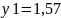. Отже, запас ресурсу 1 може змінюватись у межах:

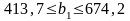
Згідно з цим максимально можливий дохід підприємства перебуватиме в межах:

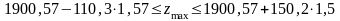
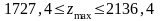
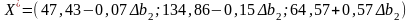
Аналогічно розраховуємо інтервал стійкості двоїстої оцінки для у2 та у3

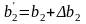
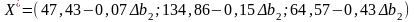
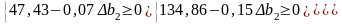
Отже, якщо запас ресурсу 2 може збільшиться на 677,6 ум.од або зменшиться на 113,3мум.од, то оптимальною двоїстою оцінкою ресурсу 2 залишиться 1,57.

Отже запас ресурсу 2 може змінюватись у межах:

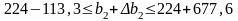
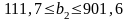
Згідно з цим максимально можливий дохід підприємства перебуватиме в межах:

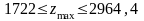
Приріст (зміну) запасу ресурсу 3 позначимо через ∆b3. Тоді якщо 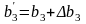то новий оптимальний план буде таким

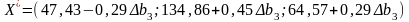
Єдина вимога, що можна поставити, до можливих нових оптимальних значень - це умова невід’емності тобто:

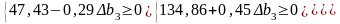
Це означає, що коли запис ресурсу 3 збільшиться на 163,6 умовні одиниці або зменшиться на 222,7 умовні одиниці, то оптимальною двоїстою оцінкою ресурсу 3 залишиться 1,29. Отже, запас ресурсу 3 може змінюватись у межах:

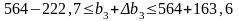
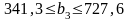
Згідно з цим максимально можливий дохід підприємства перебуватиме в межах:

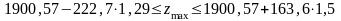
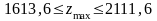
Визначені інтервали мають місце лише в тих випадках, коли змінюється тільки один ресурс, а запаси всіх інших фіксовані, тобто за інших однакових умов. У разі одночасної зміни обсягів усіх або кількох ресурсів підхід до визначення нового оптимального плану буде інший.

З 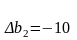мінимо обсяги всіх 3х ресурсів наступним чином:

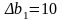
Матрицю можна отримати з останньої симплекс-таблиці. Вона має наступний вигляд:

Базис	В	x1	x2	x3	x4	x5	x6	x7
x2	143.14	0	1	0	-1.14	-0.14	-0.14	0.43
x1	46.57	1	0	0	1.43	0.43	-0.0714	-0.29
x3	61.43	0	0	1	0.57	-0.43	0.57	0.29
F(X4)	1929.43	0	0	0	2.57	1.57	1.57	1.29

Новий оптимальній план буде таким:

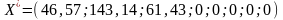
Усі 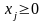і тому оптимальний план двоїстої задачі залишиться колишнім

Загальний максимальний дохід підприємства зміниться на 28.86 і становитиме 1929.43

Оцінка рентабельності продукції, що виготовляється на підприємстві, виконується за допомогою двоїстих оцінок та обмежень двоїстой задачі, які характеризують кожний вид продукції.

Підставимо 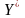у систему обмежень двоїстой задачі. Якщо вартість ресурсів на одиницю продукції(ліва частина) перевищує ціну цієї продукції(праву частину), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.

4*1,57+2*1,57+2*1,29=12=12 (продукція А рентабельна)

2*1,57+0*1,57+3*1,29=7=7 (продукція В рентабельна)

1*1,57+2*1,57+1*1,29=6=6 (продукція С рентабельна)

4*1,57+3*1,57+0*1,29=11>10 (продукція D нерентабельна)

Аналогічні результати можна дістати, проаналізувавши двоїсті оцінки додаткових змінних, значення яких показують, на скільки вартість ресурсів перевищує ціну одиниці відповідної продукції. Тому, якщо додаткова змінна двоїстої задачі дорівнює нулю, то продукція рентабельна.

Додаткові змінні двоїстої задачі розміщуються в оцінковому рядку останньої симплекс таблиці у стовпчиках. Їх оптимальні значення

у1=1,57 у2=1,57 у3=1,29 у4=0

Тому продукції А, В, С рентабельні, а продукція D нерентабельна.

Під впливом різних обставин ціна одиниці продукції на підприємстві може змінюватись(збільшуватись чи зменшуватись). І тому завжди важливо знати, у межах яких замін ціни продукції кожного виду оптимальний план її виробництва залишається незмінним, тобто для розглядуваного прикладу рівним

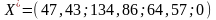
Для визначення інтервалів зміни коефіцієнтів цільової функції скористаємось тим, що при цьому симплекс-таблиця, яка відповідає оптимальному плану, зберігає свій вигляд за винятком елементів оцінкового ряду. Нові оцінки 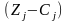мають задовольняти умову оптимальності задачі максимізації, тобто бути невід’ємними.

Зміну коефіцієнта 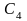позначимо через 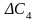. Оскільки х4 є небазисною змінною, то в симплекс-таблиці зміниться лише відповідна оцінка

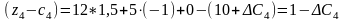
За умови 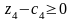дістанемо нерівність 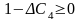тобто

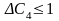
Це означає, що коли ціна одиниці продукції D за інших однакових умов зросте не більш ніж на 1 ум.од., то оптимальним планом виробництва продукції на підприємстві все одно залишиться . Лише максимальний дохід зміниться на

Складніше розраховуються інтервал зміни коефіцієнтів для базисного стовпчика. У цьому разі зміни відбуваються також у стовпчику 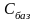симплекс-таблиці, а це у свою чергу стосується всіх ненульових оцінок ( ).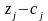

Так для базисної змінної 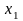зміна коефіцієнта на 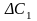приведе до таких оцінок:

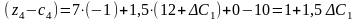
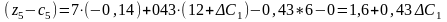
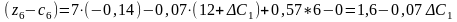
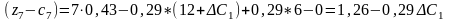
Нові значення оцінок мають задовольняти умову оптимальності, тобто 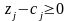. Тому інтервал для визначається з такої системи нерівностей:

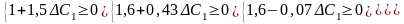
Отже ціна одиниці продукції С може змінюватись в межах

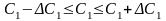, тобто

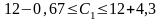
Звідси

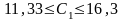
Таким чином, ціна одиниці продукції продукції С1 може збільшуватись на 4,3 та зменшуватись на 0,67 ум.од., і перебувати в межах від 11,33 до 16,3 ум.од.

Аналогічно для базисної змінної 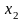зміна коефіцієнта на 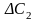приведе до таких оцінок:

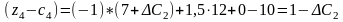
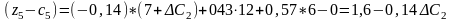
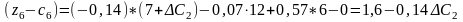
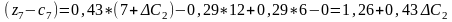
Нові значення оцінок мають задовольняти умову оптимальності, тобто . Тому інтервал для визначається з такої системи нерівностей:

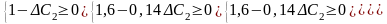
Отже ціна одиниці продукції С може змінюватись в межах

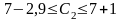
Звідси

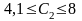
Таким чином, ціна одиниці продукції продукції С2 може збільшуватись на 1 та зменшуватись на 2,9 ум.од., і перебувати в межах від 4,1 до 8 ум.од.

Аналогічно для базисної змінної 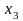зміна коефіцієнта на 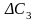приведе до таких оцінок:

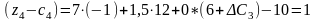
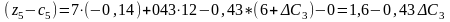
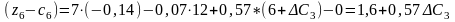
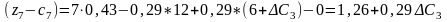
Нові значення оцінок мають задовольняти умову оптимальності, тобто . Тому інтервал для визначається з такої системи нерівностей:

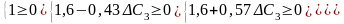
Отже ціна одиниці продукції С може змінюватись в межах

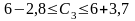
Звідси

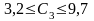
Таким чином, ціна одиниці продукції продукції С3 може збільшуватись на 3,7 та зменшуватись на 2,8 ум.од., і перебувати в межах від 3,2 до 9,7 ум.од.

Якщо коливання ціни продукції вийде за визначені межі, то план X вже не буде оптимальний і його необхідно буде поліпшувати згідно з алгоритмом симплекс-методу, тобто продовжить розв’язання задачі.

Проведений в даному прикладі аналіз лінійної моделі на чутливість дає широкий спектр динамічної інформації про визначений оптимальний план і змогу дослідити можливі зміни цього оптимального плану в результаті коректування умов прямої задачі.