2. Рішення задачі лінійного програмування в Excel.

Рішення ЗЛП в Excel виконується за допомогою блоку рішення Solver, який визивається за допомогою команди меню «Сервис-Поиск решения…»

Послідовність дій така:

1. Вводяться вхідні дані;

2. Вводяться залежності з математичної моделі

3. З меню «Сервис» відкривається діалогове вікно «Поиск решения…» в якому вводиться комірка цільової функції, її призначення (максимум чи мінімум), змінні комірки та добавляються обмеження.

4. В опції «Параметри» повинне бути помічене віконце «Лінійна модель».

Розглянемо рішення тієї ж задачі про ключки та шахові набори.

Введення вхідних даних показане на рис. 3.1

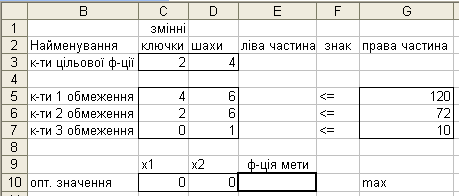
Рис.3.1.

Тепер необхідно ввести залежності з математичної моделі. Ці залежності містять у собі ліві частини обмежень і функцію мети (цільову функцію).

Вказану операцію можна виконати за допомогою функції СУММПРОИЗВ, для якої у якості першого аргументу вводяться коефіцієнти відповідного обмеження, а у другий масив – змінні х₁,х₂, точніше комірки де цим змінним задані початкові чисельні значення (на рис. 3.1. – комірки C10:D10). На рис.3.2 показано введення цієї функції для першого обмеження. Введення залежностей з математичної моделі для інших обмежень, а також для функції мети, виконується аналогічно у відповідних комірках таблиці. У якості першого масиву функції СУММПРОИЗВ для функції мети використовуються коефіцієнти цільової функції.

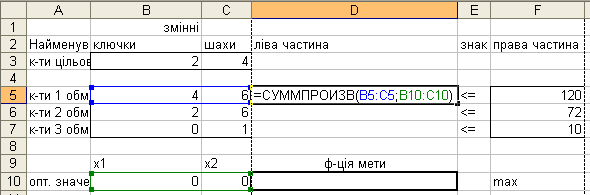
Рисунок. 3.2.

В меню «Сервіс» відчинемо вікно «Поиск решений…» (див. рис. 3.3).

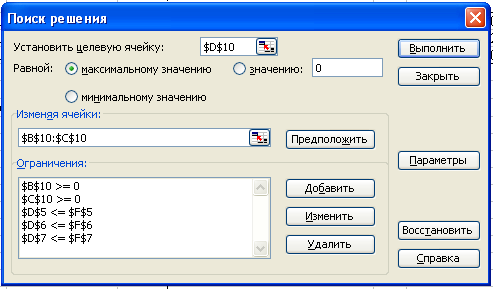
Рисунок 3.3.

У відчиненому вікні у полі «Установить целевую ячейку» введемо координати комірки, відведеної для функції мети, а саме $D$10.

У групі радіокнопок «Равной» виберемо «максимальному значению».

В полі області «Изменяя ячейки:» необхідно ввести координати комірок з початковими чиселиними значеннями змінних, а саме $В$10:$С$10.

Після цього вводяться обмеження. З цією метою необхідно натиснути кнопку «Добавить», в результаті чого відчиниться нове вікно «Добавление ограничения» (рис.3.4).

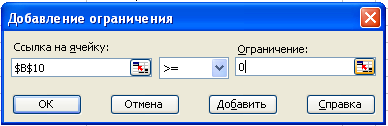
Рисунок 3.4.

Виористовуючи три поля і набор кнопок у цьомі вікні, вводяться всі обмеження, зображені у відповідному полі вікна «Поиск решения», зображеному на рис. 3.3. У нашій задачі всі ліві частини повинні бути менші або рівні правим частинам. Крім того, змінні моделі повинні бути більшими або рівними нулю.

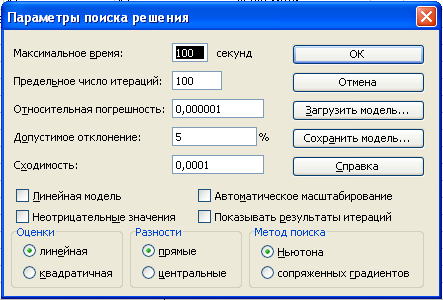
Рисунок 3.5.

Після того, як всі обмеження були успішно введені, шляхом натискання на кнопку «Параметрі» необхідно відчинити вікно «Параметрі поиска решений» (рис. 3.5). У полях вікна вже задані типові значення параметрів пошуку (дивись рис. 3.5), які за бажанням можна змінити. Оскільки нами вирішується лінійна задача, нам у цьому вікні необхідно виставити прапорець «Линейная модель». Після натискання кнопки «ОК» у цьому вікні знову з’явиться вікно «Поиск решения». Для отримання розв’язку задачі необхідно у вікні «Поиск решения» натиснути на кнопку «Выполнить», у результаті чого на екран виведеться вікно «Результаты поиска решения» (рис. 3.6).

Рисунок 3.6.

Якщо рішення не отримане, то у вікні з’явиться відповідне повідомлення. Якщо ж рішення отримане, то за допомогою цього вікна можна отримати три типи звітів (бажані для отримання звіти необхідно помітити у полі №Тип отчета» за допомогою миші).Кожен із звітів відкривається на відповідній сторінці робочої книжки Excel.

У звіті по результатах висвітлюються відомості про цільову функцію, про значення шуканих даних та результати оптимального рішення для обмежень. Для обмежень у колонці «Формула» показані залежності, які були введені у діалогове вікно «Поиск решения»; у колонці «Значение» показані значення використаного ресурсу; у колонці «Разница» показана кількість невикористаного ресурсу. Якщо ресурс використовується повністю, то у колонці «Статус» висвітлюється «связанное», в противному разі «не связан.».

У звіті «Устойчивость» поданий аналіз по змінних та обмеженнях.

В аналізі змінних висвітлені наступні результати:

• початкові та результуючі (оптимальні) значення змінних;

• нормована вартість, тобто додаткові двоїсті змінні, які показують, наскільки зміниться цільова функція при примусовому збільшенні на одиницю кількості даного виду продукції (втрати прибутку за рахунок неефективного використання ресурсів);

• коефіцієнти цільової функції;

• допустимі значення приросту коефіцієнтів цільової функції, при яких зберігаються значення змінних, що входять в оптимальне рішення.

В аналізі обмежень висвітлені значення:

• величини використаних ресурсів;

• тіньові ціни, тобто двоїсті оцінки, що показують, як зміниться цільова функція при зміні кількості цього ресурсу на одиницю.

• відповідні значення збільшення і зменшення ресурсів, при яких ще зберігається оптимальний набір змінних, що входять у оптимальне рішення.

• У звіті «Пределы» показано, у яких межах може змінюватись випуск продукції, що потрапила у оптимальне рішення при зберженні структури оптимального рішення.