МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ

ФЕДЕРАЦИИ

КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра алгебры, геометрии и методики преподавания математики

Кафедра математического анализа

УТВЕРЖДАЮ

Проректор по учебной работе

_____________ В.И. Васильев

« ___ » ______________ 2010 г.

__________________________

(дата дополнений и изменений)

___________________________

___________________________

ПРОГРАММА

ГОСУДАРСТВЕННОГО ЭКЗАМЕНА ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»

Направление 050000 – Образование и педагогика

Специальность 050202 – «Информатика» с дополнительной специальностью «Математика»

Факультет Математики и информационных технологий

Форма обучения очная

Курс 5

Семестр 10

Курган 2010

Программа составлена:

- с учетом требований Государственного образовательного стандарта высшего профессионального образования к минимуму содержания и уровню подготовки выпускников по специальности Информатика с дополнительной специальностью «Математика» 050202; № гос. регистрации 662 пед/СП. От 31.01.05 г.;

- в соответствии с учебным планом подготовки специалистов по специальности 050202 «Информатика» с дополнительной специальностью «Математика», утвержденного ученым советом университета 03.02.2006.

Программа утверждена на заседании кафедры алгебры, геометрии и методики преподавания математики «26» октября 2009 г. (протокол №2).

Заведующий кафедрой алгебры,

геометрии и методики преподавания

математики

канд. ф.-м. наук, ____________/О.Н. Шатных/

Заведующий кафедрой

математического анализа

доцент, канд. ф.-м. наук, __________/М.В. Гаврильчик/

Программу составили:

канд. ф.-м. наук, ____________/О.Н. Шатных/

доцент, канд. ф.-м. наук, __________/М.В. Гаврильчик/

Согласовано:

Декан факультета математики

и информационных технологий

канд. пед. наук, доцент ____________/А.Т. Зверева/

Инженер Центра качества __________/О.В. Шередекова/

Руководитель Центра качества

доцент, канд. т. наук __________/С.В. Хрипунов/

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Основной целью государственного экзамена по математике является выявление уровня математической культуры выпускников и их подготовленности к преподаванию математики в общеобразовательной школе.

В соответствии с Государственным образовательным стандартом высшего профессионального образования выпускник должен

- знать роль и место математики в системе наук; обосновать фундаментальный и прикладной характер математики;

- владеть системой основных математических структур и аксиоматическим методом;

- владеть методологией построения математических моделей (дискретных и непрерывных, вероятностных и детерминированных); знать конкретные математические модели в экономике, экологии, социологии, психологии;

- владеть конкретными численными методами решения задач на ЭВМ.

Основная задача государственного экзамена - закрепить теоретические знания и практические навыки по дисциплине специализации.

В соответствии с основной задачей государственного экзамена программа включает в себя основные и наиболее важные вопросы курсов «Математический анализ», «Алгебра и теория чисел» и «Геометрия», раскрывает содержание каждой темы, определяет требования к ответу студента на государственном экзамене по тому или иному вопросу.

Государственный экзамен по дисциплине «Математика» проводится в устной форме. Студент получает билет, состоящий из двух теоретических вопросов по разным курсам и одной задачи. На подготовку студенту отводиться не менее полутора часов.

Специалист должен свободно ориентироваться в основных разделах фундаментальных математических дисциплин, что включает:

- в области математического анализа — множество действительных чисел, функции одного переменного (предел, непрерывность, дифференциальное и интегральное исчисление, задачи на экстремум), числовые последовательности и ряды;

- в области алгебры и теории чисел — основные структуры современной алгебры (группы, кольца, поля), группы преобразований, комплексные числа и многочлены, матричную алгебру и решение систем линейных уравнений, линейные пространства;

• в области геометрии — векторы, линейную зависимость, скалярное, векторное и смешанное произведения векторов, уравнения прямой линии на плоскости, уравнения плоскости, линии второго порядка, аффинные и изометрические преобразования плоскости и пространства, плоские сечения, аффинную классификацию, изображение фигур при параллельном проектировании;

- в области дифференциальных уравнений — понятие дифференциального уравнения, элементарные приемы интегрирования, задачу Коши.

Оценку «неудовлетворительно» студент получает, если он не может сформулировать и доказать основные положения предлагаемой темы. Оценка «удовлетворительно» ставится в том случае, если студент ответил на 2/3 билета. Если при ответе студент сформулировал и доказал основные положения, но допустил вычислительные ошибки или не доказал вспомогательные утверждения, то ему ставится оценка «хорошо». В том случае, если студент сформулировал все основные определения, сформулировал и доказал основные и вспомогательные предложения и правильно решил задачу он получает оценку «отлично».

В программе приведен список обязательной литературы, которая должна быть изучена выпускниками при подготовке к государственному экзамену.

Содержание программы

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

I. Аксиоматическое построение теории действительных чисел.

1. Множество рациональных чисел Q.

2. Необходимость расширения Q. Доказать теорему: не существует

рационального числа, квадрат которого равен двум.

3. Аксиоматическое определение R.

II.Отображения множеств (функции).

1. Понятие отображения одного множества в другое. Примеры отображений.

2. Определение числовой функции. Область определения функции, множество значений. Примеры. График функции.

3. Классификация функций по аналитическим выражениям: а)целые рациональные, дробно-рациональные, иррациональные, алгебраические, трансцендентные; б) элементарные и неэлементарные.

4. Классификация функций по свойствам: ограниченность, четность, периодичность, монотонность.

Литература: [1], [2], [9], [13], [14].

III. Предел числовой последовательности. Число е.

1. Определение последовательности. Обозначение. Примеры: арифметическая и геометрическая прогрессии.

2. Определение предела последовательности.

3. Ограниченные и неограниченные последовательности, монотонные последовательности. Примеры.

4. Теорема о пределе монотонной последовательности. Примеры применения: число е, длина окружности, площадь круга.

Литература: [1], [2], [9], [13], [14].

IV. Предел функции в точке.

1. Понятие предельной точки множества. Определение предела

функции в точке на “языке последовательностей”, на “языке ε - δ”.

2. Теоремы о пределах суммы, произведения и частного функций,

имеющих пределы.

Литература: [1], [2], [9], [13], [14].

V. Непрерывность функции в точке. Основные свойства функций, непрерывных на отрезке.

1. Определение непрерывности функции в точке. Примеры непрерывных функций.

2. Теоремы о непрерывности в точке суммы, произведения и частного функций, непрерывных в точке.

3. Определение непрерывности функции на множестве. Теоремы:

- об ограниченности функции, непрерывной на отрезке;

• о достижении функцией, непрерывной на отрезке, верхней и нижней граней;

• об обращении функции в нуль;

• о промежуточных значениях функции, непрерывной на отрезке.

4. Применение теорем об обращении функции в нуль и о промежуточных значениях к решению уравнений и неравенств, для приближенного вычисления корней уравнений.

Литература: [1], [2], [9], [13], [14].

VI. Дифференцируемые функции одной переменной. Геометрический и механический смысл производной. Правила дифференцирования.

1. Задачи, приводящие к понятию производной. Определение производной функции в точке. Примеры. Геометрический и механический смысл понятия производной функции в точке.

2. Определение дифференцируемости функции в точке. Необходимое и достаточное условие дифференцируемости функции в точке (доказать). Связь непрерывности и дифференцируемости функции в точке (обосновать).

3. Производная суммы, произведения и частного функций, имеющих производные (доказать любую по выбору).

Литература: [3], [9], [13], [14].

VII. Условия постоянства и монотонности функции на промежутке. Экстремумы функции.

1. Теорема Лагранжа.

2. Необходимое и достаточное условие постоянства функции (доказать).

3. Монотонные функции. Достаточное условие строгой монотонности функции на промежутке. Примеры.

4. Понятие экстремума функции. Необходимые условия экстремума. Достаточные условия экстремума функции (доказать одно из них). Примеры.

Литература: [3], [9], [13], [14].

VIII. Первообразная и неопределенный интеграл. Интегрирование подстановкой и по частям.

1. Определение первообразной функции. Примеры.

2. Неопределенный интеграл, геометрический смысл неопределенного интеграла, свойства неопределенного интеграла (доказать). Таблица интегралов.

3. Интегрирование по частям и заменой переменной (с выводом). Примеры.

Литература: [4], [9], [13], [14].

IX. Определенный интеграл. Интегрируемость непрерывной функции. Формула Ньютона-Лейбница.

1. Задачи, приводящие к понятию определенного интеграла.

2. Определение и обозначение определенного интеграла. Геометрический смысл определенного интеграла.

3. Интеграл с переменным верхним пределом 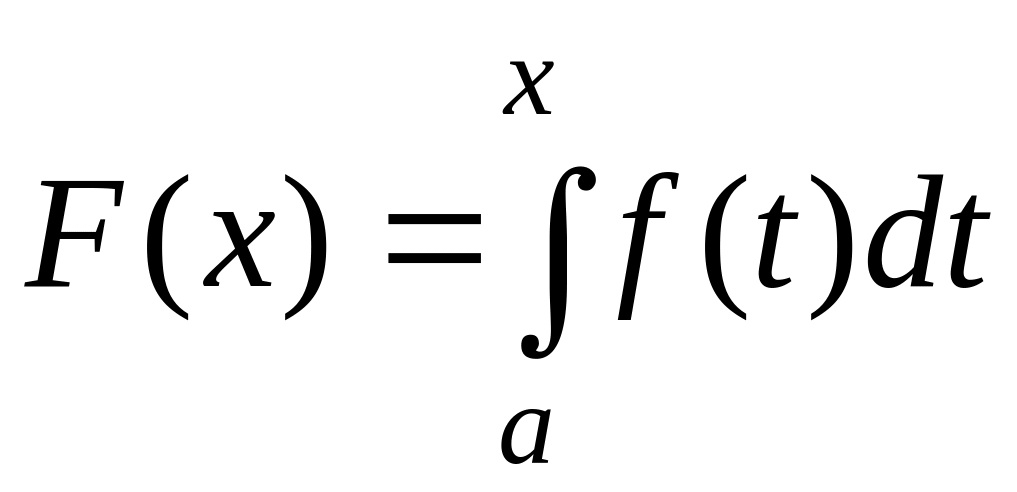Связь между неопределенным и определенным интегралами. Формула Ньютона-Лейбница; ее применение к вычислению определенных интегралов. Пример.

Литература: [4], [9], [13], [14].

X. Понятие площади плоской фигуры. Приложение определенного интеграла к вычислению площади плоской фигуры.

1. Определение квадрируемой фигуры.

2. Доказать квадрируемость криволинейной трапеции, вывести формулу для вычисления ее площади.

Литература: [4], [9], [13], [14].

XI. Приложения определенного интеграла к вычислению объема тела.

1. Кубируемые тела. Формулы для вычисления объема тела по площадям параллельных сечений и объема тела вращения.

2. Вычислить объем цилиндра, шара, конуса, усеченного конуса, пирамиды.

3. Определение спрямляемой кривой, определение длины дуги кривой.

4. Длина дуги окружности.

Литература: [4], [9], [13], [14].

XII. Числовые ряды. Признаки сходимости рядов с положительными членами. Знакопеременные ряды.

1. Понятие числового ряда. Частичная сумма ряда. Сумма ряда. Сходящиеся и расходящиеся ряды. Геометрический ряд. Необходимое условие сходимости ряда (доказать).

2. Достаточные признаки сходимости положительных рядов: признаки сравнения, Даламбера и Коши.

3. Знакопеременные и знакочередующиеся ряды. Теорема Лейбница о сходимости знакочередующегося ряда. Применение теоремы Лейбница для приближенного вычисления сумм рядов.

Литература: [5], [9], [13], [14].