3.Этап реализации

На этом этапе идет описание компонентов, использованных для осуществления связи приложения с базой, их свойств и методов.

Рассмотрим таблицу 1, в которой расписаны используемые компоненты, их свойства и методы и их назначение.

Таблица1

Компонент, свойства	Назначение
AdoConnection	Используется для указания базы данных и работы с транзакциями.
Свойства:
Connectionstring: string;	Задает параметры соединения с БД.
Connected: Boolean;	True - соединение с ADO-источником.
AdoTable	Таблица ADO, обеспечивает доступ к одной таблице ADO–источника.
Свойства:
Connection:TAdoConnection;	Служит для указания соответствующего компонента AdoConnection.
Tablename: string;	Имя таблицы ADO–источника, с которой связан НД.
Active: Boolean;	True – НД открыт.
Методы:
Open;	Аналогично значению true в свойстве active.
Close;	Аналогично значению false в свойстве active.
First;	Установление маркера НД на первую запись.
Next;	Установление маркера НД на следующую запись.
Prior;	Установление маркера НД на предыдущую запись.
Last;	Установление маркера НД на последнюю запись.
Delete;	Удаляет текущую запись.
DataSource	Источник данных, является промежуточным звеном между НД и визуальными компонентами.
Dataset: T DataSet;	Служит для указания НД, с которым связан источник данных.
DBGrid	Используется для отображения содержимого НД в виде таблицы.
DataSource: TDataSource;	Служит для указания источника данных, через который компонент связан с НД.
TAdoQuery	Запрос ADO, позволяет выполнять SQL-команды для получения данных из ADO-источника.
Свойства:
Connection:TAdoConnection;	Служит для указания соответствующего компонента AdoConnection.
Active: Boolean;	True – НД открыт.
SQL: TStrings;	Содержит текст SQL-команды.
Методы:
Open;	Аналогично значению true в свойстве active.
Close;	Аналогично значению false в свойстве active.

Еще раз напомним, что это перечень используемых при создании приложения свойств и методов, на самом деле их гораздо больше. Следует отметить, еще одно свойство у компонента TAdoTable и TAdoQuery, которое не перечислено, но часто используется в приложении.Это свойство Fieldbyname(<имя поля>), позволяющее организовать доступ к полю, имя которого указано как аргумент. Для доступа к значению поля служат свойства value и AsXXX. Свойство value типа variant представляет собой фактические данные в объекте TField. При выполнении приложения это свойство используется для чтения и записи в поле. Если программист обращается к свойству value, то он должен самостоятельно обеспечивать преобразование и согласование типов значений полей и читаемых или записываемых значений.

20. Алгоритмы. Алгоритмизация. Понятие алгоритма. Различные подходы к формированию понятия «алгоритм». Свойства алгоритмов. Исполнитель алгоритмов. Различные способы записи алгоритмов. Алгоритмы: линейные, разветвляющиеся, циклические алгоритмы. Циклы. Виды циклов. Подпрограммы. Итерация и рекурсия. Примеры.

Слово «алгоритм» происходит из Средней Азии. В VI в. до н.э. в низовьях Амударьи возникло государство Хорезм, просуществовавшее до 712 г. н. э. В этот год его завоевали арабы, позже оно вошло в состав Монгольской империи. В математике Хорезм известен тем, что там жил Абу-Джафар Мухаммед ибн Муса (787-ок.850 г.), написавший трактат «Китаб аль-джебр валь-мукабала» («Книга о восстановлении и противопоставлении»). Его работы были переведены на латинский язык в XII в. и оказали большое влияние на развитие математики в Западной Европе. Имя и работы Абу-Джафара Мухаммеда ибн Мусы аль-Хорезми (буквально: из Хорезма) внесли в математику два слова: «алгоритм» и «алгебра».

Математическая энциклопедия (М.: Советская энциклопедия, 1977) так определяет понятие алгоритма:

алгоритм - точное предписание, которое задает вычислительный процесс (называемый в этом случае алгоритмическим), начинающийся с произвольного исходного данного (из некоторой совокупности возможных для данного алгоритма исходных данных) и направленный на получение полностью определяемого этим исходным данным результата.

Академик А.И.Мальцев (Алгоритмы и рекурсивные функции. М.: Наука, 1986) уточняет понятие процесса:

алгоритм - это процесс последовательного построения величин, идущий в дискретном времени таким образом, что в начальный момент задается исходная конечная система величин, а в каждый следующий момент система величин получается по определенному закону из системы величин, имевшихся в предыдущий момент времени.

Профессор Стэнфордского университета Д.Кнут (Калифорния, США) в книге «Искусство программирования для ЭВМ» (Т. 1) отмечает, что современное значение слова «алгоритм» очень схоже со значением слов «рецепт», «процесс», «метод», «способ», «процедура», «программа», но имеет свой дополнительный смысловой оттенок.

Прежде всего отметим, что алгоритм - это предписание. Предписание должно быть задано (закодировано) в некоторой форме. Это может быть текст - строка символов в некотором алфавите, таблица, диаграмма, упорядоченный набор пиктограмм и т.д.

Алгоритмизация – это процесс построения алгоритма решения задачи, результатом которого является выделение этапов процесса обработки данных, формальная запись содержания этих этапов и определение порядка их выполнения.

Свойства алгоритмов:

- Дискретность.

- Элементарность шагов.

- Определенность (детерминированность).

- Конечность (финитность).

- Массовость.

Дискретность означает, что алгоритм состоит из конечного числа описаний шагов и эти шаги выполняются в дискретном времени, т. е. любые два последовательных шага разделены при исполнении конечным, ненулевым отрезком времени. Можно считать, что шаги выполняются мгновенно в моменты времени t0, t1, t2, ... -, а между этими моментами ничего не происходит.

Элементарность шагов означает, что объем работы, выполняемой на любом шаге, мажорируется некоторой константой, зависящей от характеристик исполнителя алгоритмов, но не зависящей от входных данных и промежуточных значений, получаемых алгоритмом. Для численных алгоритмов такими элементарными шагами могут быть, например, сложение, вычитание, умножение, деление, сравнение двух 32-разрядных чисел, пересылка одного числа из некоторого места памяти в другое. К элементарным шагам не относится сравнение двух файлов, так как время сравнения зависит от длины файлов, а длина потенциально неограниченна.

Определенность (детерминированность) алгоритма означает, что для каждого шага могут быть по набору исходных для этого шага данных однозначно вычислены результаты выполнения шага, и эти результаты не зависят ни от каких случайных факторов. Соответственно этому и алгоритм в целом по окончании работы исполнителя выдает вполне определенный результат.

Конечность (финитность) алгоритма означает, что для получения результата нужно выполнить конечное число шагов, т. е. исполнитель в некоторый момент времени останавливается. Требуемое число шагов зависит от входных данных алгоритма и не мажорируется константой.

Массовость означает, что входные данные для алгоритма могут выбираться из некоторого множества значений. Если же входные данные уникальны, то алгоритм в силу свойства определенности (детерминированности) будет давать всегда один и тот же результат и само построение алгоритма теряет смысл.

Исполнитель и разработчик алгоритма

Разрабатывать, придумывать алгоритмы могут только разумные существа (например, человек). А вот формально (не думая и не оценивая) исполнять, могут какие-либо машины (например, компьютеры, бытовые приборы). В чем польза такого разделения труда? Дело в том, что человек освобождается от рутинной деятельности, которая часто может занимать много времени, и поручает ее машинам.

Понятие исполнителя невозможно определить с помощью какой-либо формализации. Исполнителем может быть человек, группа людей, робот, станок, компьютер, язык программирования и т.д. Важнейшим свойством, характеризующим любого из этих исполнителей, является то, что исполнитель умеет выполнять некоторые команды. Так исполнитель-человек умеет выполнять такие команды, как «встать», «сесть», «включить компьютер» и т.д., а исполнитель - язык программирования Бейсик - команды PRINT, END, LIST и другие аналогичные. Вся совокупность команд, которые данный исполнитель умеет выполнять, называется системой команд исполнителя (СКИ).

Однако машины не люди: приборы понимают лишь ограниченное число команд и могут обрабатывать данные (объекты) далеко не всех типов. Отсюда следует, что разработчик алгоритма в конечном итоге должен описать алгоритм в допустимых командах определенного исполнителя (той машины, которой будет поручено выполнение алгоритма). Совокупность команд, которые данный исполнитель может выполнять, называется системой команд исполнителя. Объекты (данные), над которыми исполнитель может выполнять действия, формируют среду исполнителя.

Различные способы записи алгоритмов

Алгоритм, составленный для некоторого исполнителя, можно представить различными способами: с помощью графического или словесного описания, в виде таблицы, последовательностью формул, записанным на алгоритмическом языке (языке программирования). Остановимся на графическом описании алгоритма, называемом блок-схемой. Этот способ имеет ряд преимуществ благодаря наглядности, обеспечивающей, в частности, высокую "читаемость" алгоритма и явное отображение управления в нем.

Язык блок-схем

Алгоритм можно описать разными способами: словами, на языке программирования, а также с помощью блок-схем.

На языке блок-схем каждый шаг алгоритма описывается с помощью соответствующей фигуры, а последовательность выполнения шагов определяется линиями-связями. Блок схемы читаются сверху вниз и слева направо.

Блок-схемы полезны тем, что обеспечивают легкую «читаемость» алгоритма. Однако это не всегда так: стоит попытаться нарисовать блок-схему для более-менее сложного алгоритма, как она разрастается до невероятных размеров и теряет все свое наглядное преимущество. Поэтому блок-схемы хороши в структурном программировании для описания коротких алгоритмов.

Язык блок-схем прост (хотя существуют его расширенные варианты):

Овал – начало и конец алгоритм

Прямоугольник – выполнение действия (например, c = a + b)

Ромб – проверка условия (например, a > b). Если условие выполняется, то алгоритм идет по линии «да», если не выполняется – то по линии «нет».

Скругленный прямоугольник – начало и конец алгоритма

Скошенный прямоугольник – ввод-вывод данных (например, получение значения переменной, вывод результата на экран монитора).

Алгоритмы:

Линейный алгоритм - это такой, в котором все операции выполняются последовательно одна за другой (например, вычисление периметра прямоугольника).

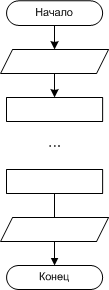
(пример)

Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие.

Ветвление if

Это самый простой тип ветвления. Если результат вычисления выражения-условия возвращает true (правда), то выполнение алгоритма идет по ветке «Да», в которую включены дополнительные выражения-действия. Если условие возвращает false (ложь), то выполнение алгоритма идет по ветке «нет», т.е продолжает выполняться основная ветка программы.

Ветвление if-else

Если выражение-условие возвращает true (правда), то выполнение алгоритма идет по ветке «Да», если условие не выполняется (false), то выполнение идет по ветке «Нет». При любом результате выражения-условия нельзя вернуться в основную ветку программы, минуя дополнительные действия.

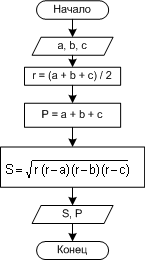
Например, решение квадратного уравнения:

Циклические алгоритмы.

Цикл while

Пока условие выполняется (результат логического выражения дает true), будут выполняться действия тела цикла. После очередного выполнения вложенных действий условие снова проверяется. Для того чтобы выполнение алгоритма не зациклилось, в теле цикла (помимо прочих действий) должно быть выражение, в результате выполнения которого будет изменяться переменная, используемая в условии. Тело цикла может ни разу не выполнится, если условие с самого начала давало false.

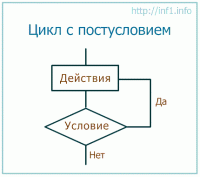
Цикл do

В этом цикле первый раз условие проверяется лишь после выполнения действий тела цикла. Если условие возвращает true, то выражения-действия повторяются снова. Каким бы ни было условие, тело данного цикла хотя бы раз, но выполнится.

Цикл for

Данный цикл также называют циклом «Для» (for). В его заголовке указывается три параметра: начальное значение переменной (от), конечно значение (до) и ее изменение с помощью арифметической операции на каждом «обороте» цикла (шаг).

Подпрограммы.

Если какая-нибудь часть программы повторяется многократно, то её оформляют отдельно от основной программы и называют подпрограммой.

Итерация. Рекурсия.