Пример вычисления и статистической оценки существенности параметров парной линейной корреляции

Пусть необходимо оценить взаимосвязь между линейной плотностью нитей и разрывной нагрузкой по основе пальтовых тканей, показатели которых представлены в табл. 6.1. [3]

Таблица 6.1

Показатели структуры и свойств пальтовых тканей

№ измерения	1	2	3	4	5	6	7	8	9	10
Линейная плотность, текс	11.5	26	18.8	22.5	12.8	13.6	18.7	21.8	15	15.2
Разрывная нагрузка, Н	507	660	425	558	538	388	580	570	413	506

Чтобы предварительно определить наличие такой связи, необходимо построить график точек, соответствующих сочетанию показателей свойств – корреляционное поле точек (рис. 6.2). По тесноте группирования точек можно судить о наличии корреляционной связи. Если нанести на корреляционном поле средние значения , то проведенная линия будет являться линией регрессии. На рисунке видна определённая связь между переменными и , которая характеризуется линейной зависимостью.

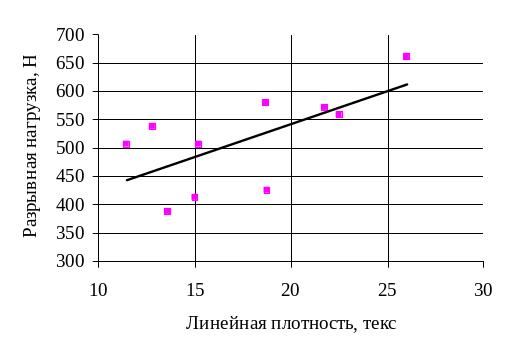
Рис. 6.2. Корреляционное поле точек

Критерием близости корреляционной зависимости и к линейной функциональной зависимости является коэффициент корреляции , показывающий степень тесноты связи между и .

Коэффициент корреляции рассчитываем по формуле (6.1).

.

Для упрощения промежуточных вычислений и расчета коэффициента используем табл. 6.2.

Таблица 6.2

Расчеты для определения коэффициента корреляции

№ п/п
1	11,5	507	5830,5	132,25	257049
2	26	660	17160	676	435600
3	18,8	425	7990	353,44	180625
4	22,5	558	12555	506,25	311364
5	12,8	538	6886,4	163,84	289444
6	13,6	388	5276,8	184,96	150544
7	18,7	580	10846	349,69	336400
8	21,8	570	12426	475,24	324900
9	15	413	6195	225	170569
10	15,2	506	7691,2	231,04	256036
	175,9	5145	92856,9	3297,71	2712531

Для контроля существования корреляционной зависимости рассчитываем критерий Стьюдента по формуле (6.2).

.

Полученное значение больше табличного значения (прил. 2) при числе степеней свободы равном и доверительной вероятности 0.95, что свидетельствует о существовании корреляционной зависимости между рассматриваемыми параметрами.

Значение коэффициента корреляции , при значении критерия , свидетельствует о том, что связь между рассмотренными свойствами тканей является удовлетворительной. Очевидно, это объясняется тем, что на прочность ткани влияет не только линейная плотность нитей, но и их количество, однако толщина нитей имеет существенное значение.