4.3. Расчет реализованного плана пфэ

Расчет реализованного плана ПФЭ заключается в определении коэффициентов уравнения регрессии, значимости этих коэффициентов и установлении адекватности уравнения (соответствия принятой математической модели процесса экспериментальным данным).

Уравнение адекватно описывает результаты опытов, если квадратические отклонения значений выходного параметра (рассчитанных по уравнению регрессии) от экспериментальных данных обусловлены только погрешностью воспроизводимости (т. е. точности воспроизведения результатов опыта при его повторении в одинаковых условиях).

Последовательность вычислений при обработке результатов исследований рассмотрим на примере реализации матрицы планирования, табл. 4.2. Полагаем, что в результате проведения опытов были получены данные, сведенные в табл. 4.5.

Значения y₁, y₂ в табл. 4.5 представляют собой экспериментальные данные повторных (дублированных) опытов. Для расчёта дисперсии воспроизводимости в эксперименте проводилось равномерное дублирование наблюдений ( ).

Таблица 4.5

Матрица планирования и значения опытных данных

Ν	x1	x2	x3	Параметр оптимизации			Δ yj1	Δ yj2	(Δ yj1)2= (Δ yj2)2	Sj2
				y1	y2
1	–	–	–	80,23	81,93	81,08	-0,85	0,85	0,723	1,446
2	+	–	–	86,50	84,80	85,65	0,85	-0,85	0,723	1,446
3	–	+	–	82,45	82,10	82,27	0,18	-0,18	0,032	0,064
4	+	+	–	89,50	91,30	90,40	-0,90	0,90	0,810	1,620
5	–	–	+	85,10	84,30	84,95	0,15	-0,15	0,023	0,046
6	+	–	+	90,30	89,60	89,95	0,35	-0,35	0,123	0,246
7	–	+	+	85,60	84,90	85,25	0,35	-0,35	0,123	0,246
8	+	+	+	88,02	88,48	88,25	-0,23	0,23	0,053	0,106
∑									2,610	5,220

Величина является средним арифметическим повторных опытов:

, (4.5)

где – номер параллельного опыта; – значение параметра оптимизации в -м параллельном опыте -й строки матрицы, п – число повторных опытов (в рассматриваемом случае, в табл. 4.4 п=2).

Рассчитаем средние значения параметра оптимизации для каждого опыта. Для первого опыта имеем:

и аналогично находим искомые значения для остальных опытов, помещая их в соответствующий столбец (табл. 4.5).

Далее находим , которые для первого опыта имеют величины:

;

Аналогично находим значения для остальных опытов и результаты заносим в соответствующие столбцы, как и величины ( у_j1)²=( у_j2)².

Первой задачей, стоящей перед исследователем после реализации плана, является оценка экспериментальных данных на воспроизводимость. С этой целью рассчитываются построчные дисперсии серий опытов по формуле

. (4.6)

В первом опыте имеем:

,

а остальные значения приведены в соответствующем столбце табл.3.5. Подсчитаем сумму этого столбца (она равна ) и выделим в нём максимальную дисперсию

Далее определяется сумма всех дисперсий , где – число опытов.

Зная сумму построчных дисперсий, можно оценить воспроизводимость опытов по критерию Кохрена :

(4.7)

При опыты воспроизводимы (статистически однородны). При необходимо принять при проведении исследования более точные методы и средства измерения.

Например, имеем

Здесь значение определено (см. прил. 5) при уровне значимости , числе степеней свободы и числе опытов

Так как значения критерия Кохрена по опытным данным не превосходят его критического значения, взятого из таблицы, может быть сделан вывод о достаточно хорошей воспроизводимости опытов. Если бы по расчету оказалось, что , опыт с максимальной дисперсией следовало бы исключить из рассмотрения или, в лучшем случае, повторить его с целью выяснения вопроса, случайным ли было отклонение.

Если дисперсии опытов однородны, то вычисляют дисперсию воспроизводимости эксперимента :

. (4.8)

Так как в рассматриваемом примере дисперсию воспроизводимости находим по формуле:

.

Уравнение регрессии ПФЭ 2³ имеет вид:

Если установлено, что опыты в точках плана воспроизводятся достаточно хорошо (ряд построчных дисперсий однороден), производится расчет коэффициентов уравнения регрессии:

свободный член

; (4.9)

коэффициенты регрессии, характеризующие линейные эффекты

; (4.10)

коэффициенты регрессии, характеризующие эффекты взаимодействия

, (4.11)

где – номера факторов; – кодированные значения факторов и в -м опыте.

Для расчета коэффициентов уравнения регрессии составляется план в соответствии с табл. 4.2–табл. 4.6, строки которой и заполняются в процессе вычислений.

Каждая строка табл.4.6 заполнена, как это следует из таблицы, одними и теми же числами. Однако знаки при этих числах разные, они меняются в соответствии с правилом чередования знаков расчетной матрицы. Числа в столбцах суммируются (с учетом знаков). Полученные значения заносятся в строку суммы.

Следовательно, модель имеет следующий вид:

Таблица 4.6

Расчет коэффициентов уравнения регрессии

№
1	2	3	4	5	6	7	8	9
1	–81,08	–81,08	–81,08	+81,08	+81,08	+81,08	–81,08	81,08
2	+85,65	–85,65	–85,65	–85,65	–85,65	+85,65	+85,65	85,65
3	–82,27	+82,27	–82,27	–82,27	+82,27	–82,27	+82,27	82,27
4	+90,40	+90,40	–90,40	+90,40	–90,40	–90,40	–90,40	90,40
5	–84,95	–84,95	+84,95	+84,95	–84,95	–84,95	+84,95	84,95
6	+89,95	–89,95	+89,95	–89,95	+89,95	–89,95	–89,95	89,95
Окончание табл. 4.6
1	2	3	4	5	6	7	8	9
7	–85,25	+85,25	+85,25	–85,25	–85,25	+85,25	–85,25	85,25
8	+88,25	+88,25	+88,25	+88,25	+88,25	+88,25	+88,25	88,25
∑	20,7	4,56	9,04	1,6	4,72	7,36	5,6	687,84
	b1= 2,59	b2= 0,57	b3=1,13	b12= 0,20	=–0,59	=–0,92	=–0,70	85,98

Вычислив коэффициенты регрессии, проверяют их значимость. Одним из способов является оценка с помощью -критерия Стьюдента. Расчётное значение критерия Стьюдента вычисляют по выражению:

, (4.12)

где – ошибка в определении -го коэффициента;

, (4.13)

где – дисперсия -го коэффициента регрессии (она одинакова для всех коэффициентов модели).

(4.14)

Полученный -критерий сравнивают с табличным (прил. 2). Коэффициент регрессии значим, если .

Критерий Стьюдента вычисляют для каждого коэффициента регрессии. Статистически незначимые коэффициенты исключаются из уравнения регрессии.

Для расчета критерия Стьюдента найдём дисперсию оценок коэффициентов

и их квадратичную ошибку:

.

Вычислим расчётные значения -критерия Стьюдента и сравним с :

; ; ; ; ; ; .

Табличное значение критерия Стьюдента при доверительной вероятности 0.95 и числе степеней свободы составляет (прил. 2).

Очевидно, что все оценки, за исключением , оказались значимыми. Тогда модель объекта будет иметь вид:

Проверка уравнения на адекватность производится с использо-ванием – критерия Фишера:

. (4.15)

где – дисперсия адекватности и дисперсия воспроизводимости.

Дисперсия адекватности (остаточная дисперсия) , которая характеризует рассеяние эмпирических значений относительно расчётных , определяемых по уравнению регрессии находится следующим образом:

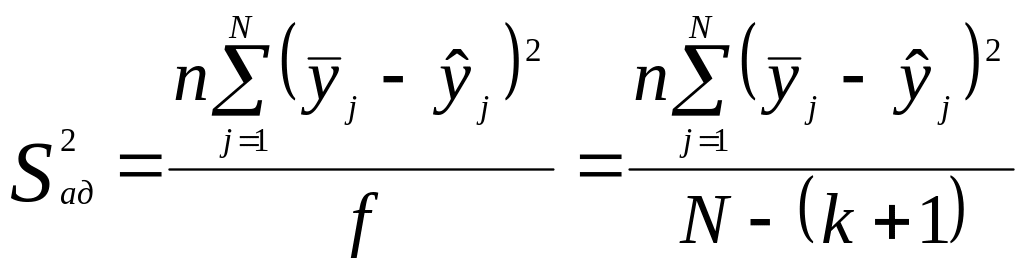, (4.16)

где п – число повторных опытов; – среднее арифметическое значение параметра оптимизации в -м опыте; – значение параметра оптимизации, вычисленное по модели для условий -го опыта; – число степеней свободы равное – число факторов.

Для проведения необходимых вычислений вновь используется расчетная матрица при условии, что столбец исключается из анализа.

Столбцы и т. д. в расчетной матрице заполняются произведениями кодированных значений факторов и их взаимодействий на соответствующие значения коэффициентов при них. Тогда абсолютные значения чисел в каждом из столбцов будут отличаться лишь знаками. Причем для положительных коэффициентов знаки чисел в столбцах будут чередоваться по указанному выше правилу. Для отрицательных коэффициентов все знаки поменяются на противоположные, так как знак минус в матрице, умноженный на знак минус при коэффициенте, даст плюс, а плюс, умноженный на минус, даст минус (табл. 4.7).

Просуммировав построчно значения чисел в табл. 4.7, получаем расчетные значения выходной величины . Далее построчно определяем разности , значения которых возводятся в квадрат.

Далее находим дисперсию адекватности

и получаем расчётное значение критерия Фишера

.

Табличное значение критерия определяется по числам степеней свободы и (прил. 6). Если , то уравнение регрессии адекватно исследуемому технологическому процессу. Следовательно, это уравнение может служить основой для отыскания оптимальных режимов осуществления процесса.

В рассматриваемом примере табличное значение критерия Фишера при , и доверительной вероятности составляет (прил. 6). Так как расчетное значение критерия Фишера существенно меньше табличного, следовательно, модель является адекватной.