Пример статистической обработки результатов эксперимента с малым числом испытаний
При испытании пряжи на разрыв получены следующие значения её прочности (Н): 199, 239, 224, 229, 224, 234, 219, 300, 214, 218.
Расположим данные в порядке возрастания: 199, 214, 218, 219, 224, 224, 229, 234, 239,300.
Известно, что распределение значений прочности пряжи подчиняется нормальному закону распределения. Пользуясь формулами (2.3) – (2.5), находим:
;
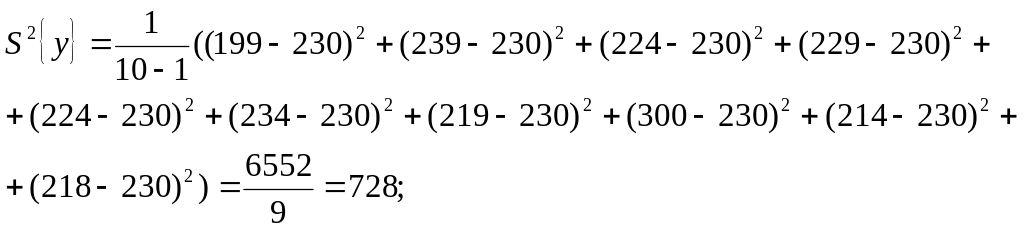
Значение критерия Смирнова-Грабса для максимального значения рассчитываем по формуле (2.6):
.
По
прил. 1
находим, что
,
т. к. при заданной доверительной
вероятности
,
то значение
нужно считать резко выделяющимся и его
целесообразно исключить из дальнейшей
обработки.
3.Теперь
проверим, относится ли
к резко выделяющимся значениям. Снова
определяем те же характеристики.
После
исключения
остается
измерений и поэтому
Определяем расчетное значение критерия (2.7):
Находим
,
т.к.
,
следовательно,
не является резко выделяющимся значением.
4. Далее рассчитываем коэффициент вариации и квадратическую неровноту (2.8), (2.9):
%.
5.
Определяем абсолютную и относительную
ошибки (2.10), (2.11) при
(прил. 2):
%.
6. Доверительный интервал из (2.12) равен:
7.
Находим доверительный объем выборки
при
и
по формуле (2.13):
;
т.к.
,
то искомое число
будет равно 15 (прил.
3).
Если
нужно найти
при величине ошибки
%
и
,
то
.
Так как
0,37,
и задана относительная ошибка
,
то
определяем по формуле (2.14).
.
3.3. Практическая работа № 3
Тема работы: статистический анализ результатов эксперимента при исследовании технологического процесса.
Цель работы: Изучение методов расчета числовых характеристик совокупности случайных величин, их достоверности и доверительного объема выборки.
Методика и порядок выполнения:
1. Ознакомиться с причинами возникновения ошибок измерений, классификацией погрешностей, методикой обработки выборки с малым числом измерений, правилами приближенных вычислений. Основные понятия и определения занести в таблицу 3.1.
Таблица 3.1
Основные понятия и определения
Термин |
Определение |
|
|
2. Провести статистическое исследование совокупности случайных величин, характеризующих изменение параметров технологических процессов или свойств продуктов.
Определить
в соответствии с заданием (табл. 3.2)
числовые характеристики совокупности
из десяти случайных величин, их
доверительный интервал и объем выборки,
обеспечивающий заданную точность
(относительную ошибку
)
и надежность (доверительную вероятность
).
Таблица 3.2
Задания к практической работе 3
Номер варианта |
Результаты эксперимента |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
1 |
4,71 |
4,75 |
5,15 |
5,24 |
5,55 |
4,49 |
4,26 |
5,09 |
2,26 |
5,03 |
2 |
4,76 |
4,79 |
5,22 |
5,27 |
5,60 |
4,58 |
4,35 |
5,18 |
7,72 |
5,07 |
3 |
6,52 |
7,52 |
6,86 |
7,19 |
7,57 |
6,90 |
7,40 |
7,52 |
7,66 |
4,52 |
4 |
5,67 |
6,11 |
6,01 |
6,21 |
6,55 |
5,54 |
5,6 |
6,13 |
9,13 |
6,19 |
5 |
0,97 |
1,37 |
0,86 |
0,97 |
1,05 |
0,48 |
1,04 |
1,03 |
1,15 |
1,01 |
6 |
4,96 |
4,91 |
4,77 |
4,81 |
4,01 |
3,02 |
4,37 |
4,25 |
4,20 |
4,32 |
7 |
50,0 |
49,6 |
48,6 |
47,9 |
48,1 |
66,2 |
50,3 |
51,1 |
52,7 |
51,0 |
8 |
59,0 |
58,8 |
57,3 |
59,1 |
55,5 |
54,3 |
52,8 |
59,4 |
32,1 |
57,5 |
9 |
69,8 |
70,0 |
68,2 |
68,7 |
78,0 |
66,2 |
50,0 |
65,1 |
70,8 |
70,3 |
10 |
9,5 |
9,7 |
9,9 |
11,0 |
9,1 |
10,0 |
9,2 |
4,6 |
10,2 |
8,8 |
11 |
41,1 |
40,9 |
41,8 |
41,5 |
40,9 |
39,4 |
41,0 |
30,2 |
40,3 |
40,6 |
12 |
41,6 |
41,3 |
42,2 |
42,1 |
41,3 |
44,0 |
59,4 |
42,4 |
47,0 |
43,4 |
13 |
75,6 |
82,4 |
75,3 |
69,9 |
76,3 |
56,2 |
74,3 |
69,9 |
71,0 |
75,0 |
14 |
58,2 |
81,4 |
58,3 |
55,4 |
57,6 |
56,1 |
54,5 |
54,9 |
56,9 |
54,2 |
15 |
1,07 |
1,71 |
2,03 |
1,65 |
1,38 |
1,66 |
1,69 |
1,39 |
1,48 |
1,67 |
16 |
2,97 |
2,86 |
2,47 |
3,21 |
3,17 |
2,61 |
2,62 |
2,72 |
4,59 |
2,67 |
17 |
3,01 |
2,91 |
2,50 |
3,16 |
3,11 |
3,39 |
3,08 |
3,13 |
3,31 |
3,10 |
18 |
4,84 |
4,87 |
4,47 |
5,14 |
5,23 |
4,58 |
3,35 |
5,18 |
5,24 |
5,07 |
19 |
3,83 |
3,76 |
3,37 |
4,07 |
4,09 |
3,92 |
4,06 |
5,29 |
4,01 |
4,02 |
Окончание табл. 3.2 |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
20 |
0,85 |
0,90 |
0,92 |
0,86 |
0,93 |
0,81 |
0,80 |
0,79 |
0,47 |
0,83 |
21 |
2,30 |
2,16 |
2,32 |
3,35 |
2,37 |
2,35 |
2,22 |
2,13 |
2,20 |
2,29 |
22 |
23,5 |
21,9 |
23,2 |
29,7 |
24,1 |
10,9 |
22,8 |
23,4 |
21,7 |
23,0 |
23 |
30,4 |
39,7 |
42,1 |
44,1 |
42,7 |
44,0 |
43,1 |
42,3 |
43,7 |
48,8 |
24 |
0,79 |
0,81 |
0,85 |
0,95 |
0,84 |
0,18 |
0,75 |
0,82 |
0,86 |
0,80 |
25 |
1,88 |
1,89 |
1,79 |
1,76 |
1,86 |
0,88 |
1,77 |
1,85 |
1,90 |
2,00 |
Рассчитать оценки:
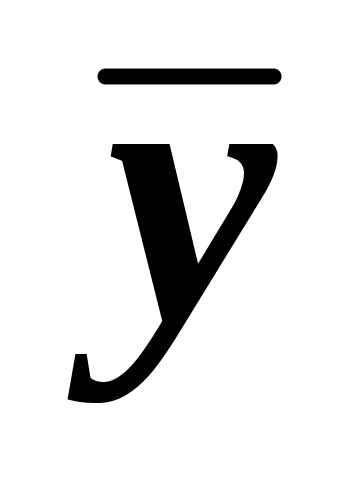– математического ожидания (среднее),
– дисперсии и
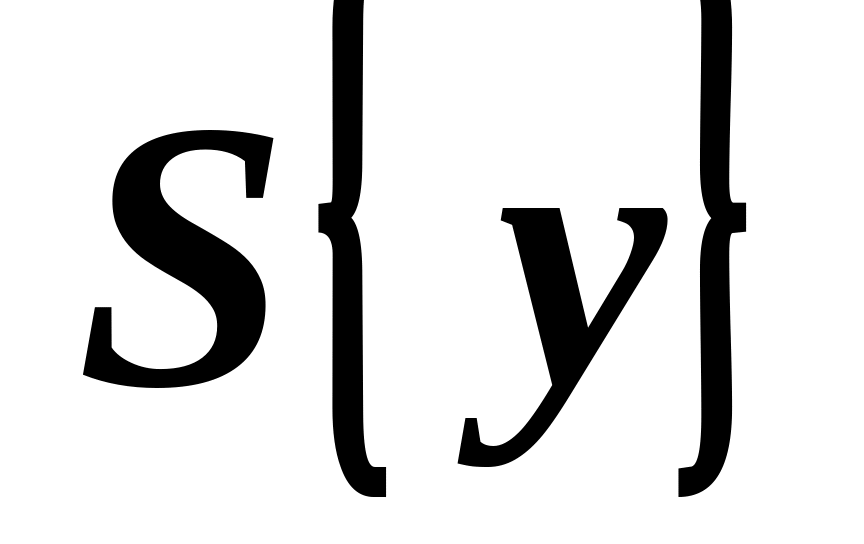– среднего квадратичного отклонения
для выборки случайных величин, используя
соответственно формулы (3.1), (3.2), (3.3).Исключить резко выделяющиеся случайные величины полученной совокупности, используя критерий Смирнова-Грабса по формулам (3.4), (3.5).
Для вновь полученного количества опытов рассчитать оценки математического ожидания, дисперсии и среднего квадратического отклонения, а также коэффициент вариации и квадратическую неровноту
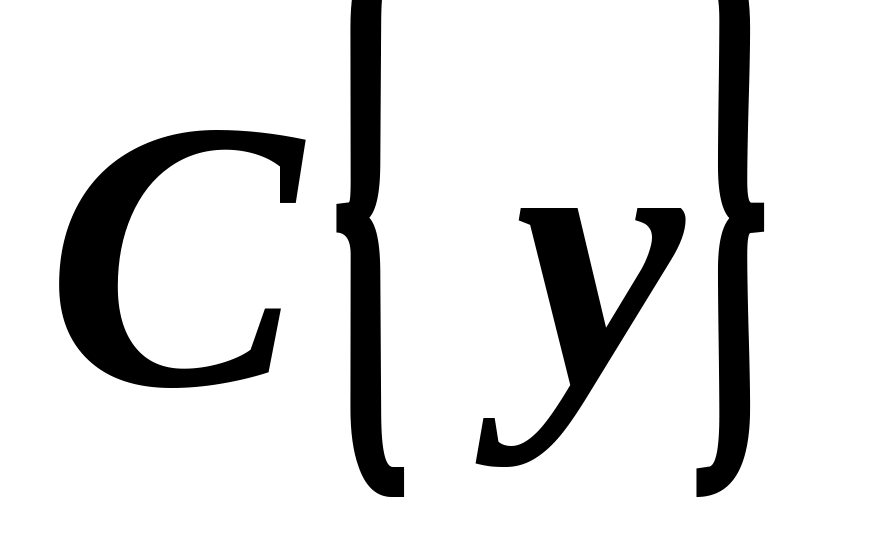по формулам (3.6), (3.7).Определить абсолютную и относительную ошибки среднего и границы доверительного интервала при доверительной вероятности
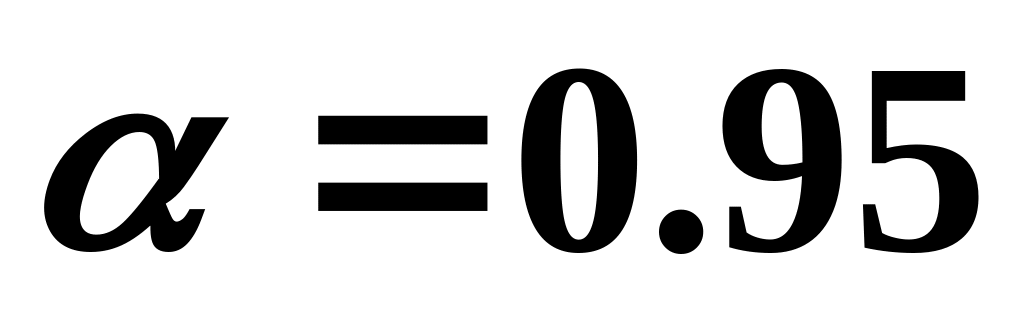по формулам (3.8) – (3.10).Рассчитать доверительный объем выборки при заданных величинах ошибки
и доверительной вероятности
по формулам (3.11), (3.12).
Расчет числовых характеристик для совокупности случайных величин проводится в помощью электронных микрокалькуляторов или на ЭВМ по специальным программам.
3. Провести анализ результатов статистической обработки результатов эксперимента и сформулировать выводы.