5.4. Моделі систем управління запасами з двома рівнями запасів

У цих моделях використовується -стратегія управління. При використанні цієї стратегії у моменти перевірок замовляється партія, яка поповнює рівень запасів (для системи з обліком замовлень) або сумарний обсяг наявних запасів і ще невиконаних замовлень на поповнення (для системи із втратою замовлень) до рівня Для прийнятих тут функцій витрат при випадковому попиті -стратегія зазвичай оптимальна, якщо реєструються усі замовлення, які надходять за час дефіциту запасів. Оптимальну -стратегію наближено можна замінити -стратегією або -стратегією. Нижче ми розглянемо вираз для середніх річних витрат у системі з обліком замовлень, коли використовується -стратегія, попит розподілений за законом Пуассона і час поставки постійний. Обчислимо середні річні витрати, підрахувавши середні витрати за один цикл роботи системи і помноживши цей результат на загальну кількість циклів.

Щоб одержати у явній формі вираз для середніх річних витрат приймемо такі припущення:

 попит є стаціонарним випадковим процесом;

 попит у різні періоди часу є незалежним;

 час поставки постійний.

Раніш ніж зосередити увагу на випадку пуассонівського розподілу попиту, обчислимо для довільного розподілу попиту стаціонарні ймовірності того , що до моменту закінчення перевірки рівень запасів у системі дорівнює Якщо нам буде відомий розподіл імовірностей то ми зможемо обчислити середні річні витрати точно також, як це було зроблено для -моделі.

Випадковий процес переходів із стану у стан може розглядатись як марковський ланцюг із скінченим числом станів. Виведемо рівняння, яким повинні задовольняти ймовірності

Рівень запасів у системі зразу ж по закінченню перевірки може прийняти одне із значень Для того, щоб обчислити перехідні ймовірності припустимо, що до закінчення чергової перевірки рівень запасів у системі дорівнює Необхідно обчислити ймовірність того, що до кінця наступної перевірки рівень запасів у системі складе Якщо то ця ймовірність дорівнює нулю, оскільки такі переходи неможливі. Якщо то . Коли і імовірність переходу буде дорівнювати , де функція розподілу, пов’язана із Коли і тобто у випадку, якщо замовлення на склад не надходили, то цьому випадку відповідає ймовірність

Таким чином

.

Стаціонарні ймовірності задовольняють наступній системі рівнянь

(5.43)

Є очевидним, що даний розподіл не є рівномірним, як це було раніше, оскільки стану повинна відповідати більша, ніж іншим станам, імовірність.

Знайдемо ймовірності станів у явному вигляді. Обчисливши середні витрати на інтервалі або у циклі між моментами послідовної подачі двох замовлень на поповнення і помноживши одержаний результат на середню кількість таких інтервалів у рік, спочатку буде виведений точний вираз для сумарних середніх річних витрат. Із цього виразу будуть одержані ймовірності .

Обмежуючись випадком, коли попит породжується пуассонівським потоком вимог одиничної величини, одержимо явний вираз для сумарних середніх річних витрат як функцій від Із цього виразу ми одержимо загальний розв’язок рівнянь (5.43).

Нехай є ймовірність того, що попит за період складе одиниць. Тоді у наслідок припущення про незалежність попиту у різні періоди роботи системи ймовірність того, що попит за періодів складе одиниць запасу, дорівнює де – n-кратна композиція Нехай означає момент перевірки, і нехай зразу ж після прийняття рішення про необхідність поповнення складських запасів фіктивний рівень запасів у системі дорівнює – сума середніх витрат по зберіганню і обліку замовлень на інтервалі від до де час поставки.

Припустимо, що замовлення на поповнення подається в момент Починаючи з цього моменту до включно, не подається більше жодного замовлення, а фіктивний рівень запасів до моменту дорівнює Це означає, що, починаючи із за час на склад замовлено в точності одиниць запасу. Імовірність цієї події дорівнює Середні витрати зберігання і середня вартість обліку замовлень на інтервалі від до складе Далі, починаючи з наступний замовлення може бути поданий через один період, два періоди і т.д. Якщо за періодів не виникла необхідність у замовленні, то на -му періоді витрати зберігання і витрати на враховані замовлення складуть при умові, що до початку -го періоду фіктивний рівень запасів у системі склав одиниць. Імовірність того, що цикл складається більше ніж із періодів, а рівень запасів до початку -го періоду складе дорівнює Таким чином, в середньому витрати зберігання і витрати на облік замовлень у -му періоді роботи системи складуть

У циклі завжди є щонайменше один період, а на першому періоді сумарні витрати складають грош. одиниць, оскільки зразу ж після подачі замовлення фіктивний рівень запасів у системі дорівнює Середні витрати на зберігання запасів і враховані замовлення за один цикл знаходяться підсумовуванням наведених вище виразів по всіх Таким чином, ці середні витрати дорівнюють

якщо, за означенням, покласти

Визначивши середні витрати на зберігання запасів і облік замовлень за цикл, ми повинні тепер знайти середнє число циклів у рік, тобто величину, обернену до середньої тривалості циклу. Тривалість періоду дорівнює помноженому на середнє число періодів у циклі.

Обчислимо середнє число періодів у циклі. Цикл в точності дорівнює одному періоду, якщо попит у першому періоді циклу перевищує величину Імовірність цієї події дорівнює де дорівнює одиниці мінус функція розподілу, яка одержується підсумовуванням імовірностей від 0 до тобто

або .

Розглянемо тепер імовірність того, що цикл складається в точності із періодів Якщо у перших періодах після подачі чергового замовлення із складу було замовлено одиниць запасу і попит у -му періоді перевищить або виявиться що найменше рівним то цикл буде триватись в точності періодів. Звідси ймовірність того, що цикл складається в точності із періодів, дорівнює

Отже, середнє число періодів у циклі складає

Якщо скористатись введеним вище означенням то це можна записати у вигляді

Тепер можна записати вираз для сумарних річних витрат. Якщо, як і звичайно, вартість подачі замовлення і вартість перевірки, то сумарні річні витрати дорівнюють

(5.44)

Якщо відомий розподіл попиту, то можна у явній формі виписати вирази для Раніш ніж зробити це для випадку, коли попит породжується пуассонівським потоком вимог одиничної величини, знайдемо із (5.44) стаціонарні ймовірності , знаходячи тим самим розв’язок системи (5.43).

Зауважимо, що величина

представляє собою відповідні витрати зберігання запасів і обліку замовлень за період. Але, за означенням середні витрати за період дорівнюють

Звідси випливає, що

(5.45)

Можна довести, що це дійсно так [8], і які визначаються за формулою (5.45), задовольняють системі рівнянь (5.43).

Звернемось тепер до випадку, коли обсяг попиту розподілений за законом Пуассона. Тоді

Тепер можна виписати явний вираз для Це вже було зроблено для -моделі. Якщо фіктивний рівень запасів в момент дорівнював то середня кількість замовлень, врахованих на інтервалі від до дорівнює

(5.46)

Аналогічно середня інтегральна нестача за період від до складає

(5.47)

Нарешті, середня кількість одиниць запасу на інтервалі від до дорівнює

(5.48)

Підсумовуючи одержані складові витрат, одержимо середні витрати на зберігання і облік замовлень на інтервалі від до

(5.49)

З урахуванням (5.49) середні загальні річні витрати, які були визначені у (5.44), тепер будуть визначатись таким виразом:

(5.50)

Оптимізація даної моделі за критерієм, визначеним виразом (5.55), класичними методами є складною задачею, оскільки функція залежить від параметрів досить складним чином. Тому, як і у попередніх моделях, для чисельної реалізації даної моделі застосуємо алгоритм дискретної оптимізації. Розглянемо алгоритм, у якому попит розподілений за законом Пуассона.

Алгоритм реалізації моделі

 задаємо вхідні дані моделі

 записуємо вираз для розподілу Пуассона і його додаткову функцію розподілу

 визначаємо складові функції витрат:

 визначаємо функцію середніх річних витрат ;

 задаємо діапазони можливих значень параметрів відповідно і послідовність значень параметра ;

 для кожного представляємо значення функції у вигляді масиву (матриці) , елементи якого дорівнюють де

 мінімальне значення функції знаходимо як мінімальний елемент матриці за допомогою функції Mathcad ;

 визначаємо індекси мінімального елемента масиву і знаходимо оптимальні значення

Приклад 5.5. Розглянемо систему військового постачання, у якій зберігається деякий дорогокоштуючий матеріал. Попит на нього можна вважати розподіленим за законом Пуассона із середньою інтенсивністю 100 одиниць у рік. Вартість подачі замовлення на поповнення запасу складає 4 тис. грн., вартість перевірки рівня запасів – 2 тис. грн. Ціна одиниці дорівнює 10 тис. грн. незалежно від розміру замовлення. Усі замовлення, які надходять у систему, коли в ній нема запасів, реєструються, і втрати від кожного такого врахованого замовлення оцінюється у 20 тис. грн. незалежно від часу, який пройшов з моменту реєстрації замовлення. Втрати, пов’язані із часом дефіциту матеріалу, обходяться у 2 тис. грн. Час поставки є випадковою величиною із середнім 0,1 року. Коефіцієнт витрат утримання запасів дорівнює 0,2. Застосовуючи -стратегію управління запасами, визначимо оптимальні значення фіктивного запасу рівня подачі замовлення і період перевірки рівня запасів

_{Алгоритм у Mathcad}

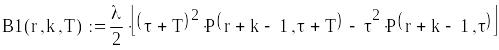
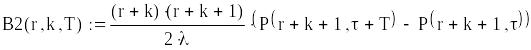
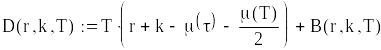
Перетворення масиву значень функції у матрицю при і визначення оптимальних значень

_{Фрагмент матриці Z}

_{Мінімальне значення середніх річних витрат}

Коментар. Оптимальна стратегія управління запасами у даній системі має такі параметри: оптимальний фіктивний рівень запасів (обсяг наявних запасів плюс обсяг ще невиконаних замовлень) оптимальний рівень подачі замовлення оптимальний період перевірки стану запасів (1,6 місяця). Мінімальні витрати на функціонування системи управління запасами при даній стратегії складатимуть 85,4 тис. грн. ▲