5.3. Точні моделі управління запасами з постійним рівнем запасів

Розглянемо спочатку точні рівняння для -моделі при постійному часі поставок і попиті, розподіленому за законом Пуассона. Ці рівняння можна одержати із рівнянь підрозділу 5.2.1, якщо покласти в них Насамперед із (5.13) видно, що імовірність подачі замовлення у довільний момент часу дорівнює

(5.33)

де

Обчислимо середнє число замовлень врахованих за рік, і середню інтегральну нестачу за рік . Їх легко одержати, поклавши Отже будемо мати

.

Таким чином, середнє число замовлень, врахованих за рік, і середня інтегральна нестача за рік дорівнюють

(5.34)

.

(5.35)

Враховуючи одержані вирази, середні річні витрати дорівнюватимуть

(5.36)

.

Звідси

(5.37)

=

Найменше , яке мінімізує функцію є найбільше для якого Для знаходження , яке задовольняє вказаній умові, можна застосувати чисельні методи. Втім, у багатьох випадках можна знехтувати доданками, які залежать від у порівнянні із членами, які залежать від У результаті цього вираз для спрощується і має вигляд

(5.38)

Відмітимо, що (5.37) справедливе для всіх тоді як (5.38) виконується тільки для досить великих Т.

Оптимальні значення простіше всього визначати, застосовуючи алгоритм перетворення масиву значень у відповідну матрицю і визначаючи її мінімальний елемент та його індекси, за якими остаточно знаходяться . Аналогічний алгоритм можна побудувати, перетворюючи масив значень функції у матрицю і знаходячи індекси першого її елемента, який є додатним.

Виведемо тепер точні рівняння для -моделі у випадку, коли неперервна величина, а обсяг попиту за довільний проміжок часу розподілений за нормальним законом із середнім і дисперсією Для того, щоб скористатись результатами попереднього розділу, треба у виведених там рівняннях покласти і перейти до границі при (у дискретному випадку ми покладали Очевидно, що у неперервному випадку повинна дорівнювати 1, оскільки ймовірність того, що сумарний попит за довільний проміжок часу відмінний від нуля, дорівнює 1. До такого ж висновку приводить співвідношення (5.25), якщо покласти у ньому і припустити, що у області від’ємних значень аргументу щільність імовірності досить близька до нуля.

Безпосередньо із (5.25) випливає, що

Аналогічно із (5.28) і (5.29) маємо

(5.40)

Таким чином, сумарні середні річні витрати дорівнюють

(5.41)

де При фіксованому Т оптимальне значення визначається із наступного рівняння:

(5.42)

де

,

Алгоритм реалізації моделі

 задаємо вхідні дані моделі

 записуємо функцію щільності ймовірності нормованого нормального розподілу і його додаткову функцію розподілу ;

 визначаємо середню кількість врахованих за рік замовлень

 визначаємо середню інтегральну нестачу товарів за рік

 визначаємо функцію середніх річних витрат .

Для знаходження оптимальних значень застосуємо алгоритми дискретної оптимізації (перебірний алгоритм):

 задаємо діапазони можливих значень параметрів відповідно і

 представляємо масив значень функції у вигляді матриці , елементи якої де крок зміни параметра Т,

Мінімальне значення функції знаходимо як мінімальний елемент матриці за допомогою функції Mathcad . Далі визначаємо індекси мінімального елемента матриці і знаходимо оптимальні значення

 визначаємо гарантійний запас

Приклад 5.4. Розглянемо алгоритм реалізації -моделі системи управління запасами з параметрами, аналогічними прикладу 5.2. Попит розподілений за нормальним законом із середньою інтенсивністю 100 одиниць у рік і середнім квадратичним відхиленням .

Визначимо оптимальну політику управління запасами у даній системі, використовуючи -стратегію.

Алгоритм реалізації даної моделі аналогічний алгоритму попередньої моделі. Відповідні параметри нормального розподілу попиту дорівнюють

_{Алгоритм у Mathcad}

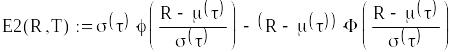
Перетворення масиву значень функції у матрицю і визначення оптимальних значень

Фрагмент матриці

_{Мінімальне значення середніх річних витрат}

Індекси мінімального елемента матриці і оптимальні значення параметрів

Функціональні характеристики:

 Середня кількість врахованих замовлень за рік

 Середня інтегральна нестача товарів за рік

 Середній обсяг запасу у системі за рік

 Середній гарантійний запас

Коментар. Оптимальна стратегія управління запасами за даною моделлю характеризується такими параметрами: фіктивний рівень запасів в момент перевірки одиниць, період перевірки року (2,4 місяця). Середні мінімальні витрати на функціонування системи складуть грош. од.

Ці результати показують, що розглянута у даному прикладі -стратегія управління запасами дає більші витрати ніж -стратегія, розглянута у попередньому прикладі. Це підтверджує той факт, що коли вартість перевірки системи менша вартості подачі замовлення ( , перевагу має -стратегія. ▲