5.2.2. Попит розподілений за нормальним законом

Розглянемо алгоритм реалізації - моделі, коли попит за час є неперервна випадкова величина розподілена за нормальним законом із середнім і дисперсією Будемо також припускати, що величини також неперервні.

Нехай є щільність розподілу величини попиту за період Припускаючи, що попит у різних періодах незалежний, покажемо, що зразу ж після перевірки рівень запасів у системі розподілений рівномірно.

Нехай означає стаціонарну ймовірність події, яка полягає у тому, що фіктивний рівень запасів після закінчення перевірки вміщений у межах Можна показати, що щільність повинна задовольняти наступному рівнянню:

(5.23)

де

Тут , якщо якщо Зауважимо, що

Звідси видно, що при є розв’язком рівняння (5.23). А оскільки

то

(5.24)

Обчислимо тепер окремі складові загальних середніх річних витрат для випадку, коли попит розподілений за нормальним законом.

На перевірки протягом року витрачається сума у грош. одиниць, закази обходяться у середньому у грош. одиниць у рік. Тут є ймовірність того, що при довільній перевірці подається заказ. Ця ймовірність дорівнює

Звідси, приймаючи до уваги, що при наближенні розподілу ймовірностей за допомогою нормального розподілу значення щільності ймовірності і функції розподілу при досить близькі до нуля, одержимо

(5.25)

Легко бачити, що середні річні витрати зберігання дорівнюють

(5.26)

де як і раніше, середня інтегральна нестача за рік, тобто середня кількість врахованих невиконаних замовлень.

Визначимо тепер вирази для середньої кількості замовлень, які враховуються за рік, і для середньої інтегральної нестачі за рік. Для цього використовуються ті ж прийоми, що і у дискретному випадку, розглянутому у попередньому пункті. Середня кількість врахованих за рік замовлень складає

(5.27)

Далі маємо

.

Звідси одержуємо вираз для середньої кількості замовлень, врахованих за рік

, (5.28)

де

.

Аналогічно одержуємо вираз для інтегральної середньої нестачі запасу

(5.29)

.

Визначення проводиться у декілька етапів. Спочатку одержуємо

(5.30)

Далі

Звідкіля

(5.31)

Загальні середні річні витрати тепер можуть бути записані у наступному вигляді:

(5.32)

де

а визначаються за формулами (5.28) і (5.29) відповідно.

На жаль, функція у загальному випадку не є опуклою функцією Це ускладнює задачу обчислення оптимальних значень оскільки у функції може виявитись декілька локальних мінімумів, тим більше, що знайти хоча б який розв’язок рівнянь досить складно. Таким чином, як і у дискретному випадку для знаходження оптимальних представляється необхідним використання алгоритму дискретної оптимізації.

Приклад 5.3. Розглянемо -модель системи управління запасами, у якій попит розподілений за нормальним законом із середньою інтенсивністю 100 одиниць у рік і середнім квадратичним відхиленням . Усі інші параметри моделі такі ж самі, як і у прикладі 5.2.

Визначимо оптимальну політику управління запасами у даній системі, використовуючи -стратегію.

Загальний алгоритм реалізації даної моделі аналогічний алгоритму попередньої моделі. Відповідні параметри нормального розподілу попиту дорівнюють Наведемо алгоритм реалізації моделі у Mathcad.

_{Алгоритм у Mathcad}

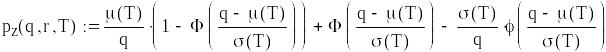
Перетворення масиву значень функції при у матрицю і визначення оптимальних значень

_{Мінімальне значення середніх річних витрат}

Індекси мінімального елемента матриці і оптимальні значення параметрів при

Перетворення масиву значень функції при знайденому у матрицю і визначення оптимальних значень

Індекси мінімального елемента матриці і оптимальні значення параметрів при

Функціональні характеристики:

 Середня кількість врахованих замовлень за рік ;

 Середня інтегральна нестача товарів за рік

 Середній обсяг запасу у системі за рік

 Середній гарантійний запас .

Коментар. Оптимальна стратегія управління запасами за даною моделлю характеризується такими параметрами: обсяг поставки одиниць товару, фіктивний рівень запасів в момент перевірки одиниць, період перевірки року (3,24 місяця), гарантійний запас одиниць товару. Мінімальні витрати на функціонування системи складуть грош. од.

Ці результати показують, що розглянута системи управління запасами із попитом, розподіленим за нормальним законом, у порівнянні із системою, у якій попит розподілений за законом Пуассона, більш економічна за сумарними річними витратами – грош. од. Це є наслідком того, що у першій системі середній річний запас менше середнього річного запасу у другій системі – од. товару. Також і менший гарантійний запас од. товару. Окрім цього, період перевірок рівня запасів у першій системі більше аналогічного періоду у другій системі – року, тобто перевірки у першій системі проводяться рідше ніж у другій. ▲