4.7. Моделі систем управління запасами при випадковому часі поставок

Для простих наближених моделей управління запасами припускалось, що час поставки випадковий і має щільність розподілу ймовірності Для точних моделей, розглянутих вище, час поставки вважався постійним. Якщо кількість невиконаних замовлень не стає більшим одиниці, то при побудові точних моделей ніяких теоретичних труднощів не виникає. Треба лише провести усереднення очікуваних річних витрат в момент по всіх можливих значеннях Так, якщо середні річні витрати для заданого то середні річні витрати, усереднені по складуть

(4.53)

Потім функцію треба мінімізувати. Легко бачити, що безпосередньо обчислюється за допомогою безумовного розподілу попиту за час поставки.

Розглянемо тепер ситуацію, коли допускається наявність одного невиконаного замовлення у будь-який момент часу. Зазвичай на практиці у будь-який момент часу можуть бути два або більше невиконаних замовлень, але інтервали між ними настільки великі, що між ними відсутня будь-яка взаємодія. Тому із достатньо задовільним наближенням можна вважати, що часи поставок не залежні і не перетинаються. При цій умові для ймовірності того, що наявний запас в момент дорівнює , справедливе співвідношення

(4.54)

де безумовний розподіл попиту за час поставки.

Припускаючи часи поставок незалежними і одночасно не допускаючи можливості їх перетину, зручно прийняти у якості гама-розподіл. Якщо попит розподілений за законом Пуассона, а час поставки має гама-розподіл, то безумовний розподіл попиту за час поставки буде від’ємним біноміальним. Тому при обчисленні середніх витрат у виразах для треба розподіл Пуассона замінити на бета-розподіл У тих випадках, коли неперервні величини, а попит має нормальний розподіл, одночасно припускають, що безумовний розподіл попиту також є нормальним. Тоді формули параграфу 4.4 можна використовувати без змін.

Y(t) Y Рис. 4.10. Графік рівня запасу

Розглянемо наближену модель системи управління запасами при випадковому часі поставок, у якій рівень запасу контролюється неперервно, а замовлення розміром q подається тоді, коли цей рівень досягає деякої точки поновлення запасу . Рівень , при якому знову подається замовлення, є функцією періоду часу між подачею замовлення і його виконанням. У даній моделі допускається незадовільнений попит, як показано на рис. 4.10. Задача полягає у знаходженні оптимальних значень і , які мінімізують сумарні очікувані витрати системи управління запасами, віднесені до одиниці часу (за одиницю часу приймемо рік). Ці витрати включають як витрати на поповнення замовлення і його зберігання, так і втрати, пов’язані із незадовільненим попитом.

У моделі прийняті наступні припущення:

1. Строк виконання замовлення, тобто відрізок часу з моменту його подачі до моменту поставки, стохастичний.

2. Незадовільнений протягом терміну виконання замовлення попит накопичується.

3. Розподіл попиту протягом часу виконання замовлення не залежить від моменту виникнення попиту.

4. У будь-який момент часу є не більше одного невиконаного замовлення.

Введемо позначення:

– щільність умовної ймовірності попиту х упродовж строку виконання замовлення (t > 0);

– щільність імовірності часу виконання замовлення;

f(х) – щільність безумовної ймовірності попиту х упродовж строку виконання замовлення :

Q – очікуваний сумарний річний попит;

– точка подачі замовлення;

q – обсяг замовленої у циклі продукції;

– витрати на оформлення одного замовлення;

– питомі витрати на зберігання запасу;

– питомі втрати від дефіциту.

Сумарні річні витрати містять:

 очікувані витрати на зберігання продукції;

 середні витрати на оформлення замовлення;

 очікувані втрати від дефіциту.

Середні витрати на поповнення запасу дорівнюють , де – середня кількість замовлень у рік.

Очікувані витрати на зберігання обчислюються на основі очікуваних наявних рівнів запасу на початок і кінець циклу. На початку циклу (в момент поставки замовлення розміром q) очікуваний рівень запасу дорівнює , а у кінці циклу він дорівнює де М – символ математичного сподівання. Таким чином, середній рівень запасу за цикл (отже і за рік) визначається виразом

(4.55)

При вказаній вище функції f(x)

(4.56)

Наведена формула для одержана в результаті усереднення очікуваних запасів на початку і кінці часового циклу, тобто величини і відповідно. При цьому ігнорується випадок, коли величина (розмір дефіциту) може бути від’ємною, що є одним із спрощуючих припущень моделі.

Нехай R – розмір дефіциту за цикл. Тоді

Дефіцит виникає при . Отже, очікуваний розмір дефіциту за цикл дорівнює:

(4.57)

Оскільки в моделі припускається, що пропорційне лише обсягу дефіциту, то очікувані втрати, пов’язані із незадоволеним попитом, за один цикл дорівнюють Оскільки упродовж року розміщуються приблизно замовлень, то очікувані втрати, обумовлені дефіцитом, складають за рік.

Таким чином сумарні річні витрати у системі управління запасами дорівнюють

(4.58)

Відмітимо, що втрати від дефіциту припускаються пропорційними розміру дефіциту тільки тоді, коли не враховується тривалість дефіциту. Це також є спрощуючим припущенням в моделі, оскільки у випадку заборгованості товару втрати від дефіциту залежать від його тривалості.

Позначимо через і – оптимальні значення обсягу поставок і рівня запасу. Вони визначаються із наступних рівнянь

Із першого рівняння маємо

(4.59)

а із другого

(4.60)

Оптимальні значення для одержується розв’язанням системи рівнянь (4.59), (4.60). Ця система є нелінійною. У Mathcad нелінійні системи розв’язується за допомогою функцій Minerr( ) або Find( ).

Приклад 4.5. Станція технічного обслуговування автомобілів здійснює зарядку акумуляторів і використовує для цього електроліт у кількості 1000 літрів у місяць. Замовлення на нову поставку електроліту обходиться станції у 100 грн. Вартість зберігання одного літра електроліту протягом місяця дорівнює 2 грн., а питомі втрати від його дефіциту – 10 грн. за один літр. Статистичні дані свідчать про те, що попит у період поставки є випадковою величиною, рівномірно розподіленою у інтервалі (a, b) літрів, де

Визначимо оптимальну стратегію управління запасами:

 оптимальний обсяг поставки і оптимальний щоденний запас електроліту на складі такі, щоб можливі витрати на їх зберігання і збитки від дефіциту були б мінімальні;

 кількість замовлень і інтервал часу між послідовними замовленнями.

Використовуючи прийняті в моделі позначення маємо:

Q

t

= 1000 літрів у місяць;

f(x) =1/ a,

с₁ = 100 грн. за подачу замовлення;

с₂ = 2 грн. за один літр у місяць;

с₃ = 10 грн. за один літр.

Алгоритм реалізації моделі

 задаємо вхідні дані моделі;

 записуємо вирази для щільності рівномірного розподілу і визначаємо математичне сподівання попиту;

 записуємо вирази для відповідних інтегралів, і інтегруючи, одержуємо їх значення у символьному вигляді;

 записуємо вираз для математичного сподівання витрат G(q, h);

 визначаємо екстремальні значення величин q і h. Для визначення екстремальних значень застосуємо два алгоритми.

Алгоритм 1: Система рівнянь задана у неявному вигляді

 задаємо початкові значення шуканих величин

 у блоці розв’язання Given записуємо систему рівнянь відносно змінних прирівнюючи до нуля частинні похідні від функції відповідно по ;

 розв’язуємо систему рівнянь відносно величин за функцією Mathcad і знаходимо екстремальні значення

Алгоритм 2: Система рівнянь задана у вигляді формул (4.50), (4.51)

 записуємо формулу (4.50) для q як функцію від і відповідне співвідношення для визначення за формулою (4.51);

 задаємо початкові значення шуканих величин

 у блоці розв’язання Given записуємо систему рівнянь відносно змінних і розв’язуємо її за допомогою функції

 визначаємо мінімальне значення функції при

 знаходимо значення величин

Проводячи обчислення за цим алгоритмом, одержуємо оптимальне значення обсягу поставки q₀, оптимальну точку замовлення , а також кількість замовлень і інтервал між замовленнями .

Алгоритм у Mathcad

Алгоритм 1

Given

Система рівнянь відносно і її розв’язок

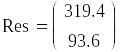
Оптимальний обсяг поставки і точка замовлення

Алгоритм 2

Вираз для як функції від

Система рівнянь відносно і її розв'язок

Оптимальний обсяг поставки і точка замовлення

_{Мінімальне значення витрат}

Коментар. Оптимальний обсяг поставки літрів, точка замовлення літри, кількість замовлень у рік рази, інтервал між послідовними замовленнями дня. Мінімальне значення очікуваних витрат грн. ▲