4.5. Модель системи управління запасами з попитом, розподіленим за нормальним законом

При великому попиті пуассонівський розподіл кількості замовлень в моделях управління запасами можна апроксимувати нормальним розподілом. У таких випадках змінні вважаються неперервними величинами. Зауважимо, що при великих значеннях математичного сподівання розподіл Пуассона наближається до нормального розподілу з математичним сподіванням і дисперсією У даній моделі ми не будемо обмежуватись умовою тому що далі буде розглянутий випадок змінних термінів поставок. У цьому параграфі будемо вважати, що час поставок постійний. Знявши обмеження і покладаючи незалежним параметром, одержимо рівняння, які одночасно можна використовувати при випадкових термінах поставок.

Фіктивний рівень запасу може приймати тепер будь-які значення від до а не тільки цілі значення Імовірність того, що фіктивний запас знаходиться у інтервалі дорівнює оскільки у пункті 4.3 було показано, що ймовірність перебування системи у стані дорівнює Це випливає із загальної методики апроксимації розподілу Пуассона нормальним розподілом. Фіктивний рівень запасу змінюється від до Але оскільки у практичних випадках різниця від заміни цього інтервалу інтервалом буде невелика, то

Замість розподілу Пуассона для попиту за час поставки будемо використовувати нормальний розподіл

де математичне сподівання попиту за час поставки. Далі будемо використовувати той факт, що Тоді для рівня наявного запасу в момент можна визначити щільність імовірності у вигляді

(4.27)

Аналогічно для числа врахованих замовлень в момент щільність імовірності розподілу буде мати такий вигляд

(4.28)

Тоді ймовірність дефіциту дорівнюватиме

(4.29)

Для перетворення деяких математичних виразів нам будуть потрібні формули

(4.30)

(4.31)

Використовуючи першу із цих формул, одержимо

Таким чином, середня кількість замовлень за рік складе

, (4.32)

де

Математичне сподівання кількості врахованих замовлень у будь-який момент часу дорівнює

Зробимо перетворення наступного співвідношення, застосовуючи формулу (4.31):

Тепер формула для буде мати вигляд

(4.33)

де

Залишається визначити середній рівень запасу в момент

(4.34)

Тепер, враховуючи (4.32)–(4.34), можна визначити середні річні витрати як

(4.35)

Оптимальні значення будуть розв’язком системи рівнянь

(4.36)

У випадках, коли членами можна знехтувати, рівняння (4.36) мають вигляд

(4.37)

Для визначення оптимальних значень величин можна застосувати алгоритм, що зводиться до розв’язання системи рівнянь у блоці розв’язку у Mathcad.

Коли а член малий, вплив на коефіцієнт витрат утримання запасів незначний, співвідношення (4.35) і (4.37) будуть мати вигляд (4.6).

При використанні точного виразу для функції витрат, одержаного у даному розділі, алгоритм розрахунків дещо ускладнюється. З урахуванням членів функція витрат не завжди буде опуклою. Ця обставина ускладнює пошук оптимальних значень На практиці ці члени використовуються не часто, у наслідок того, що вони незначно впливають на точність результатів.

Алгоритм реалізації моделі

 задаємо вхідні дані моделі ;

 записуємо функцію щільності ймовірності нормованого нормального розподілу і його функцію розподілу , а також функції і функцію витрат ;

 для визначення оптимальних значень знаходимо глобальний мінімум функції Для цього масив значень функції перетворюємо у відповідну матрицю і за допомогою оператора Mathcad знаходимо в ній мінімальний елемент , який визначає глобальний мінімум функції ;

 визначивши значення глобального мінімуму функції знаходимо екстремальні точки , які відповідають мінімуму. Для їх визначення застосовуємо класичний алгоритм: знаходимо частинні похідні функції по Прирівнюючи їх до нуля, одержуємо систему двох рівнянь відносно невідомих ;

 у блоці Given розв’язуємо систему рівнянь і знаходимо точки мінімуму функції ;

 визначаємо гарантійний запас ;

 визначаємо мінімальне значення функції витрат

Приклад 4.3. Система управління запасами характеризується такими параметрами: попит на товари описується розподілом Пуассона з параметром одиниць у рік. Час поставки постійний і дорівнює року. Інші параметри задачі мають такі значення: грош. од., грош. од., долара, долара, долара на одиницю товару.

Використовуючи стратегію , визначимо оптимальні значення розміру партії поповнення запасу , рівня подачі замовлення та рівень гарантійного запасу за критерієм мінімуму очікуваних витрат на поставки продукції, утримання запасів і втрат у наслідок дефіциту.

Алгоритм у Mathcad

_{Вхідні дані}

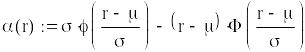
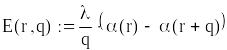
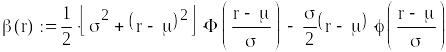
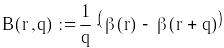
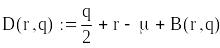
_{Цільова функція (загальні витрати системи)}

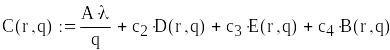
Перетворення аргументів функції у відповідні елементи матриці

Фрагмент матриці

Мінімальне значення цільової функції

Індекси мінімального елемента матриці

Оптимальні значення величин

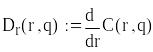
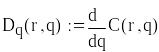
Функціональні характеристики системи:

 імовірність дефіциту

 середня кількість врахованих замовлень за рік

 математичне сподівання кількості втрачених замовлень

 середній рівень наявного запасу

Коментар. Оптимальна стратегія управління запасами у даній системі, передбачає розмір замовлення у кількості од. товару. Оптимальна точка подачі замовлення відповідно дорівнює одиницям. Очікуваний попит за час поставки і гарантійний запас відповідно дорівнюють і од. товару.

Як зазначалось раніше, використовуваний алгоритм дозволяє знайти оптимальні значення , коли функція є строго вгнутою. Отже у даній задачі

функція має абсолютний мінімум, який визначається точками . ▲