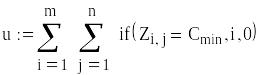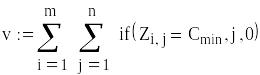4.4. Частинний випадок точної моделі

У більшості практичних задач величини , які входять у , нехтовно малі. Вони повинні враховуватись тільки у тих випадках, коли є суттєво велика ймовірність того, що попит за час поставки перевищує Якщо це так, то після поставки поповнення будуть, як і раніше, залишатись невиконані замовлення із числа врахованих до поставки, тобто поповнення буде недостатнім для задовільнення усіх врахованих замовлень. Якщо витрати по обліку не будуть нехтовно малі, не доцільно допускати таку кількість врахованих замовлень, щоб їх не можна було задовільнити однією поставкою. На практиці можна знехтувати членами і тоді витрати дорівнюватимуть

(4.26)

Якщо є найменшими значеннями , які мінімізують то необхідно щоб виконувались умови

Таким чином, є найбільше значення для якого і є найбільше значення для якого .

Якщо визначити із (4.26), то

Якщо то

Для обчислення , знайдемо величини і . Із виразів для маємо

Таким чином,

і якщо то

Хоча алгоритм реалізації даної моделі складніший ніж наближеної, застосування сучасних комп’ютерних технологій, зокрема, Mathcad-технології, дозволяє досить просто визначити оптимальні значення її параметрів.

Алгоритм визначення оптимальних значень

 задаємо вхідні дані моделі

 записуємо функції

а також функцію витрат

 знаходимо за формулою Уілсона і визначаємо найбільше для якого

 задаємо діапазони можливих значень . З метою зменшення області пошуку оптимальних значень значення вибираємо близькими до визначеного на попередньому кроці, значення близькими до Перетворюємо двовимірний масив значень функції у матрицю . Індекси елементів масиву визначаємо за допомогою відповідних лічильників;

 визначаємо розмірності матриці і її мінімальний елемент ;

 визначаємо індекси і елемента матриці і за ними визначаємо оптимальні значення

 визначаємо гарантійний запас

 визначаємо мінімальне значення функції витрат . Збіг цього значення з попереднім , визначеним за допомогою функції , є підтвердженням правильності знаходження оптимальних значень . Зауважимо, що функція може бути і не строго вгнутою, тобто може мати і локальні мінімуми. Але даний алгоритм вірний, тому що мінімум, знайдений за допомогою функції є глобальним.

У [9] наведений ітераційний алгоритм визначення оптимальних значень Хоча цей алгоритм досить простий і дозволяє знайти мінімум цільової функції, але він не гарантує, що цей мінімум є глобальним. Це пояснюється тим, що ітераційна процедура з початковим значенням , визначеним за формулою Уілсона, не гарантує збіжність розв’язку саме до глобального мінімуму.

Приклад 4.2. Фірма продає у середньому у рік 50 вінчестерів для комп’ютерів. Процес попиту на ці вироби наближено можна вважати пуассонівським. Витрати по замовленням і поставкам складають 100 грош. од. на кожний замовлення. Вартість кожного вінчестера в середньому дорівнює 50 доларам незалежно від розміру замовлення, коефіцієнт витрат утримання запасу дорівнює Невиконані замовлення враховуються і витрати обліку оцінюються у 50 грош. од. на одне замовлення плюс 500 грош. од. штрафу за дефіцит одиниці товару протягом року. Термін поставки у середньому складає біля 0,4 роки. Фірма використовує систему оперативного контролю інформації. Тому вона вирішила застосувати систему подачі замовлень на поповнення запасів при зниженні їх рівня нижче певного значення.

Обчислимо оптимальну точку подачі замовлення і його оптимальний розмір

Алгоритм у Mathcad

_{Вхідні дані}

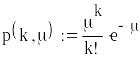
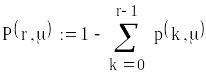
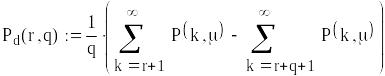
_або

Цільова функція (загальні витрати системи)

Оптимальний рівень запасу за формулою Уілсона

Критичне значення при якому змінює знак з мінуса на плюс (точка мінімуму функції визначаємо із наступної таблиці

r
5		-7.7
26		-2.4
27		1.6
28		4.4

Критичне значення

Перетворення масиву значень функції у матрицю .

Фрагмент матриці

Індекси мінімального елемента матриці , який дорівнює

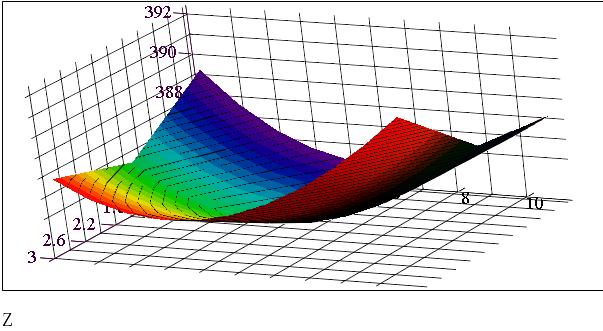
Рис. 4.3. Графік функції

Оптимальні значення які дають мінімум функції витрат :

Функціональні характеристики системи:

 гарантійний запас

 імовірність дефіциту

 середня кількість врахованих замовлень за рік

 середня кількість втрачених замовлень

 середній рівень наявного запасу

Коментар. Оптимальна стратегія управління запасами у даній системі полягає у тому, що розмір замовлення складає одиниці товару, а оптимальна точка його подачі, обчислена за фіктивним рівнем запасу, дорівнює одиниць. Оскільки очікуваний попит за час поставки дорівнює одиниць, то гарантійний запас складе 4 одиниці товару. Мінімальне значення загальних річних витрат при цьому складе грош. од.. ▲