РОЗДІЛ 4. СТОХАСТИЧНІ МОДЕЛІ СИСТЕМ

ОПЕРАТИВНОГО УПРАВЛІННЯ ЗАПАСАМИ

У цьому розділі, вивчаються моделі систем управління запасами, які називаються (q, r)-моделями. У таких моделях кожний раз при зниженні рівня запасів (наявного запасу, чистого запасу, наявного запасу плюс обсяг замовлення на поповнення, який називають фіктивним рівнем запасу) до певного рівня подається замовлення на партію розміру Задача аналізу таких систем полягає у визначенні оптимального розміру партії , яка замовляється, і рівня запасу r, який називається точкою подачі замовлення. Точка замовлення визначає момент часу подачі замовлення.

Для здійснення цієї стратегії управління потрібно, щоб стан складської системи перевірявся після кожної нової поставки. Таким чином, застосування -моделі управління запасами потребує введення оперативної інформації.

Друга процедура управління запасами передбачає два рівня запасів Якщо при надходження замовлень рівень запасу знижується до , то подається замовлення на поповнення запасу розміром Таку процедуру управління називають rR--стратегією, а модель оперативного управління запасами, яка використовує цю стратегію, (r, R)-моделлю. Модель представляє частинний випадок -моделі при

4.1. Наближена модель системи з обліком невиконаних замовлень

У цьому розділі розглянемо -модель із обліком невиконаних замовлень, а у наступному вивчимо моделі систем з втратами невиконаних замовлень. Будемо припускати, що розглядувана система складається із одного складу. Треба визначити оптимальні розміри партій , що замовляються, і рівень запасів при якому подається замовлення (точку замовлення поставки на поповнення запасу). Вибір оптимальних значень буде проводитись за критерієм середніх річних витрат. Будемо також припускати, що:

1. Вартість одиниці запасів 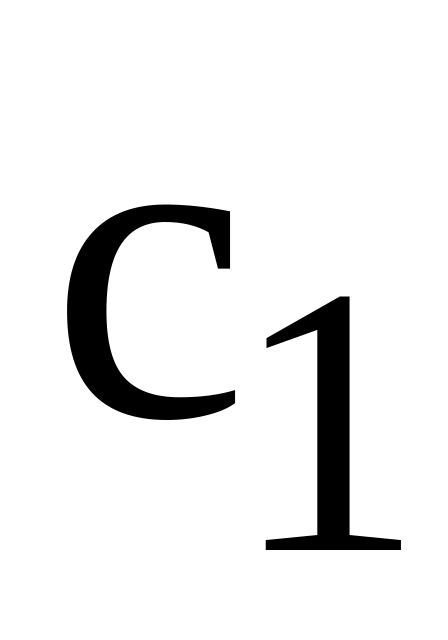не залежить від розміру партії

2. Витрати по врахуванню невиконаних замовлень у розрахунку на одиницю запасів не залежать від тривалості дефіциту і дорівнюють .

3. У системі є не більше одного невиконаного замовлення.

4. Витрати, пов’язані із роботою системи обробки інформації, не залежать від

5. В моменти подачі замовлень на поповнення запасів у системі не буде невиконаних замовлень із числа врахованих.

Припущення 3 означає, що якщо в момент досягнення рівня подачі замовлення на поповнення запасу відсутні невиконані замовлення, то фіктивний запас (наявний запас плюс розмір замовлення мінус враховані замовлення) дорівнює чистому запасу (наявному запасу мінус обсяг врахованих замовлень).

Таким чином, вибір точки замовлення не залежить від того, чи ведеться розрахунок по фіктивному, чи по чистому запасу. Додатково припустимо, що рівень подачі замовлень (який розраховується за фіктивним рівнем і чистим запасом) додатний. Це припущення майже завжди виконується на практиці, тому що не має смислу затримувати подачу замовлення, якщо вже є невиконані замовлення.

Припущення 5 означає, що в моменти подачі замовлень на поповнення запасу фіктивний рівень запасів дорівнює наявному, як показано на рис. 4.1. У розглядуваній вище системі точка замовлення може бути визначена і за наявним, і за чистим, і за фіктивним рівнем запасів. При використанні наявного запасу треба припустити, що обсяг поповнення буде достатнім для задовільнення усіх врахованих замовлень і створення рівня наявного запасу, що перевищує рівень замовлення на поповнення (точку замовлення). Якщо таке перевищення коли-небудь не досягається, то у системі будуть накопичуватись невиконані замовлення. Якщо точка замовлення визначається за фіктивним рівнем, то умова 3 гарантує, що наявний запас після поповнення буде перевищувати рівень, який відповідає точці замовлення.

Як і раніше, будемо називати циклом інтервал між двома послідовними подачами замовлень на поповнення або між двома послідовними поставками. Але тепер протягом кожного циклу система може і не зберігати в точності характер функціонування. Навіть сам цикл тепер є випадковим. Однак фіктивний рівень запасу буде кожний раз змінюватись від до

Розглянемо складові середніх річних витрат: вартість подачі замовлень, витрати утримання запасів і витрати по врахуванню невиконаних замовлень. У наслідок припущення 1 вартість самих запасів товарів можна не враховувати, тому що середня річна вартість поставок не залежить від і вартість одиниці запасів не залежить від Розглянемо неперервний варіант моделі. Не викликає труднощів видозмінити модель на випадок, коли величини і попит дискретні.

Введемо позначення:

обсяг поставки;

точка подачі замовлення на поповнення запасу;

середній рівень чистого запасу;

щільність розподілу попиту Х в момент часу ;

середня інтенсивність попиту, яка за припущенням, не залежить від

вартість подачі замовлення;

вартість одиниці запасу;

коефіцієнт витрат утримання запасів;

середні витрати утримання одиниці запасів;

витрати по обліку невиконаних замовлень.

Треба визначити оптимальні значення

Оскільки, річний попит дорівнює а замовлення подається кожний раз після надходження замовлень, середні річні витрати на поповнення замовлень будуть дорівнювати Середні річні витрати утримання запасів дорівнюють добутку на середню величину запасу за рік. За означенням, чистий запас дорівнює наявному запасу мінус обсяг врахованих замовлень, тобто різниці двох випадкових величин. Тому математичне сподівання чистого запасу дорівнює різниці математичних сподівань наявного запасу і обсягу врахованих замовлень. Для визначення середньої величини запасу за рік необхідно проінтегрувати за часом середній наявний запас, або, що те ж саме, середній чистий запас плюс середній обсяг врахованих замовлень. Середній обсяг врахованих замовлень буде значно відрізнятись від нуля тільки на малих інтервалах часу, при умові, що витрати на облік замовлень високі. Тому при інтегруванні ця добавка буде незначна, і можна вважати, що середнє число врахованих замовлень нехтовно мале, а середній наявний запас можна прирівняти середньому чистому запасу.

За означенням, середній рівень чистого запасу в момент поставки поповнення дорівнює гарантійному запасу а зразу ж після поставки розміром q одиниць буде Тому на початку циклу середній рівень чистого запасу дорівнює , а у кінці Отже середня кількість запасів за рік буде дорівнювати

Для подальшого опису моделі зручно виключити замінивши його на Точка подачі замовлення на поповнення однакова і дорівнює при обчисленні через наявний запас і через чистий запас. За цикл виконується лише одне замовлення на поповнення. Тому для часу поставки , при умові, що попит за цей час дорівнює Х, чистий запас в момент поставки дорівнює а середнє значення чистого запасу, усереднене по всім значенням Х для заданого буде дорівнювати

Якщо час поставки постійний, то цим співвідношенням визначається гарантійний запас. Припустимо, що час поставки випадковий і має щільність імовірності Тоді середнє значення буде дорівнювати

де

– безумовний розподіл попиту за час поставки. Тому для середнього рівня чистого запасу можна записати такий вираз

де

– середній попит за час поставки, а якщо час поставки постійний і дорівнює або визначається за наведеною вище формулою, якщо час поставки випадковий і має щільність імовірності Тому середні річні витрати на утримання запасу дорівнюють

(4.1)

Визначимо тепер середні річні витрати обліку замовлень. Середнє число врахованих замовлень за рік дорівнює добутку середнього числа врахованих замовлень за цикл на середнє число циклів за рік, тобто добутку на середнє число врахованих замовлень за цикл . Якщо попит за час поставки дорівнює Х, то число врахованих замовлень дорівнюватиме

Середнє число врахованих замовлень за період дорівнює

(4.2)

де безумовна щільність розподілу попиту за час поставки, а

– інтегральний розподіл попиту за час поставки.

Таким чином, середні річні витрати обліку невиконаних замовлень визначаються як

(4.3)

За знайденими складовими загальні середні річні витрати дорівнюють

(4.4)

Зауважимо, що у цей вираз не включена вартість самих запасів і витрати, пов’язані з роботою інформаційної системи обробки даних.

Потрібно визначити значення і які мінімізують загальні витрати системи Якщо оптимальні значення задовольняють нерівностям то вони повинні бути розв’язком рівнянь

(4.5)

.

Ці рівняння зручно представити у вигляді

, (4.6)

Часто виявляється необхідним оцінити чисельно для заданих значень Якщо припустити, що є нормальним розподілом з математичним сподіванням (середнім обсягом попиту за час поставки) і середнім квадратичним відхиленням тобто

,

то будемо мати співвідношення

,

де є щільність нормованого нормального розподілу, а – його додаткова функція розподілу.

Величина у цьому випадку дорівнюватиме

4.7)

Формула (4.4) для функції середніх річних витрат з урахуванням (4.7) прийме вигляд

(4.8)

Функції можна обчислити за допомогою функцій Mathcad які визначають щільність імовірності і функцію нормального розподілу.