6. Способи усунення тренда. Моделі згладжування для часових рядів, що не мають тренда: комбінована модель.

. Для того, щоб в цьому випадку можна було застосувати модель, призначену для процесів, що не мають тренда, можна поступити одним з наступних двох способів.

Спосіб 1. Розглянемо різниці або частки початкових даних. Таким чином, якщо є ряд даних Y₁, Y₂, ..., Y_n, то розглядається ряд: Δ2_{, ...,} Δn, де Δt = Y_t – Y_t-1, або ряд р2, ..., рn, де

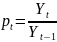(4.3)

Якщо менеджер вважає, що можна нехтувати зміною в змодельованих квартальних темпах зростання, то він може розглядати р2, ..., рn як ряд, що не має тренда, і застосувати до нього наївну або будь-яку іншу модель, призначену для рядів, що не мають тренда.

Спосіб 2 полягає в розгляді залишків лінійної регресії і є одним з найчастіше використовуваних методів усунення тренда. Його називають методом детрендалізації.

Якщо коефіцієнт b2 лінійного рівняння регресії для ряду еi має нулі в перших чотирьох десяткових розрядах, то він може вважатися рівним нулю. Тепер можна побудувати модель для ряду без тренда для залишків е_і, потім знайти відповідне змодельоване значення e_k при k > 17, і додати його до відповідного значення тренда. Оскільки наївна модель припускає, що e_t-1≈ e_t, то її слід застосовувати у тому випадку, коли коефіцієнт кореляції r(e_t-1, e_t ) при t = 2, ..., n, позитивний і значно відрізняється від нуля. У такому разі говорять, що в моделі лінійної регресії є позитивна автокореляція першого порядку. Існує спеціальний тест (тест Дарбіна-Уотсона) на наявність автокореляції першого порядку.

Прогноз визначається шляхом додавання змодельованої помилки е₁₉ до відповідного значення тренда.

7. Визначення початкових значень моделі.

Для обчислення значення моделі у момент t ми повинні знати її значення в попередній момент t - 1, то перед нами встає задача визначення початкових значень моделі (в даному випадку у момент часу t = 1).

Найпростіший спосіб – узяти як початкове значення або .

У сучасному прогнозуванні досить поширений метод прогнозування назад (backcasting). Наприклад, можна розглянути модель, подібну моделі (4.7), з тією лише різницею, що рекурсивність здійснюється у зворотному напрямі:

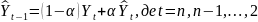(4.10)

(4.11)

Початкове значення можна взяти відповідно до досвіду і розуміння прогнозистом процесу.

Найкращий спосіб визначення початкових значень, особливо для прогнозистів, що починають, полягає у виборі опції, «автоматично» присутньої у всіх статистичних пакетах.

5. Моделі згладжування з трендом: модель Холта, модель Брауна.

Модель Холта.

Застосуємо модель експоненціального згладжування до різниць 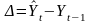, з константою згладжування, рівною 1 – β, де 0 ≤ β < 1. При цьому значення моделі позначимо як Т_t і назвемо їх значеннями тренда. Таким чином, одержуємо перше рівняння Холта:

(4.12)

друге рівняння Холта:

(4.13)

Побудова моделі зводиться до трьох основних етапів.

1. Ухвалюють рішення щодо величин параметрів моделі α і β. Якщо немає особливих переваг, то оптимальні значення α і β визначають як завжди, виходячи з мінімізації MSE.

2. Визначають початкові значення і T_t. Що ж до T_t., то можна узяти Т₁ = (Δ₂ + Δ₄ )/2.

3. Поперемінно знаходять і T_t. При цьому спочатку обчислюють і лише потім – T_t.

Модель подвійного експоненціального згладжування з трендом (модель Брауна – Brown's double exponential smoothing model with trend).

модель Брауна визначається наступною формулою:

(4.15)

Прогноз на h кроків вперед визначається формулою:

(4.16)