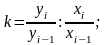Ex post як імітація процесу прогнозування. Алгоритм ex post прогнозування. Оцінка помилок ex post прогнозів.
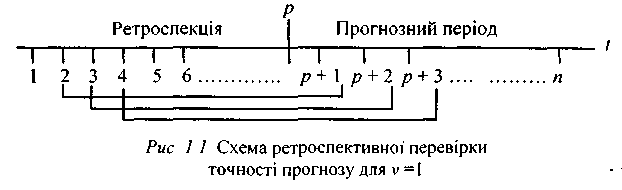
Найбільш поширене ретроспективне оцінювання прогнозу, тобто оцінювання прогнозу для минулого часу (ex-post прогноз). Процедура перевірки така. Динамічний ряд поділяється на дві частини: перша — для t= 1,2,3, ...,p — називається ретроспекцією (передісторією), друга — для t=p + 1, p + 2, p + 3, ..., p +(n —р) — прогнозним періодом.
За даними ретроспекції моделюється закономірність динаміки і на основі моделі розраховується прогноз Yp+v, де v — період упередження. Ретроспекція послідовно змінюється, відповідно змінюється прогнозний період, що унаочнює рис. 1.1 (для v = 1).
Еx post – один з найнадійніших методів при виборі моделі прогнозування. При цьому особливу увагу слід звертати на останні значення моделі. Стабільність коефіцієнтів моделі, разом з іншими характеристиками, які вказують на достатньо високу точність (R2, MAD і МАРE), говорить на користь вибраної моделі.
Нижче ми приводимо докладний алгоритм ex post прогнозування.
Алгоритм ex post прогнозування:
1. Знаходимо лінію регресії L для перших 13 значень.
2. З рівняння L визначаємо прогноз на 14-й квартал.
3. Порівнюємо одержаний прогноз з наявною інформацією за 14-й квартал. Знаходимо помилку.
4. Повторюємо пункти 1-3 послідовно для перших 14, 15 і 16 значень.
2. Поняття тенденції, умови існування та способи встановлення наявності тенденції. Прості методи екстраполяції тенденції: екстраполяція на основі аналітичних показників рядів динаміки.
Під тенденцією розуміють деякі загальні напрямки розвитку процесу (явища), довгострокову закономірність.
Основу екстраполяційних методів прогнозування складають динамічні ряди. Є ряд способів перевірки гіпотези про існування тенденції у динамічному ряду.
Один з найпростіших методів базується на порівнянні середніх рівнів ряду. Для цього динамічний ряд розбивається на дві, приблизно рівні частини за кількістю елементів. Кожна частина розглядається умовно як самостійна сукупність. Якщо динамічний ряд має певну тенденцію, то середні, які обчислені для кожної сукупності, повинні суттєво розрізнятися між собою. Якщо ж розходження будуть незначними, тобто випадковими, то динамічний ряд тенденції не має.
Для оцінки істотності відмінності між середніми значеннями двох динамічних рядів використовується t-критерій Стьюдента.
Розходження буде істотним, якщо розрахункове значення t-критерія Стьюдента (tp) буде не менше його табличного значення (tT).
Прості методи прогнозування на основі екстраполяції тенденції використовуються в управлінні виробництвом, оскільки мають ряд переваг.
До переваг простих методів слід віднести:
- достатньо простий апарат дослідження, що привертає до нього широке коло спеціалістів;
- можливість використання для виконання розрахунків портативних і нескладних обчислювальних засобів;
- швидкість виконання розрахунків в оперативному режимі;
- наявність відносно невеликого масиву інформації.
Наведемо основні аналітичні показники динамічного ряду, які використовуються у прогнозуванні:
а)
абсолютний приріст:1) ланцюговий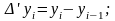
2) базисний
б)
середній абсолютний приріст
в)
коефіцієнт росту:1) ланцюгов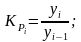ий
2)
базисний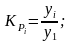
3) за весь період
г) коефіцієнт приросту Knp = kp - 1;
д)
середній коефіцієнт росту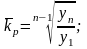
е)
середній коефіцієнт приросту
ж)
абсолютний розмір 1% приросту:1) ланцюговий
2) за
весь період
3) коефіцієнт випередження)