Стационарный тепловой анализ
Цель: Провести стационарный тепловой анализ конструкции пластины с отверстиями.
Тип анализа: Нелинейный тепловой расчет конструкции.
Тип конечного элемента: Двумерный твердотельный (Solid).
Тип граничных условий: Конвекция.
Возможности: Задание теплопроводности как функции температуры, построение графика температур и теплового потока.
Ход работы
3.1 Подготовка к тепловому расчету модели
Первым шагом мы определили тип проводимого анализа как тепловой расчет. Для этого в настройках главного меню выбрали Thermal. Единицы измерения температуры задали градусы Цельсия. Для этого выбрали Celsius в разделе Temperature Units для свойств материала.
3.2 Построение модели
Пользуясь интерфейсов среды ANSYS построили модель по заданному эскизу.
Рисунок 3.1 – Эскиз пластины с отверстиями
Определили свойства материала как изотропические с точки зрения температурного поля и теплопроводности. Задали теплопроводность как функцию температуры. Необходимо было задать четыре разных значения температуры и соответствующее значение теплопроводности для каждой из них.
Таблица 3.1 – Зависимость теплопроводности от температуры
Температура, С |
20 |
40 |
60 |
100 |
Теплопроводность, Вт/м С |
30 |
35 |
55 |
95 |
Плотность (Density) задали 7800 кг/м3 для материала модели.
Далее произвели разбивку модели на сетку конечных элементов. В качестве конечного элемента выбрали четырехузловой элемент Plane55.
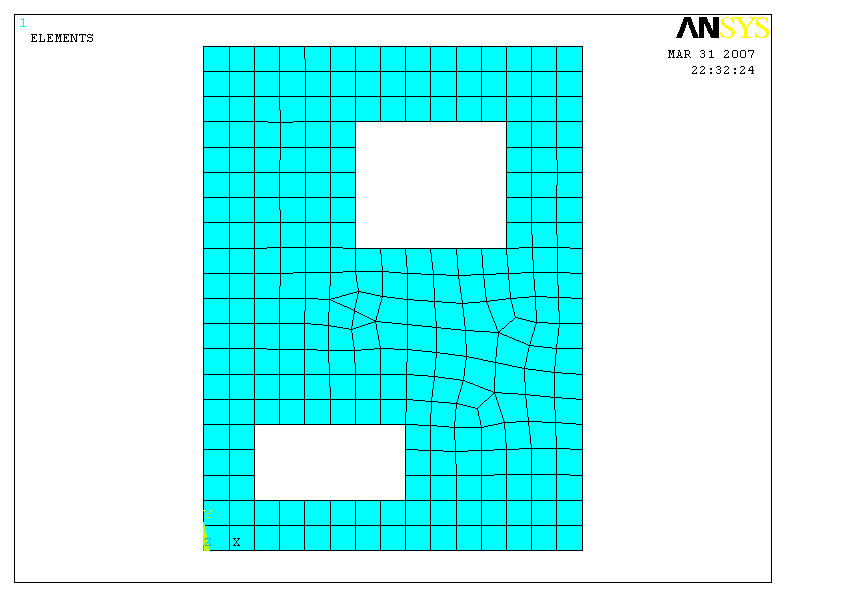
Рисунок 3.2 – Модель пластины с сеткой конечных элементов
Значение размера конечного элемента присвоили 0.01 и произвели разбивку всей площади модели.
3.3 Задание граничных условий
Т.к. расчет проводится температурный, граничными условиями являются значения температур в зонах модели. В качестве минимального и максимального значения мы присвоили комнатную температуру (20°С) верхней части модели (линия 1 на рис. 3.1) и 110°С нижней части (линия 2 на рис. 3.1).
Для этого задали температуру окружающей среды, которая непосредственно контактирует с выбранными линиями.
Main Menu → Solution → Define Loads → Apply → Thermal →
→ Convection → On lines… - использовали для выделения нужных нам линий и присвоили требуемые температуры.
Далее определили значение временного шага. Для этого в опциях шагов решения указали требуемое время и шаги (присовили параметрам значение 1):
Main
Menu →
2
Time and Substps
Следующим шагом было проведение расчета по заданным параметрам. Итогом расчета была полученная картина распределения температуры в теле модели.
Рисунок 3.3 – Распределение температур в модели пластины
Еще одни способом отображения результатов расчета являются графики. Мы построили графики температуры на заданном пути от точки А до точки В (рис. 3.1).
Main Menu → General Postproc → Path Operations → Define Path →
→ By Nodes… - выделили два узла в противоположных концах пластины, чтобы определить точки А и В. Назвали данный путь TEMP.
Далее определили, какие именно данные необходимо выводить награфике. Для этого в разделе Операций с путями выбираем DOF Solution и Temperature TEMP.
Получаем график распределения температур, выбирая заданное имя пути:
Main Menu → General Postproc → Path Operations → Plot Path Item→On Graph…
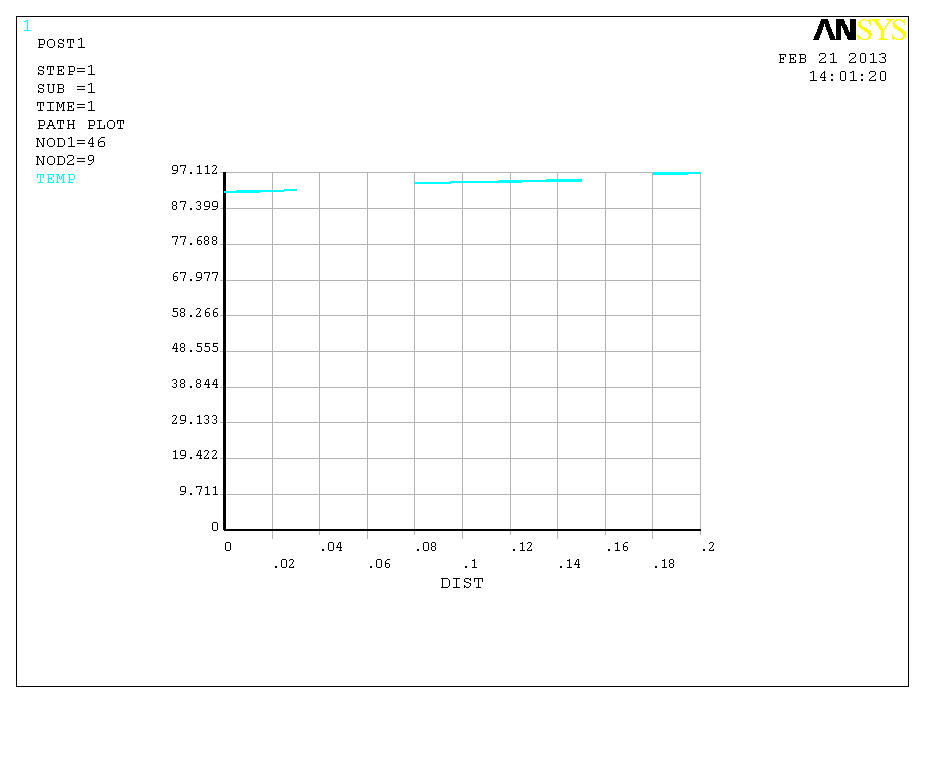
Рисунок 3.4 – График распределения температур по линии АВ
Следующим получили график величины теплового потока по заданному пути АВ.
Main Menu → General Postproc → Path Operations → Map Onto Path…
Выбираем PDEF Значения Flux&Gradient, Thermal Flux – TFSUM. Отображаем результаты в графике, выбирая TFSUM, чтобы получить только график изменения потока.
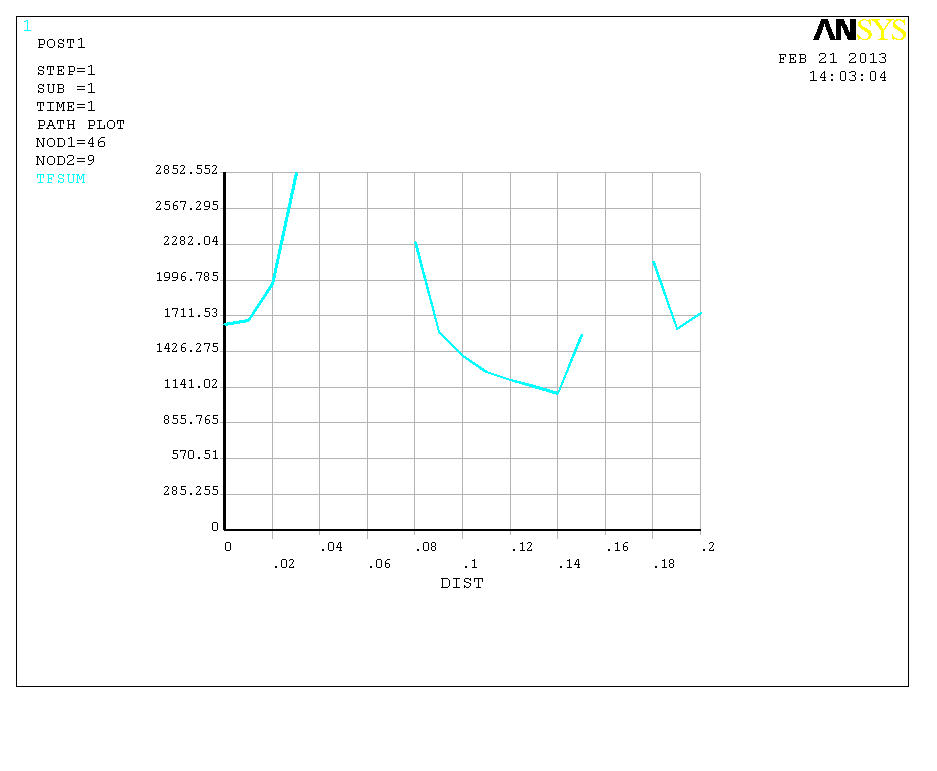
Рисунок 3.5 – График величины теплового потока в модели по линии АВ
Вывод: В ходе выполнения практической работы ознакомились со стационарным тепловым анализом. В качестве модели послужила прямоугольная пластина с двумя отверстиями. Результаты расчета были отображены в виде графиков величины теплового потока в модели и распределения температур по заданному пути от одного конца пластины до другого, а также в виде градиента температурной нагрузки в модели.
Практическая работа №4