3. Симметрия графика функции (четность, нечетность).

Область определения функции не симметрична относительно нуля, следовательно, это функция общего вида.

4. Исследуем поведение функции при .

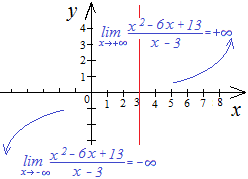
При уменьшении значений значения тоже уменьшаются .

При увеличении значений значения тоже увеличиваются .

, следовательно, горизонтальной асимптоты у графика нет.

5. Наклонные асимптоты.

Т.к. функция дробно-рациональная, ее график может иметь только одну наклонную асимптоту (двухстороннюю):

;

,

- наклонная асимптота графика функции.

6. Найдем интервалы монотонности (возрастания и убывания) функции и критические точки. Для этого

1. найдем производную первого порядка

2. приравняем ее к нулю

; ; ; .

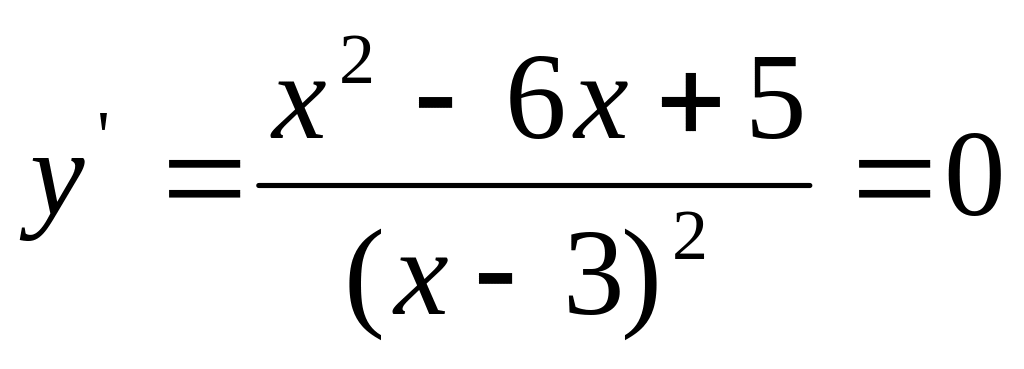
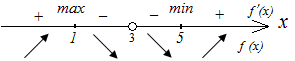
3. критические точки , и точку разрыва функции отметим на числовой прямой и определим знаки производной на полученных интервалах, сделаем выводы о монотонности функции.

;

;

При переходе через критические точки производная меняет знак, значит, эти точки являются точками экстремума. При у функции максимум, при - минимум. Вычислим значения функции в этих точках.

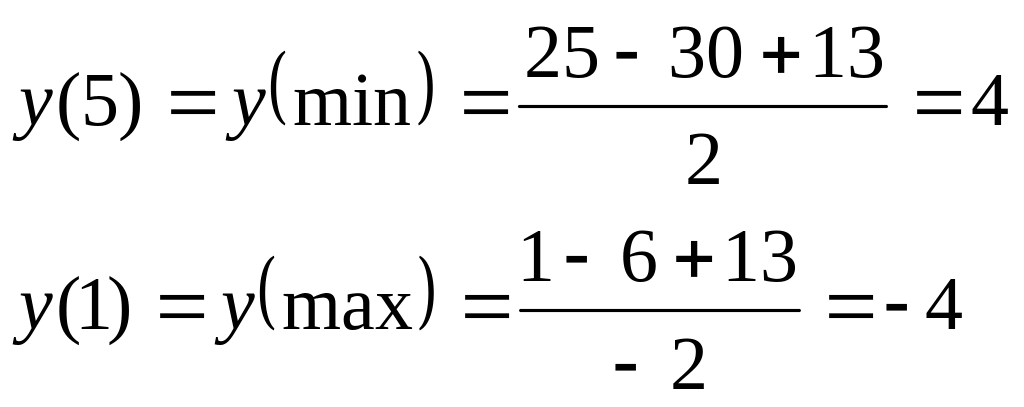
Соответствующие точки графика имеют координаты ,

7. Найдем интервалы выпуклости и вогнутости функции и проверим, имеет ли график функции точки перегиба. Для этого

1. найдем вторую производную функции

2. приравняем ее к нулю .

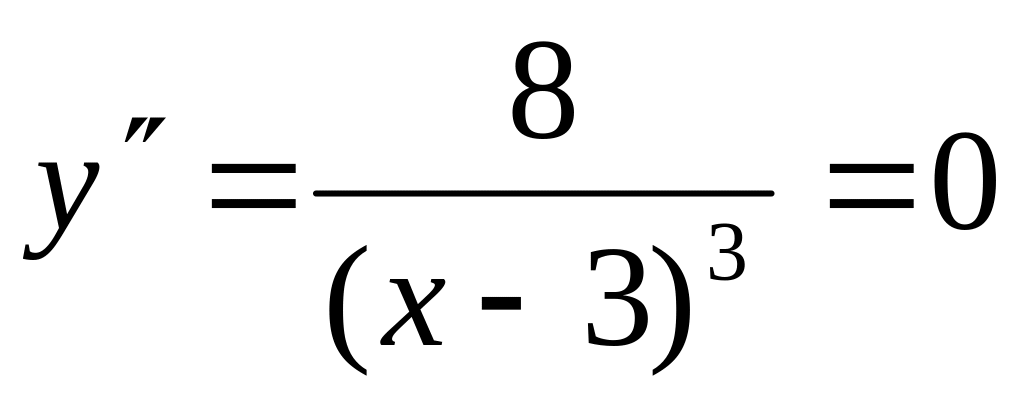Числитель дроби не может быть равен нулю. Значит, точки перегиба у графика нет.

3. Н 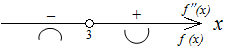айдем интервалы выпуклости и вогнутости. Для этого на числовой прямой отметим точку разрыва и определим знаки второй производной справа и слева от точки разрыва, сделаем выводы.

8. Занесем все полученные данные в таблицу.

	+	0	-	Точка разрыва	-	0	+
	-		-		+		+
		max				min
	Возрастающая выпуклая		Убывающая выпуклая		Убывающая вогнутая		Возрастающая вогнутая

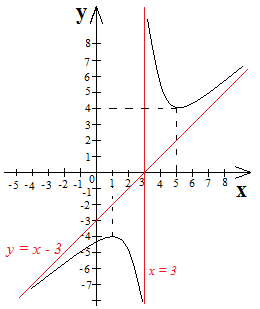
9. Нарисуем эскиз графика.

10. Отметим на плоскости точки экстремумов и точку разрыва. Начертим асимптоты графика. Покажем стрелками, куда будет направлен график функции при приближении его к асимптотам.

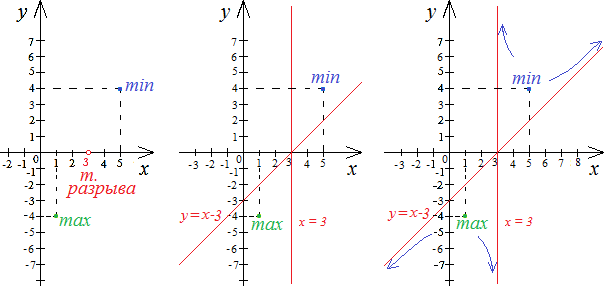
11. Построим график функции.