А
Оценка адекватности и надежности уравнения.
где у1 – фактические значения результативного показателя;
у0 – теоретические значения, найденные по уравнению.
При
моделировании экономических показателей
чаще всего допускается 5% ошибка. Модель
считается адекватной, а следовательно,
значимой если
.
Выбор наиболее оптимальной модели можно осуществлять на основе остаточного среднеквадратического отклонения (остаточной дисперсии):
где l – количество параметров уравнения.
Наилучшей будет та функция , у которой остаточная дисперсия меньшая.
Оценку надежности уравнения проводить по критерию Фишера, учитывая F–статистику:
где
-
среднее значение результативного
показателя.
Чем больше расчетная величина F–критерия, тем более значимая рассчитанная модель. Расчетное значение сравнивают с критическим значением, которое находят в таблицах распределения Фишера по ступеням свободы (l-1) и (n-l), задавая уровень значимости 0,05 (5% ошибка). Если, F>F табл, то уравнение считается надежным с вероятностью 0,95. В противоположном случае уравнение надежным не считается.
Пример:
- расчет для линейной функции:
У1 |
У0 |
У1 – У0 |
Апроксимация |
(У1 - У0)2 |
(У0 – У0сред)2 |
97 |
58,74 |
38,26 |
0,65 |
1463,83 |
25319,17 |
158 |
111,78 |
46,22 |
0,41 |
2136,29 |
11252,97 |
180 |
164,82 |
15,18 |
0,09 |
230,43 |
2813,24 |
195 |
217,86 |
22,86 |
0,10 |
522,58 |
0,00 |
220 |
270,90 |
50,90 |
0,19 |
2590,81 |
2813,24 |
292 |
323,94 |
31,94 |
0,10 |
1020,16 |
11252,97 |
383 |
376,98 |
6,02 |
0,02 |
36,24 |
25319,17 |
Всего |
1,56 |
8000,34 |
78770,76 |
||
F-табличное – 230,2
для параболической функции:
У1 |
У0 |
У1 – У0 |
Апроксимация |
(У1 - У0)2 |
(У0 – У0сред)2 |
97 |
652,13 |
555,13 |
0,85 |
308169,32 |
923463,34 |
158 |
743,82 |
585,82 |
0,79 |
343185,07 |
755647,72 |
180 |
972,69 |
792,69 |
0,81 |
628357,44 |
410124,97 |
195 |
1338,74 |
1143,74 |
0,85 |
1308141,19 |
75273,41 |
220 |
1841,97 |
1621,97 |
0,88 |
2630786,68 |
52381,48 |
292 |
2482,38 |
2190,38 |
0,88 |
4797764,54 |
755647,72 |
383 |
3259,97 |
2876,97 |
0,88 |
8276956,38 |
2712180,80 |
Всего |
5,95 |
18293360,62 |
5684719,43 |
||
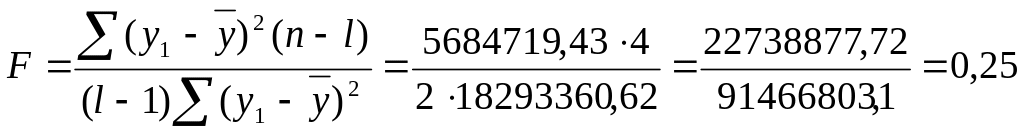
F-табличное – 19,25
для гиперболичной функции:
У1 |
У0 |
У1 – У0 |
Апроксимация |
(У1 - У0)2 |
(У0 – У0сред)2 |
97 |
291,14 |
194,14 |
0,67 |
37690,34 |
1134,34 |
158 |
264,40 |
106,40 |
0,40 |
11319,90 |
48,09 |
180 |
255,48 |
75,48 |
0,30 |
5697,23 |
3,92 |
195 |
251,02 |
56,02 |
0,22 |
3138,52 |
41,44 |
220 |
248,35 |
28,35 |
0,11 |
803,61 |
83,03 |
292 |
246,57 |
45,44 |
0,18 |
2064,34 |
118,70 |
383 |
245,29 |
137,71 |
0,56 |
18963,65 |
148,07 |
Всего |
2,45 |
79677,59 |
1577,60 |
||
F-табличное – 230,2
Таким образом, ни одна из представленных функций не достаточно надежна и не имеет практической значимости в силу больших расхождений между теоретическими и фактическими значениями результативного показателя.