1.2. Диамагнетизм; формула Ланжевена1

Явление диамагнетизма связано со стремлением электрических зарядов частично экранировать внутреннюю часть объема тела от действия внешнего магнитного поля. Из теории электромагнитных явлений нам известен закон Ленца, согласно которому при изменении магнитного потока, пронизывающего электрический контур, в контуре возникает индуцированный электрический ток такого направления, что создаваемое им магнитное поле противодействует исходному изменению магнитного потока. Магнитное поле, создаваемое индуцированным током, противоположно внешнему магнитному полю, а магнитный момент, связанный с этим током, и есть диамагнитный момент.

Обычное объяснение диамагнетизма атомов и ионов основывается на теореме Лармора, которая утверждает, что в магнитном поле Н движение электрона вокруг ядра в первом приближении по Н происходит так же, как и в отсутствие магнитного поля, но на него дополнительно накладывается общая прецессия с угловой частотой

(СГС). (1.28)

Если внешнее поле накладывается плавно, то движение во вращающейся системе координат будет выглядеть точно так же, как и в покоящейся системе до включения магнитного поля. Если средний электронный ток вокруг ядра был первоначально равен нулю, то включение магнитного поля приведет к тому, что появится конечный средний ток вокруг ядра. Установившийся ток эквивалентен определенному магнитному моменту, направление которого противоположно направлению внешнего поля (Рис. 1.4). Ларморова прецессия системы электронов эквивалентна электрическому току, выражение для которого (в электромагнитных единицах) имеет вид:

, (1.29)

где - заряд электронной оболочки иона,

-

число оборотов в единицу времени. Магнитный момент контура с током (см. введение) . Если контур круговой, то его площадь равна , где - радиус контура. Тогда индуцированный магнитным полем момент иона

, (1.30)

г

Рис. 1.4. Качественная картина, поясняющая появление электронного тока вокруг ядра иона в магнитном пол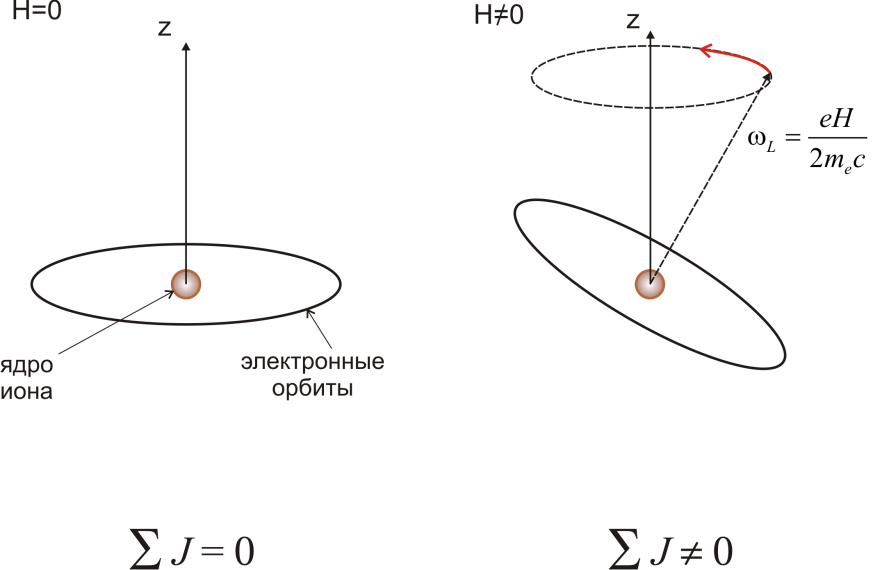е.

де - средний квадрат расстояния электронов от некоторой оси, проходящей через ядро параллельно полю (Рис. 1.5). Средний квадрат расстояния электронов от ядра:

. (1.31)

Если распределение заряда сферически симметрично, то и

Рис. 1.5. Расстояние электронов от ядра r и от оси, параллельной полю .

. (1.32)

Из (1.30) и (1.32), полагая, что число атомов на единицу объема равно , сразу получим диамагнитную восприимчивость (на единицу объема):

. (1.33)

Это и есть классический результат Ланжевена. Квантовомеханический вывод выражения для диамагнитной восприимчивости находится в согласии с классическим результатом.

Диамагнетизм – есть свойство всех материалов. В диэлектрических твердых телах диамагнитный вклад ионных остовов приближенно описывается формулой Ланжевена. Определение вклада электронов проводимости гораздо сложнее, в чем легко убедиться из рассмотрения, например, эффекта де Гааза-ван-Альфена.

Величины диамагнитной восприимчивости лежат в пределах . Диамагнитная восприимчивость всегда отрицательна, так как . Температура не входит явно в выражение для диамагнитной восприимчивости. Наблюдаемое в опытах малое изменение с температурой может быть объяснено слабой зависимостью от температуры.

Задача вычисления диамагнитной восприимчивости изолированного атома сводится к расчету величины для распределения электронов в атоме. Сам характер распределения может быть определен из квантовомеханических соображений, но точное решение этой задачи возможно только для атома водорода и изоэлектронных ионов (т.е., ионов, имеющих один валентный электрон на орбите).

Атом водорода. Так как в основном состоянии волновая функция атома водорода имеет вид

,

где

см

(радиус Бора), то

.