Формула Бейза: вероятность причин, гипотез, или обратные или предсказательные вероятности

Формула Бейза устанавливает связь между условными вероятностями и 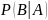для двух случайных событий A и B:

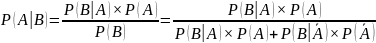
Другая интерпретация. Вероятность можно назвать априорной вероятностью события A, т.е. вероятностью этого события до осуществления события B. Условную вероятность можно назвать апостериорной вероятностью события A, т.е. вероятностью этого события после осуществления события B. При такой интерпретации формула Бейза устанавливает связь между априорной и апостериорной вероятностями события A (относительно осуществления или неосуществления события B).

Формула Бейза в терминах оддов и правдоподобий

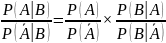
Условные вероятности и 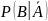принято называть правдоподобиями, а их отношение – отношением правдоподобий (LR – от англ. Likelihood Ratio):

Тогда в обозначениях для отношения правдоподобий и априорных и апостериорных оддов (шансов за и против) формула Бейза имеет вид:

Это означает, что апостериорные (т.е. после того как произошло событие B) одды (шансы за и против) события A равны его априорным оддам, умноженным на отношение правдоподобий LR:

Апостериорные шансы = Априорные шансы × Отношение правдоподобий

В теории проверки статистических гипотез событие A несет смысл проверяемой гипотезы, обычно называемой нулевой гипотезой H₀, а противоположное событие несет смысл альтернативной гипотезы H₁. Тогда соответствующее отношение правдоподобий принято называть бейзовым фактором BF₀₁. Подстрочный индекс 01 (читается как «ноль-один») означает, что сравнивается нулевая гипотеза с альтернативной. Обратная величина для сравнения альтернативной гипотезы с нулевой будет иметь подстрочный индекс 10: (читается как «один-ноль»).

Популяция и выборка Определение понятия «популяция»

В медицине и в эпидемиологии термин Популяция является калькой с английского population - синоним статистического понятия «генеральная совокупность», т.е. совокупность индивидуумов, из которой отбирается выборка, и на которую распространяются результаты, полученные для этой выборки.

Популяция может представлять собой все население (в эпидемиологических исследованиях) данной местности или данной этнической принадлежности, или же состоять из пациентов с определенным заболеванием. Таким образом, можно говорить об общей популяции или популяции пациентов с конкретным заболеванием.

Важнейшее требование к популяции и к выборке - однородность4

Отправной точкой (пусковым, стартовым моментом) в статистическом анализе является обобщение информации, полученной от ограниченного числа различающихся единиц наблюдения (выборка). Сведения (выводы), получаемые на основе такого объединения распространяются на все объекты такой природы (домысливаемая генеральная совокупность).

Получаемые таким путем выводы будут надежными, только если мы уверены, что наблюдаемые единицы являются однородными (принадлежат одной и той же генеральной совокупности, имеют одно и то же вероятностное распределение).

Однородность (гомогенность) выборки является фундаментальным, центральным, ключевым для всех последующих выводов и предсказаний.

Перед тем как подвергать исходные данные основной статистической обработке, исследователь должен ответить на вопрос: Правомерно ли объединение имеющихся в его распоряжении порций (выборок) в один общий массив или же каждая из порций имеет свою специфику и, следовательно, и обрабатывать их надо по отдельности?

В терминах Математической Статистики этот вопрос сводится к проверке однородности (гомогенности), т. е. к выяснению, можно ли считать имеющиеся порции данных выборками из одной и той же генеральной совокупности.

Основные схемы формирования выборок в диагностических исследованиях

Общепопуляционное (population-based) или поперечно-срезовое одномоментное (cross-sectional) формирование и исследование выборки

Упрощающие предположения:

1.Исходно предполагается, что обследуемая (изучаемая) популяция людей является практически однородной по всем свойствам (признакам), за исключением наличия диагностируемой болезни (диагностируемого заболевания) у некоторой части субъектов и ее отсутствия у остальной части (у всех остальных).

2.Предполагается также, что имеет место строгая дихотомия: обследуемая популяция составлена исключительно из двух категорий субъектов – субъектов с данной болезнью и субъектов без данной болезни. Это подразумевает, что наличие или отсутствие данной болезни у любого случайно выбранного из данной популяции субъекта определяется практически безошибочно и однозначно. Для этого используется такое средство диагностики, которое считается эталонным, и его принято называть «золотым стандартом» или эталоном сравнения.

Из этой популяции извлекается случайная выборка субъектов. Если популяция однородная, а выборка случайная, то тогда выборка может считаться представительной (репрезентативной).

При этом, в силу действия закона больших чисел (ЗБЧ), чем больше объем такой выборки (n), тем более репрезентативной (представительной) она является. Это означает, что получаемые (вычисляемые) по данной выборке статистические оценки числовых характеристик (параметров, показателей) обследуемой (изучаемой) популяции по мере увеличения объема выборки будут все ближе сходиться (по вероятности) к значениям оцениваемых (неизвестных) характеристик (параметров) популяции. Например, в достаточно большой случайной выборке из однородной популяции доля субъектов с данным заболеванием (синдромом) может служить статистической оценкой распространённости этого заболевания.

Важно подчеркнуть, что при общепопуляционной (поперечно-срезовой) схеме из данной популяции отбирается случайная выборка субъектов без использования информации о наличии или отсутствии у них данной болезни.

Наличие или отсутствие болезни у отобранных субъектов определяется посредством применения эталонного средства ее диагностики уже после формирования исходной выборки.

Таким образом, после применения такого средства диагностики исходная случайная выборка субъектов подразделяется на две группы: субъекты с болезнью и без нее.